Лекція 7. Напруження при поперечному згинанні

При прямому поперечному згинанні в перерізі виникають поперечна сила , що викликає деформацію зсуву, та згинальний момент , що викликає деформацію згинання.

Нормальні напрження при чистому згинанні. Розглянемо випадок чистого згинання, коли в перерізі виникає тільки згинальний момент.

Покажемо стержень до деформації (рис. 7.1а) та після (рис. 7.1б) навантаження згинальними моментами .

Рис 7.1.

Спостерігаючи за деформацією ортогональної сітки, попередньо нанесеної на бічну поверхню балки до навантаження (рис.7.1а) і після (рис 7.1б), відзначимо, що подовжні лінії при чистому згинанні викривляються по дузі кола, контури поперечних перерізів залишаються плоскими, сліди яких перетинають подовжні лінії під прямими кутами. У стиснутій області (у даному випадку внизу) волокна коротшають, у зоні розтягання (угорі) подовжуються.

Існує подовжній шар, довжина якого при чистому згинанні залишається незмінною. Цей шар називається нейтральним. Зона розтягання та зона стискання в балці розділяються нейтральним шаром з радіусом кривизни .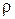

Відзначені обставини дозволяють ввести наступні гіпотези. При чистому згинанні виконується гіпотеза плоских перерізів. Усі поперечні перерізи стержня при чистому згинанні не викривляються, а лише повертаються один відносно одного навколо осі X. Подовжні волокна не давлять одне на одне. По ширині перерізу нормальні напруження не змінюються.

Логічно припустити, що в точках поперечного перерізу при чистому згинанні виникають тільки нормальні напруження, що приводять до інтегрального внутрішнього силового фактора – згинального моменту .

Через відсутність поперечних сил у напрямку осі Y, очевидно, що в точках перерізу дотичні напруження відсутні.

Розглянемо прямолінійний стержень довільного поперечного перерізу з віссю симетрії Y при чистому згинанні (рис.7.2а). В перерізі з координатою z застосуємо метод перерізів і одержимо: 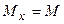(роис.7.2б).

В цьому перерізі момент виникає як сума моментів від розподілених внутрішніх зусиль (нормальних напружень 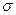). Виділимо елементарну площадку 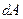з координатами (рис.7.2в). Нехай вісь Y – головна вісь, а вісь X збігається з нейтральним подовжнім шаром.

Задача про визначення внутрішніх зусиль відноситься до класу статично невизначених задач, тому далі застосовуємо схему рішення статично невизначених задач.

Рис.7.2.

Статична сторона задачі. Із шести рівнянь статичної рівноваги три рівняння виконуються тотожно. Елементарна сила в осьовому напрямку, що діє на площадку dA 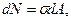результуюча сила 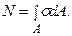Елементарний момент сили щодо осей X і Y запишеться як і 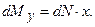Відповідно згинаючі моменти: ; .

Таким чином, умови статики приймуть вигляд:

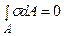; ; (7.1)

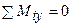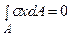; ; (7.2)

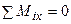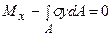; . (7.3)

Відзначимо невідомі: нормальне напруження 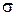– величина та закон розподілу; радіус кривизни r нейтрального шару; положення нейтрального шару.

Геометрична сторона задачі. Розглянемо деформацію елемента довжиною 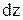. Нехай волокно 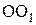збігається з нейтральним шаром, виділимо на відстані y від нього волокно 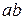(рис.7.3).

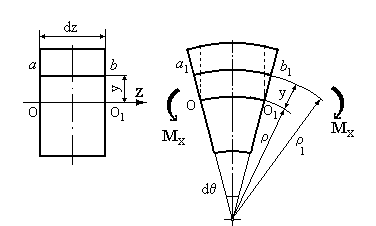
Рис.7.3.

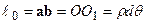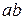
Початкова довжина волокна , тому що волокно не деформується. У процесі деформації довжина волокна складе довжину дуги: . Визначимо відносну деформац ію волокна . Так як подовжні волокна не давлять одне на одне, то, мабуть, така залежність справедлива для будь-якого волокна:

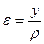. (7.4)

Це і є додаткова умова – рівняння спільності деформації при чистому згинанні.

Фізична сторона задачі. При чистому згинанні подовжні волокна піддаються розтяганню-стисканню, тому справедливий закон Гука для одновісного напруженого стану .

Після підстановки значення e з виразу (7.4) маємо:

. (7.5)

Підставляючи (7.5) послідовно в рівняння (7.1), (7.2), (7.3), одержимо наступне.

1. . Модуль подовжньої пружності для матеріалу ненульова константа; радіус кривизни r нейтрального шару є кінцевою величиною. Таким чином, статичний момент площі . Отже, нейтральний шар при чистому згинанні збігається з центральною віссю перерізу, тобто координата y відраховується від нейтральної лінії перерізу – геометричного місця точок, у яких нормальні напруження при згинанні дорівнюють нулю.

2. . Якщо відцентровий момент інерції щодо центральних осей дорівнює нулю, то ці осі є головними осями інерції. Таким чином, осі ХУ є головними осями інерції і нейтральна лінія є головною центральною віссю інерції, вона перпендикулярна площині дії навантаження.

3. 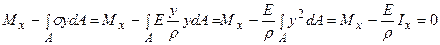, відкіля кривизна нейтрального подовжнього шару визначається виразом:

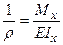, (7.6)

яке називається рівнянням Навье. Тут 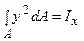– осьовий момент інерції перерізу, а EI_x – жорсткість стержня при згинанні.

Порівнюючи значення кривизни з рівнянь (7.5) і (7.6) одержимо:

.

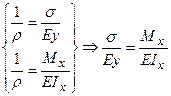Формула для визначення нормальних напружень прийме вигляд:

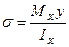. (7.7)

З отриманої формули випливає, що нормальні напруження 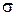по висоті перерізу змінюються лінійно, тому що згинальний момент та момент інерції I_x перерізу величини постійні. На рис 7.4 показані розподіли нормальних напружень по висоті для різних за формою перерізів.

Рис.7.4.

Максимальні напруження 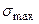виникають у найбільш віддалених точках від нейтральної лінії при , тобто 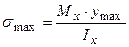, що повинні зіставлятися з допустимим напруженням .

Таким чином умова міцності при згинанні прийме вигляд:

. (7.8)

На практиці цей вигляд використовується для розрахунку перерізів, що мають одну вісь симетрії (рис. 7.4б). З обліком того, що 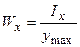- осьовий момент опору, то для перерізів із двома осями симетрії (рис. 7.4а) зручніше використовувати умову міцності при згинанні у вигляді:

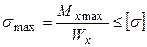. (7.9)

У випадку поперечного згинання, коли поперечна сила не дорівнює нулю, відбувається скривлення поперечних перерізів, і гіпотеза плоских перерізів не дотримується. Як показують дослідження, при відношенні довжини 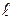стержня до висоти h поперечного перерізу (для більшості балок) можна вважати, що поперечний переріз практично не скривляється, тоді формула (7.7) для визначення нормальних напружень справедлива і при поперечному згинанні.

Приклад. Визначити розміри різних форм поперечних перерізів, якщо згинальний момент в перерізі кНм, допустиме напруження при згинанні 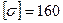МПа.

З умови міцності 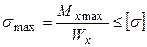осьовий момент опору перерізу 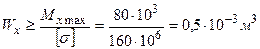= 500 см³. Далі проектуємо переріз (рис.7.5).

1. Прямокутний переріз (рис.7.5а), для якого повинне задаватися відношення 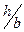(візьмемо ). Осьовий момент опору см³, відкіля 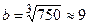см. Висота перерізу 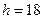см, площа поперечного перерізу см².

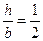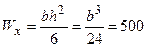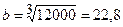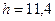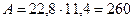2. Прямокутний переріз з відношенням (рис.7.5б). За аналогією: осьовий момент опору см³, відкіля см, см, см².

Рис.7.5.

3. Круглий суцільній переріз діаметром d (рис.7.5в). Осьовий момент опору 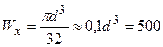см³, відкіля діаметр перерізу: 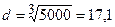см, площа 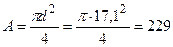см².

4. Кільцевий переріз (рис.7.5г). Задаються відношенням діаметрів 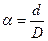, осьовий момент опору: см³. Нехай , тоді 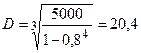см, см. Площа перерізу см².

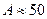5. Двотавровий переріз (рис.7.5д). За ДСТ 8239-72 підбираємо номер двотавра з найближчим більшим значенням осьового моменту опору до розрахункового. Так, для двотавра №30а: см³, см².

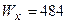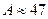6. Швелерний переріз (рис.7.5е). За ДСТ 8240-72 підбираємо номер швелера з найближчим більшим значенням осьового моменту опору до розрахункового. Так, для швелера №33 см³, см².

Узявши відношення окремих площ до площі раціонального поперечного перерізу (двотавр, швелер), одержимо коефіцієнт перевитрати матеріалу. Складемо таблицю (рис.7.5), з якої випливає, що самими раціональними є двотавровий і швелерний перерізи, y яких найменша площа поперечного перерізу та найменша витрата матеріалу.

Дотичні напруження при згинанні. Дія в перерізі поперечної сили викликає дотичні напруження t, що збігаються по напрямку з нею, по ширині перерізу не змінюються та визначаються за формулою Д.И.Журавського:

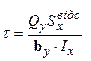, (7.10)

де 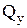- поперечна сила, що діє в перерізі; 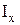- осьовий момент інерції перерізу щодо центральної осі X (нейтральної лінії); - ширина перерізу на тім рівні у від нейтральної лінії, де визначаються дотичні напруження; - абсолютне значення статичного моменту щодо центральної осі X частини перерізу, що лежить вище чи нижче того рівня, де визначаються дотичні напруження. Умова міцності по дотичним напруженням при поперечному згинанні записується у вигляді:

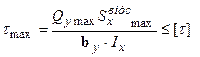. (7.11)

Таким чином, при прямому поперечному згинанні маємо умови міцності по нормальним 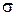та дотичним t напруженням. Основним вважається умова міцності по нормальним напруженням, а умова (7.11) по дотичним напруженням, як правило, перевіряється. Використання формули Д.И.Журавськогорозберемо на прикладах.

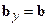Розподіл дотичних напружень для прямокутного перерізу. В перерізі діють згинаючий М_х момент і поперечна сила , спрямовані, як показано на рис.7.6. Поперечна сила , ширина перерізу та осьовий момент інерції конкретні постійні величини (рис.7.6). Таким чином, дотичні напруження змінюються за таким же законом, що і статичний момент відсіченої частини площі .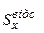

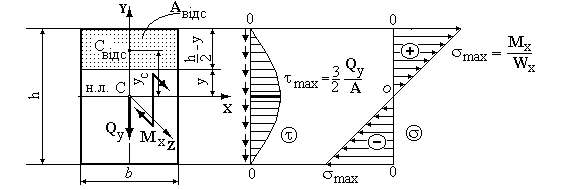
Рис.7.6.

Визначаємо дотичні напруження на рівні y. Площа відсіченої частини перерізу 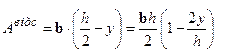, положення її центра ваги 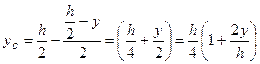. Статичний момент відсіченої частини площі:

Таким чином, дотичні напруження змінюються за законом квадратної параболи. Максимальні дотичні напруження виникають на нейтральній лінії, де нормальні напруження 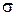дорівнюють нулю. Для визначення 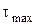необхідно обчислити статичний момент половини площі перерізу , і максимальні дотичні напруження визначаться як: 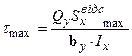. Для прямокутного перерізу , : .

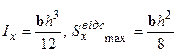Розподіл дотичних напружень для двотаврового перерізу. В перерізі діють згинальний М_х момент та поперечна сила , спрямовані, як показано на рис.7.7.

Рис.7.7.

Використовуючи вираз (7.10) для дотичних напружень, визначимо їхні значення в характерних точках.

Точка 1: , тому що (вище рівня 1 відсічена площа відсутня).

Точки 2,3. Ці точки мають однакову координату y, але належать полиці та стінці одночасно, тобто відповідають різній ширині b ₂= b; b ₃=d. Тому в місці переходу полки в стінку виникає скачок дотичних напружень.

Точка 2 (приналежна полиці): ;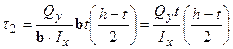

Точка 3 (приналежна стінці): ;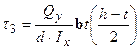

Точка 4: .

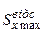- статичний момент щодо центральної осі половини площі перерізу, для стандартних профілів приведений у таблицях сортаменту. Зразковий графік розподілу дотичних напружень приведений на рис 7.7. Дійсний розподіл дотичних напружень трохи відрізняється від отриманого, тому що полиці мають ухили, а перехід від полиці до стінки здійснюється по радіусу кривини.

Дата добавления: 2015-06-28