Линии на плоскости

Решение.

Полярная система координат

Декартовая система координат дает удобный, но не единственный способ определения положения точек плоскости при помощи чисел.

Другой практически важной системой координат является полярная система координат. Полярная система координат задается точкой , которая называется полюсом, лучом 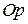, называемым полярной осью, и единичным вектором того же направления, что и луч .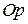

Числа r и j называются полярными координатами точки , пишут 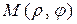, при этом r называют полярным радиусом, j - полярным углом.

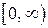Для получения всех точек плоскости достаточно полярный угол j ограничить промежутком (или ), а полярный радиус - . В этом случае каждой точке плоскости (кроме ) соответствует единственная пара чисел r и j, и обратно.

Установим связь между прямоугольными и полярными координатами.

, где .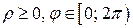

Если эти формулы разрешить относительно r и j, то получим следующие формулы:

.

Чтобы определить величину угла j, лучше использовать формулу , при этом устанавливается (по знакам и ) четверть, в которой лежит искомый угол, и учитывается, что (или ).

Пример 1.1. Построить точки, заданные полярными координатами:

.

Найти координаты точек в декартовой системе координат.

.

,

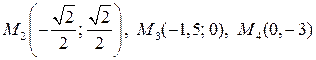Пример 1.2. Найти полярные координаты точки .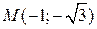

Решение. , следовательно, точка лежит в третьей четверти. Находим r и j:

,

Þ .

Учитывая, что , получаем 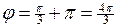. Таким образом, получаем точку .

,

Выше были введены координаты точек (декартовы или полярные) на плоскости, т.е. указан способ задания точек с помощью пары чисел. Метод координат в геометрии в том и состоит, что посредством координат точек геометрические объекты задают аналитически с помощью чисел, уравнений, неравенств или их систем. А это дает возможность при решении задач, доказательстве теорем использовать аналитические методы.

Метод координат на плоскости используется в геометрии для изучения линий. Линия (или кривая) плоскости задается как множество точек, обладающих некоторым только им присущим геометрическим свойством. Например, прямая, окружность, парабола, синусоида и т.д.

Линию (кривую) на плоскости можно задать:

1) уравнением в декартовой системе ;

2) уравнением в полярной системе координат;

3) параметрически;

4) векторным уравнением.

Уравнением линии (или кривой) на плоскости называется такое уравнение с двумя переменными, которому удовлетворяют координаты и каждой точки линии и не удовлетворяют координаты любой точки, не лежащей на этой линии.

Так, для того чтобы установить, лежит ли точка на данной линии, достаточно проверить (не прибегая к геометрическим построениям), удовлетворяют ли координаты точки уравнению этой линии в выбранной системе координат.

Задача о нахождении точек пересечения двух линий, заданных уравнениями и , сводится к отысканию точек, координаты которых удовлетворяют уравнениям обеих линий, т.е. сводится к решению системы двух уравнений с двумя неизвестными:

.

Если эта система не имеет действительных решений, то линии не пересекаются.

Уравнение называется уравнением данной линии в полярной системе координат, если координаты любой точки, лежащей на этой линии, и только они, удовлетворяют этому уравнению.

Линию на плоскости можно задать параметрически при помощи двух уравнений:

,

где и - координаты произвольной точки 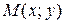, лежащей на данной линии, а - переменная, называемая параметром; параметр определяет положение точки 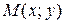на плоскости. Если параметр изменяется, то точка на плоскости перемещается, описывая данную линию. Система из двух уравнений называется параметрическими уравнениями линии.

Чтобы перейти от параметрических уравнений линии к уравнению вида , надо каким-либо способом из двух уравнений исключить параметр . Однако, заметим, такой переход не всегда целесообразен и не всегда возможен.

Пример 1.3. Построить линию, которая задана параметрически:

.

Составить уравнение линии в декартовой и полярной системе координат

Дата добавления: 2017-01-14