
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Общее уравнение прямой
|
|
|
|
Решение.

В первом уравнение выразим  через
через  , и подставим во второе уравнение:
, и подставим во второе уравнение:
 Þ
Þ  или
или
 .
.
В полученное уравнение в декартовой системе координат подставляем  ,
, 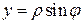 , и выражаем
, и выражаем  :
:
 ;
;
 - уравнение данной прямой в полярной системе координат.
- уравнение данной прямой в полярной системе координат.
,
Пример 1.4. Составить уравнение окружности с центром в начале координат  и радиусом
и радиусом  : в декартовой, в полярной системе координат и параметрически.
: в декартовой, в полярной системе координат и параметрически.
Решение. Напомним, что окружность радиуса  есть множество всех точек плоскости, удаленных на расстоянии
есть множество всех точек плоскости, удаленных на расстоянии  от некоторой фиксированной точки
от некоторой фиксированной точки  (центра окружности).
(центра окружности).

В уравнение окружности в декартовой системе координат вместо  и
и  подставляем
подставляем  ,
, 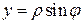 , и выражаем
, и выражаем  :
:
 ;
;
 ;
;
 - уравнение окружности в полярной системе координат.
- уравнение окружности в полярной системе координат.
В качестве параметра  можно взять угол поворота точки
можно взять угол поворота точки  при движении по окружности. Тогда
при движении по окружности. Тогда
 - параметрические уравнения окружности.,
- параметрические уравнения окружности.,
 Линию на плоскости можно задать векторным уравнением
Линию на плоскости можно задать векторным уравнением 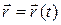 , где
, где  - скалярный переменный параметр. Каждому значению
- скалярный переменный параметр. Каждому значению 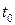 соответствует определенный вектор
соответствует определенный вектор  плоскости. При изменении параметра
плоскости. При изменении параметра  конец вектора
конец вектора 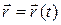 описывает
описывает

Векторное уравнение и параметрические уравнения линии имеют механический смысл. Если точка перемещается на плоскости, то указанные уравнения называются уравнениями движения, а линии – траекторией точки, параметр  при этом есть время.
при этом есть время.
В аналитической геометрии на плоскости возникают две основные задачи:
1) зная геометрические свойства кривой, найти ее уравнение;
2) зная уравнение кривой, изучить ее форму и свойства.
Приведем примеры некоторых кривых, и укажем их уравнения:









2. УРАВНЕНИЕ ПРЯМОЙ НА ПЛОСКОСТИ
Простейшей из линий является прямая. Разным способам задания прямой соответствуют в прямоугольной системе координат разные виды ее уравнений.
Положение прямой  на плоскости вполне определено, если известны точка
на плоскости вполне определено, если известны точка  , через которую она проходит, и ненулевой вектор
, через которую она проходит, и ненулевой вектор  , перпендикулярный к этой прямой.
, перпендикулярный к этой прямой.
Постановка задачи: Составить уравнение прямой, проходящей через точку  , и перпендикулярную вектору
, и перпендикулярную вектору  . Вектор
. Вектор  называется нормальным вектором прямой.
называется нормальным вектором прямой.

 . (2.1)
. (2.1)
Соотношение (2.1) удовлетворяет координатам тех и только тех точек плоскости  , которые принадлежат прямой
, которые принадлежат прямой  . Формула (2.1) называется уравнением прямой с нормальным вектором
. Формула (2.1) называется уравнением прямой с нормальным вектором  и проходящей через точку
и проходящей через точку  .
.
Раскрыв скобки в уравнении (2.1), получим
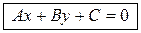 , (2.2)
, (2.2)
где 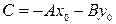 . Уравнение (2.2) называется общим уравнением прямой с нормальным вектором
. Уравнение (2.2) называется общим уравнением прямой с нормальным вектором  .
.
Общее уравнение прямой (2.2) называется полным, если все его коэффициенты 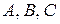 отличны от нуля. Если же хотя бы один из них равен нулю, то уравнение называется неполным. Рассмотрим возможные случаи неполных уравнений:
отличны от нуля. Если же хотя бы один из них равен нулю, то уравнение называется неполным. Рассмотрим возможные случаи неполных уравнений:
1) при  уравнение
уравнение  определяет прямую, проходящую через начала координат;
определяет прямую, проходящую через начала координат;
2) при  уравнение
уравнение 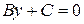 Û
Û  определяет прямую, перпендикулярную к вектору
определяет прямую, перпендикулярную к вектору  и параллельную оси
и параллельную оси  . Если
. Если  , то уравнение
, то уравнение  определяет ось
определяет ось  ;
;
3) при 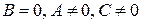 уравнение
уравнение 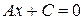 Û
Û 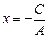 определяет прямую, перпендикулярную к вектору
определяет прямую, перпендикулярную к вектору  и параллельную оси
и параллельную оси  . Если
. Если  , то уравнение
, то уравнение  определяет ось
определяет ось  .
.
|
|
|
|
|
Дата добавления: 2017-01-14; Просмотров: 227; Нарушение авторских прав?; Мы поможем в написании вашей работы!