Решение типовых задач. Задача 3.1. Система состоит из трех устройств

Задача 3.1. Система состоит из трех устройств. Интенсивность отказов типового устройства равна λ₁=0,16·10^-3 l/чac=const. Интенсивности отказов двух электромеханических устройств линейно зависят от времени и определяются следующими формулами: λ₂=0,23·10^-4 t 1/час, λз=0,06·10^-6 t^2,6 1/час. Необходимо рассчитать вероятность безотказной работы изделия в течение 100 час.

Решение. На основании формулы (3.3) имеем:

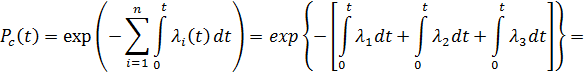
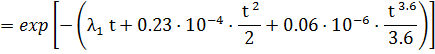
Для t=100 час имеем:

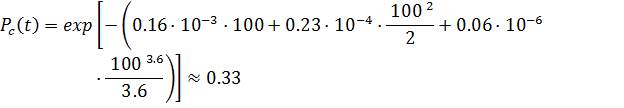
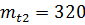Задача 3.2. Система состоит из трех блоков, среднее время безотказной работы которых равно: час; час; 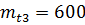час. Для блоков справедлив экспоненциальный закон надежности. Требуется определить среднее время безотказной работы системы.

Решение. Воспользовавшись формулой (3.17) получим:

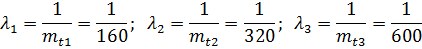
Здесь λ_i - интенсивность отказов i -го блока. На основании формулы (3.11) имеем:

λ_с = λ₁ + λ₂ + λ₃ = .

Здесь λ_с - интенсивность отказов системы. На основании формулы (3.16) получим:

Задача 3.3. Система состоит из 12600 элементов, средняя интенсивность отказов которых λ_ср=0,32 · 10^-6 1/час. Требуется определить P_c(t), q_c(t), fc(t), m_tc, для t =50 час.

Здесь Pc(t) - безотказной работы системы в течение времени t;

q_c(t) - вероятность отказа системы в течение времени t;

f_c(t) - частота отказов или плотность вероятности времени Т безотказной работы системы;

m_tc - среднее время безотказной работы системы.

Решение. Интенсивность отказов системы по формуле (3.11) будет

.

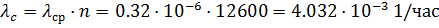Из (3.13) имеем:

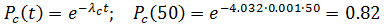
Из (3.15) получим:

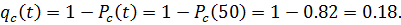
Из (3.14) имеем:

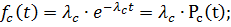
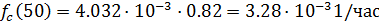
Из (3.16) получим:

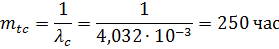
Задача 3.4. Система состоит из двух устройств. Вероятности безотказной работы каждого из них в течение времени t =100 час равны: Р₁(100)=0,95; Р₂(100)=0,97. Справедлив экспоненциальный закон надежности. Необходимо найти среднее время безотказной работы системы.

Решение. Найдем вероятность безотказной работы изделия:

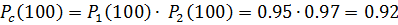
Найдем интенсивность отказов изделия, воспользовавшись формулой:

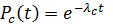или 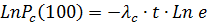, откуда =

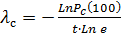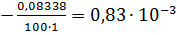= , тогда .

Задача 3.5. Вероятность безотказной работы одного элемента в течение времени t равна P(t)=0,9997. Требуется определить вероятность безотказной работы системы, состоящей из n = 100 таких же элементов.

Решение. Вероятность безотказной работы системы равна:

Вероятность Pc(t) близка к единице, поэтому для ее вычисления воспользуемся формулой (3.18). В нашем случае q(t)=l-P(t)=l-0,9997=0,0003.

Тогда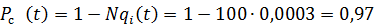

Задача.3.6.Вероятность безотказной работы системы в течение времени t равна Pc(t)=0,95. Система состоит из n=120 равнонадежных элементов. Необходимо найти вероятность безотказной работы элемента.

Решение. Очевидно, что вероятность безотказной работы элемента будет

Так как P(t) близка к единице, то вычисления P(t) удобно выполнить по формуле (3.18). В нашем случае 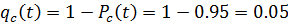, тогда:

Задача 3.7. Система состоит из 12600 элементов, средняя интенсивность отказов которых λср =0,32·10^-6 1/час. Необходимо определить вероятность безотказной работы в течение t = 50 час.

Решение. Интенсивность отказов системы по формуле (3.11) будет:

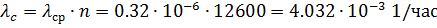
Тогда на основании (3.13) имеем:

Дата добавления: 2015-07-13