Аналитическая геометрия на плоскости

Контрольная работа №1

ЗАДАЧИ ДЛЯ КОНТРОЛЬНЫХ РАБОТ

Астрахань 2008

ПО МАТЕМАТИКЕ

для студентов, обучающихся на заочном отделении

МЕХАНИЧЕСКОГО ФАКУЛЬТЕТА

Автор:	Ассистент каф. «Математика в инженерном образовании» Галяув Е.Р. ст. преподаватель каф. «Математика в инженерном образовании» Франгулова Е.В.
Рецензент:	к.п.н., доцент Мамаева Н.А. каф. «Математика в инженерном образовании»

Методическое пособие рассмотрено и рекомендовано к печати кафедрой «Высшая математика» " 04 " октября 2008г.,

протокол № 2.

ПРЕДИСЛОВИЕ

Сборник контрольных заданий предназначен для студентов заочного отделения Механического факультета. Задачи, представленные в сборнике, подобраны в соответствии с действующей программой по курсу математики для инженерно-технических специальностей и охватывают разделы: линейная алгебра, аналитическая геометрия на плоскости и в пространстве, введение в анализ, дифференциальное исчисление функции одной и нескольких переменных, ряды (числовые, степенные, Фурье), ТФКП, операционное исчисление, вариационное исчисление, теория вероятности, математическая статистика. Каждый раздел содержит по десять вариантов заданий.

Студент первого курса выполняет контрольные работы №1, №2 и №3, второго курса - №4 и №5, третьего курса - №6. Номер варианта задания соответствует последней цифре номера зачетной книжке студента.

В задачах 1-10 даются координаты вершин некоторого треугольника . Требуется:

1) вычислить длину стороны ;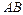

2) составить уравнение линии ;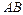

3)составить уравнение высоты, проведенной из вершины ;

4) вычислить расстояние от вершины 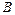до стороны ;

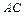5) вычислить угол 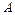(в радианах с точностью до двух знаков).

1. , , .

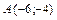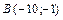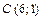2. , , .

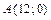3. , , .

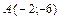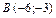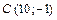4. , , .

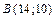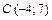5. , , .

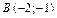6. , , .

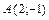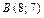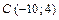7. , , .

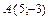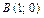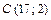8. , , .

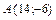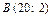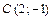9. , , .

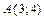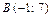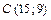10. , , .

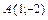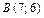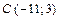11. Найти уравнение диагонали параллелограмма, не проходящей через точку пересечения его сторон 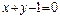и 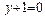, если известно, что диагонали параллелограмма пересекаются в точке .

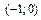12. На прямой 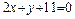найти точку, равноудаленную от двух данных точек 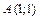и .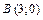

13. Найти координаты точки, симметричной точке 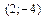относительно прямой .

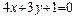14. Вычислить координаты центра окружности, описанной около треугольника с вершинами , , .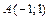

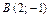15. Составить уравнение прямой, проходящей через точку 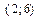и образующей с осями координат треугольник, который находится во второй четверти и имеет площадь 3 кв. ед.

16. Составить уравнение прямой, проходящей через точку 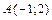так, что середина ее отрезка, заключенного между параллельными прямым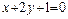и и 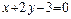, лежит на прямой .

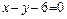17. Даны уравнения двух сторон треугольника 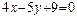и 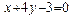. Найти уравнение третьей стороны, если известно, что медианы этого треугольника пересекаются в точке .

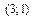18. Вычислить координаты вершин ромба, если известны уравнения двух его сторон 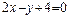и 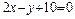, и уравнение одной из его диагоналей .

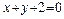19. Составить уравнения сторон треугольника, есл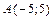и и 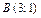- две его вершины, а - точка пересечения его высот.

20. Дано 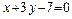- уравнение одной из сторон квадрата и 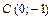- точка пересечения остальных трех сторон этого квадрата.

21. Составить уравнение эллипса, у которого эксцентриситет равен 0,8, а фокальные радиусы одной из его точек равны 2 и 3, полагая, что большая ось эллипса совпадает с осью абсцисс, его центр – с началом координат

22. На гиперболе 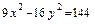найти точки, расстояние которых от левого фокуса вдвое меньше, чем от правого.

23. Найти параметр параболы и уравнение ее директрисы, если известно, что эта парабола проходит через точки пересечения прямой 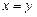с окружностью .

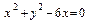24. На эллипсе найти точки, в которых фокальные радиусы были бы взаимно перпендикулярны.

25. Фокусы гиперболы находятся в точках 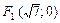и . Гипербола проходит через точку 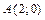. Найти уравнения ее асимптот и угол между ними.

26. Составить уравнение геометрического места точек, равноудаленных от точки 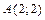и от оси абсцисс.

27. Составить уравнение геометрического места точек, каждая из которых находится вдвое дальше от точки 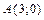, чем от оси ординат.

28. Составить уравнение геометрического места точек, для которых отношение расстояния до начала координат к расстоянию до прямой 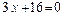равно 0,6.

29. Составить уравнение геометрического места точек, каждая из которых находится вдвое ближе к точке 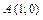, чем к точке .

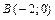30. Составить уравнение геометрического места центров окружностей, касающихся оси абсцисс и проходящих через точку .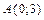

Дата добавления: 2015-08-31