КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Нескольких переменных
|
|
|
|
Дифференциальное исчисление функций
Ряды
Контрольная работа №4
В задачах 311-320 исследовать сходимость числового ряда.
311. 
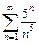
| 312. 
|
313. 
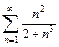
| 314.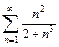
|
315. 
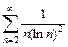
| 316. 
|
317. 
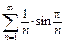
| 318.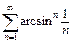 
|
319. 
| 320. 
|
В задачах 321-330 найти интервал сходимости степенного ряда.
321. 
| 322.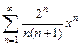 
|
323. 
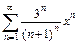
| 324. 
|
325. 
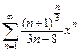
| 326. 
|
327. 
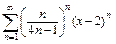
| 328.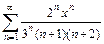 
|
329. 
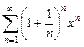
| 330. 
|
В задачах 331-340 разложить данную функцию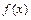 
в ряд Фурье в указанном интервале:
331. 
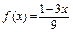в интервале 
.
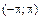332. 
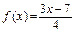в интервале 
.
333. 
в интервале .
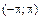334. 
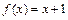в интервале 
.
335. 
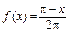в интервале 
.
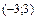336. 
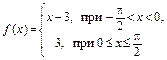в интервале 
.
337. 
в интервале 
.
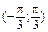338. 
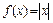в интервале .
339. 
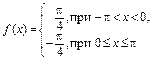в интервале .
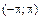340. 
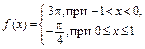в интервале 
.
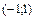В задачах 341-350 вычислить определенный интеграл с точностью до 0,001. С этой целью подынтегральную функцию следует разложить в ряд, который затем почленно проинтегрировать.
341. 
| 342. 
|
343. 
| 344.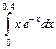 
|
345. 
| 346.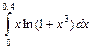 
|
347. 
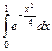
| 348.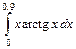 
|
349. 
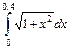
| 350.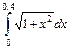
|
В задачах 351-360 найти три первых, отличных от нуля, члена разложения в степенной ряд интеграла 
дифференциального уравнения, удовлетворяющего заданному начальному условию.
351. 
.
352. 
.
353. 
.
354. 
.
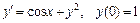355. 
.
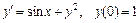356. 
.
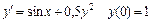357. 
.
358. 
.
359. 
.
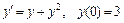360. 
.
361. Дана функция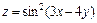 
. Показать, что 
.
362. Дана функция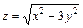 
. Показать, что 
.
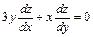363. Дана функция 
. Показать, что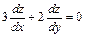 
.
364. Дана функция 
. Показать, что 
.
365. Дана функция 
. Показать, что 
.
366. Дана функция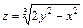 
. Показать, что 
.
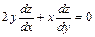367. Дана функция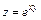 
. Показать, что 
.
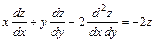368. Дана функция 
, Показать, что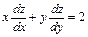 
.
369. Дана функция 
. Показать, что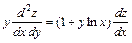 
.
370. Дана функция 
. Показать, что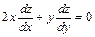 
.
В задачах 371-380 дана функция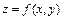 
и две точки 
и 
. Требуется:
1) вычислить значение 
функции в точке 
;
2) вычислить приближенное значение 
функции в точке , исходя из значения 
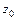функции в точке 
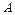, заменив приращение функций при переходе от точки 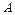к точке дифференциалом, и оценить в процентах относительную погрешность, возникающую при замене приращения функции дифференциалом;
3) составить уравнение касательной плоскости к поверхности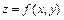 
в точке 
и проверить, лежит ли точка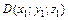 
в этой плоскости.
371. 
, 
.
372. 
, 
.
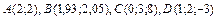373. 
, 
.
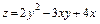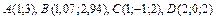374. 
, 
.
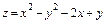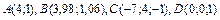375. 
, 
.
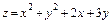376. 
, 
.
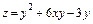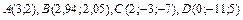377. 
, 
.
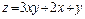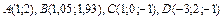378. 
, 
.
379. 
, 
.
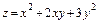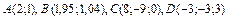380. 
, 
.
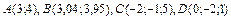В задачах 381-390 требуется найти наименьшее и наибольшее значения функции в замкнутой области.
381. 
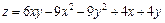в прямоугольнике 
, 
.
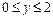382. 
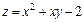в области, ограниченной параболой 
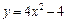и осью 
.
383. 
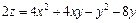в треугольнике, ограниченном линиями 
.
384. 
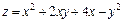в треугольнике, ограниченном прямым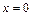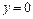и 
, 
и 
.
385. 
в квадрате 
.
386. 
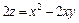в области, ограниченной параболой 
и прямой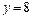 
.
387. 
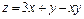в треугольнике, ограниченном прямыми 
, 
и .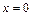
388. 
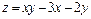в квадрате 
.
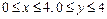389. 
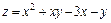в прямоугольнике 
.
390. 
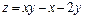в треугольнике, ограниченном прямыми , 
и .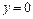
В задачах 391-400 даны: функция 
, точка 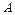и вектор 
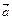. Требуется найти:
1) 
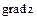в точке ;
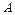2) производную в точке 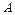по направлению вектора .
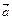391. 
.
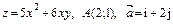392. 
.
393. 
.
394. 
.
395. 
.
396. 
.
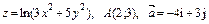397. 
.
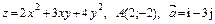398. 
.
399. 
.
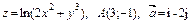400. 
.
|
|
|
|
|
Дата добавления: 2015-08-31; Просмотров: 276; Нарушение авторских прав?; Мы поможем в написании вашей работы!