Методы теории принятия решений

Тема 7. Методы прогнозирования в экономическом анализе

7.1. Методы теории принятия решений

7.2. Методы ситуационного анализа и прогнозирования

7.3. Неформализованные методы экономического анализа

В данную группу методов входят: метод построения дерева решений; метод оптимального линейного программирования; метод теории игр. Рассмотрим каждый из них.

Метод «дерево решений» является полезным в решении задач классификации явлений и прогнозирования с ограниченным количеством вариантов и представляет собой постановку и решение задачи в виде иерархической последовательности действий. Суть метода состоит в следующем: строят все варианты решений, то есть дерево решений; по ветвям дерева соотносят субъективные и объективные оценки возможных событий, при этом учитывают вероятности возможных исходов; оценивают каждый путь и выбирают тот путь, по которому можно получить наибольшую прибыль.

Логическую схему проведения анализа рассмотрим на конкретном примере: руководство предприятия должно принять решение о приобретении одного из четырёх станков, имеющих разные экономические характеристики – цену, производительность. Исходные данный для построения дерева решений представлены в таблице 7.3.

Таблица 7.1 – Исходные данные для построения дерева решений
Вид станка	Постоянные затраты, руб.	Операционный доход не единицу продукции, руб.
Станок №1
Станок №2
Станок №3
Станок №4

Необходимо отдать предпочтение либо более экономичному варианту, либо варианту, обеспечивающему больший доход на единицу продукции, но вместе с тем более дорогому и требующему относительно больших накладных расходов.

Построение дерева решений осуществляется в несколько этапов.

На первом этапе выбирается критерий – максимизация математического ожидания прибыли.

На втором этапе определяется набор возможных решений для рассмотрения и анализа из следующих вариантов:b₁, b_2,b_3, b_4.

На третьем этапе оцениваются возможные результаты и их вероятности (носят случайный характер). Так, например, аналитик оценивает возможные варианты годового спроса на продукцию и соответствующие им вероятности:

Х₁ = 1200 единиц с вероятностью 0,4; Х₂ = 2000 единиц с вероятностью 0,6.

На четвёртом этапе даётся оценка математического ожидания возможного дохода. Построение дерева решений представлено в таблице 7.2.

Таблица 7.2 – Построение дерева решений

Альтернативные варианты приобретения станков	Станки	Расчёт ожидаемой прибыли по каждому варианту ожидаемого спроса	Ожидаемая прибыль	Математическое ожидание по проекту
Станок №1	20*1200 - 15000
20*2000-15000
Станок №2	24*1200-21000
24*2000-21000
Станок №3	33*1200-38000
33*2000-38000
Станок №4	35*1200-55000	-13000
35000*2000-55000

Расчёт математического ожидания (Е) по каждому проекту с учётом вероятности наступления события представлен ниже:

Е(R_b1) = 900 * 0,4 + 25 000 * 0,6 = 18 600 руб;

Е(R_b2) = 7 800 * 0,4 + 27 000 * 0,6 = 19 320 руб;

Е(R_b3) = 1 600 * 0,4 + 28 000 * 0,6 = 17 440 руб;

Е(R_b4) = -13 000 * 0,4 + 15 000 * 0,6 = 3 800 руб.

Расчёты показывают, что вариант с приобретением станка №2 является экономически более целесообразным. Необходимо отметить, что метод построения дерева решений успешно может быть использован в различных областях деятельности: банковском деле, при составлении бюджета капиталовложений, при анализе на рынке ценных бумаг, управленческом учёте.

Методы оптимального линейного программирования. Линейное программирование – это направление математического программирования. Оно изучает методы решения экстремальных задач, характеризующиеся линейной зависимостью между переменными и линейным критерием. Необходимым условием постановки задачи линейного программирования являются ограничения на величину спроса, ресурсы, производственную мощность и другие производственные факторы. Методы линейного программирования, особенностью которых является использование сложного экономико-математического аппарата, нашли широкое применение при планировании деятельности, что позволяет находить оптимальные параметры выпуска и варианты наилучшего использования имеющихся ресурсов. Суть метода линейного программирования – поиск максимума или минимума целевой функции при имеющихся ограничениях.

Математические исследования отдельных экономических проблем проводились ещё в 19 веке. В 1920 годы был разработан межотраслевой баланс, послуживший толчком в деле создания и исследования математических моделей. Экономист и статистик В.В. Леонтьев разработал межотраслевую модель производства и распределения продукции. В статье «Баланс народного хозяйства» ученый показал, что коэффициенты, выражающие связи между отраслями экономики, достаточно стабильны и их можно прогнозировать. В 1939 году Л.В. Канторович заложил основы линейного программирования, опубликовав работу «Математические методы организации и планирования производства», в которой сформулировал новый класс экстремальных задач с ограничениями и разработал эффективный метод их решения. Термин «программирование», понимаемый в смысле планирования, был предложен в середине 1940-х годов Джорджем Данцигом, одним из основателей линейного программирования, ещё до того, как компьютеры были использованы для решения линейных задач оптимизации. В 1949 году им был разработал симплекс-метод - эффективный метод линейного программирования.

Использование данного метода рассмотрим на искомом примере.

Предприятие производит две марки кофе – «А» и «Б». Отпускная цена кофе марки «А» - 600 руб. за килограмм, марки «Б» - 500 руб. за килограмм. При изготовлении кофейных смесей разных марок используют кофейные зёрна двух сортов. В состав кофе марки «А» входит 70% сырья 1-го сорта и 30% сырья второго сорта. В состав кофе марки «Б» входит 20% сырья 1-го сорта и 80% сырья второго сорта. Стоимость сырья 1-го сорта составляет 380 руб/кг, 2-го сорта – 240 руб/кг.

Имеющиеся ограничения:

- для изготовления обоих сортов кофе используется одно и то же оборудование, его производительность в год составляет 300 т продукции;

- на закупку сырья может в год быть потрачено не более 90000 руб.;

Необходимо определить оптимальный годовой объём производства кофе обеих марок, который обеспечит максимальную выручку от реализации.

Этапы и последовательность решения задачи:

1. Допустим, что оптимальный объём производства кофе в год марки «А» составит х тонн, марки «Б» - у тонн, тогда выручка от реализации составит (600х + 500у) тыс. руб. Необходимо найти такую комбинацию (х,у), которая позволит обеспечить максимум этой функции: 600х + 500у →max;

2. Необходимо рассчитать себестоимость сырья для производства одного килограмма кофе марки «А» и одного килограмма кофе марки «Б»:

- марки «А»: 0,7 * 380 + 0,3 * 240 = 266 + 72 = 338 руб.

- марки «Б»: 0,2 * 380 + 0,8 * 240 = 76 + 192 = 268 руб.

3. Ограничение по мощности оборудования составит:

х + у ≤ 300;

4. Ограничения по финансированию составят:

338 * х + 268 * у ≤ 90000;

5. Полная формулировка задачи линейного программирования:

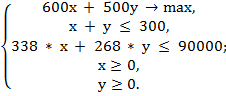
Решение системы уравнений:

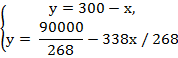
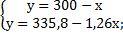
300 – х = 335,8 – 1,26х;

х = 138;

у = 300 – 138 = 162.

Исходные данные и решение задачи по выбору оптимального объёма производства методом линейного программирования представлены в таблице 7.3.

Типичными примерами применения модели линейного программирования являются: разработка рационального плана использования сырья (оптимальный раскрой ткани, стальных и деревянных листов и т.д), планирование ассортимента изделий; регулирование запасов (определение оптимального сочетания видов запасов на складе); оптимальное размещение производственных мощностей; составление графиков производства, минимизирующих общие издержки в связи с изменением ставки процента; планирование распределения продукции. С помощью метода оптимального линейного программирования решаются также задачи составления расписания; составление оптимального плана по перевозке грузов и др.

Таблица 7.3 – Решение задачи определения оптимального объема производства, обеспечивающего максимальную выручку методом линейного программирования

Наименование продукта	Цена за 1 кг	Оптимальный объём производства	Состав кофе, %	Себестоимость
1-й сорт/цена	2-й сорт/цена	0,7*380+0,3*240
		0,2*380+0,8*240
Кофе, сорт "А"		х
Кофе, сорт "А=Б"		у
Оптимальный объём	60х+50у
Закупка сырья в год не более 90000 тыс. руб.	338*х+268*у ≤ 90000
Ограничения по объёму выпуска (производственной мощности)	х+у ≤ 300
Максимальный объём сорта "А" с учётом финансового ограничения 90000/338	266,3
Максимальный объём сорта "Б" с учётом финансового ограничения 90000/268	335,8
Формулировка задачи линейного программирования	у=300-х
у=335,8-1,26х
Оптимальный объём производства кофе сорта "А"
Оптимальный объём производства кофе сорта "Б"
Именно такое соотношение объёмов выпуска кофе соротв "А" и "Б" позволит предприятию получить максимальный объём выручки при существующих технологических и финансовых ограничениях

Метод теории игр. Изучая методы линейного программирования, можно заметить, что решение принималось одним человеком при отсутствии конфликтных ситуаций: были известны целевая функция, ограничения по производственным и финансовым ресурсам и способы их использования. Однако, при решении экономических задач часто анализируются ситуации, в которых сталкиваются интересы двух или более конкурирующих сторон. Такие ситуации называются конфликтными. Теорией конфликтных ситуаций является теория игр – совокупность способов и методов разрешения конфликта между участниками в различных процессах и явлениях. Исследуя конфликтные ситуации, теория игр позволяет на их основе разрабатывать рекомендации по наиболее рациональному образу действия каждого из участников в ходе конфликтной ситуации. Методы теории игр применяются в отношении многократно повторяющихся конфликтных ситуаций; если конфликтная ситуация реализуется однократно или ограниченное число раз, то рекомендации теории игр теряют смысл.

Оптимальные решения в математическом моделировании предлагались ещё в 18 веке. В 19 веке А. Курно и Ж. Бертраном рассматривались задачи ценообразования в условиях олигополии, ставшие впоследствии хрестоматийными примерами теории игр. Э.Ласкер, Э.Цермело и,Э. Борель в начале 20 века выдвигают идею математической теории конфликта интересов. Математическая теория игр берёт своё начало из неоклассической экономики. В 1944 году Джон фон Нейман и Оскар Моргенштерн в книге «Теория игр и экономическое поведение» впервые изложили математические аспекты и приложения теории. Серьёзный вклад в развитие теории игр внесли работы Дж. Нэша –лауреата Нобелевской премии. Им были пересмотрены математические инструменты экономического моделирования. Он показал, что классический подход к конкуренции А. Смита, когда каждый сам за себя, не оптимален – более оптимальны стратегии, когда каждый старается сделать лучше для себя, делая лучше для других.

С 1950-х гг. методы теории игр начинают применять не только в экономике, но также в кибернетике, биологии, антропологии, технике. В 1960-1970 гг. интерес к теории игр угасает, а с середины 1980-х гг. начинается активное применение теории игр в экономике и менеджменте. За последние годы интерес значительно растёт.

Большим вкладом в применение теории игр стала работа Томаса Шеллинга «Стратегия конфликта», в которой нобелевский лауреат по экономике 2005 г. рассматривает различные «стратегии» поведения участников конфликта.

Математическая теория игр бурно развивается, однако её математический аппарат является затратным. Математический аппарат теории игр применяют для оправданных задач: политика, экономика монополий и распределение рыночной власти.

Примером применения теории игр может быть ситуация, в которой участвуют покупатель и продавец. Конфликт между сторонами может возникнуть из-за различных целей: продавцу выгоднее продать товар по высокой цене, покупателю выгодно купить товар по низкой цене. В этом случае интересы покупателя и продавца антагонистические.

На промышленных предприятиях теория игр может использоваться, например, создании рациональных запасов сырья, материалов, полуфабрикатов. В данном случае противоборствуют две тенденции: увеличение запасов, в том числе страховых, гарантирующее бесперебойную работу предприятия, и сокращение запасов в целях минимизации затрат на их хранение. Математические модели управления запасами позволяют найти оптимальный уровень запасов, минимизирующий совокупные затраты по закупке и хранению запасов на предприятии (модель Уилсона), то есть в качестве критерия оптимальности можно принять min издержек обращения.

Чем больше партия заказа и реже производится поставка товаров, тем ниже сумма затрат по завозу товаров. Сумма затрат по завозу определяется по формуле:

L_п.з = 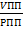* Ц _рз,

где L_п.з – затраты по поставке запасов (товаров, материалов и т.д.);

VПП – годовой объём потребности запасов;

РПП – средний размер одной партии поставки;

Ц _рз – средняя стоимость размещения одного заказа (затраты на завоз – закупку и поставку).

Из формулы видно, что при неизменном VПП и Ц _рз с ростом РПП сумма затрат на размещение заказа уменьшается, и наоборот, из чего следует, что предприятию выгоднее завозить товары большими партиями.

С другой стороны, большой размер одной партии вызывает соответствующий рост затрат по хранению товаров на складе, так как увеличивается размер запаса в днях. Сумма затрат по хранению товаров определяется по формуле:

L_хр.з = 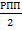* С _{хр з},

где L_хр.з – затраты по хранению запасов (товаров, материалов и т.д.);

С _{хр з} – средняя стоимость хранения единицы товара.

Из формулы видно, что при снижении среднего размера одной партии поставки (РПП) и при неизменной стоимости хранения единицы товара (С _{хр з}) сумма затрат по хранению товаров на складе минимизируется.

Модель экономически обоснованного заказа (EOQ) позволяет оптимизировать пропорции между двумя группами затрат таким образом, чтобы была минимальной общая сумма затрат.

Математическая модель EOQ выражается формулой:

EOQ = ,

где EOQ – оптимальный средний размер партии поставки.

Любое отклонение от оптимальной партии поставки вызовет увеличение данных расходов. Чтобы снизить вероятность нехватки запасов, необходимо иметь резервный запас, что повлечёт дополнительные затраты на хранение. Затраты по поставке и хранению запасов в этом случае рассчитываются по формуле:

L_min = Ц _рз * 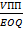+ С _хрз * ,

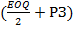где РЗ – резервный запас.

Рассмотрим пример определения оптимального размера заказа: годовая потребность в ткани у предприятия составляет 450000 м. Стоимость размещения одного заказа составляет 10000 руб., затраты по хранению единицы товара составляют 100 руб. Время доставки заказа – 5 дней. Предприятие работает 300 дней в году. Необходимо определить:

- оптимальный размер одного заказа;

- количество заказов в год (q);

- интервал поставки (N);

- уровень запаса, при котором необходимо сделать очередной заказ;

- минимальную сумму затрат по завозу и хранению;

- чувствительность данных показателей к изменению спроса и соответственно годовой потребности в ткани до 600 000 м;

- общую сумму затрат при условии заказа в размере 20000 м и 40000 м;

- затраты по завозу и хранению при условии необходимости резервного запаса в 3000 м.

Исходные данные и решение задачи представлено в таблице 7.4.

Таблица 7.4 – Определение оптимального размера заказа

Показатель	Условное обозначение	Значение показателя
Годовая потребность в ткани, м	VПП
Стоимость размещения одного заказа, руб.	Цр.з.
Стоимость хранения единицы товара, руб.	С хр.з.
Время доставки заказа, дней	t
Количество рабочих дней в году	Д
Оптимальный средний размер партии поставки, м EOQ =
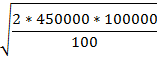
Количество заказов в год Q = VПП / EOQ 450000/30000
Интервал поставки, дней N = 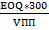30000*300/450000
Уровень запаса, при котором необходимо сделать очередной заказ, м Ур.З = VПП / 300 *t 450000/300*5
Минимальная сумма затрат по завозу и хранению, руб. Lmin = Ц 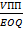рз * + С хрз * 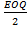100000*450000/30000 + 100*30000/2
Оптимальный средний размер заказа при годовой потребности в 600000 м EOQ =

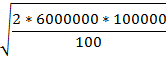
Продолжение таблицы 7.4

Общая сумма затрат при условии заказа в размере 20000м, руб. Lmin = Ц 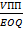рз * + С хрз * 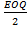100000*450000/20000 + 100*20000/2
Общая сумма затрат при условии заказа в размере 40000м, руб. Lmin = Ц 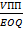рз * + С хрз * 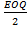100000*450000/40000 + 100*40000/2
Затраты по завозу и хранению при резервном запасе в 3000 м, руб. Lmin = Ц 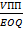рз * + С хрз * 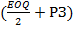100000*450000/30000+100*(30000/2+3000)

Дата добавления: 2017-02-01