Необходимые теоретические сведения 2 страница

Теорема 3.9 (о башне расширений полей). Если поле есть расширение поля 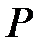степени 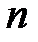, а поле 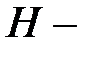расширение 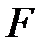степени 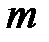, то 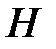есть расширение 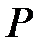степени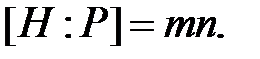

Следствие. Если степень расширения 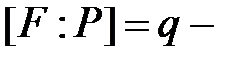число простое, то поле 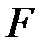не содержит подполей, промежуточных между 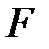и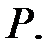

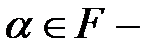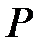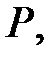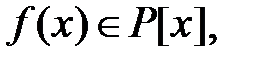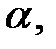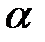Определение 3.10. Элемент расширения поля является алгебраическим над полем если существует полином корнем которого является то есть В противном случае называют трансцендентным над 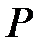элементом. Поле 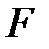называется алгебраическим расширением поля 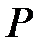, если всякий элемент из является алгебраическим над полем .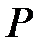

Теорема 3.10. Всякое конечное расширение произвольного поля Р является алгебраическим над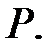

Теорема 3.11. Пусть алгебраический над полем 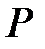элемент. Множество 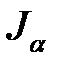полиномов для которых 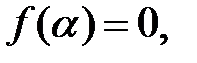есть максимальный идеал кольца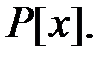

Следствие. Пусть 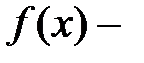неприводимый полином из 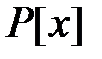с корнем 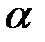из расширени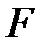я поля 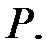Пусть для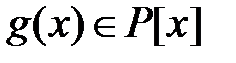 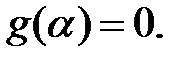Тогда 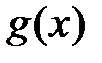делится на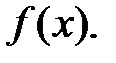

Определение 3.11. Пусть 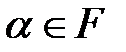– алгебраический над полем 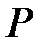элемент. Минимальным полиномом элемента 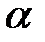над полем 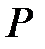называется неприводимый полином в кольце 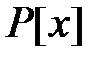, старший коэффициент которого равен 1, а одним из корней является элемент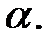

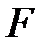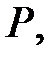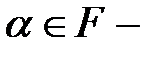Теорема 3.12. Пусть – расширение поля пусть алгебраический над 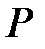элемент с минимальным над 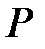полиномом степени 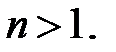Пусть 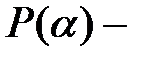минимальное подполе поля 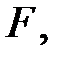содержащее 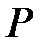и 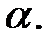Тогда степень расширения 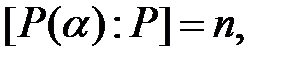а поле 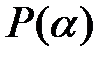имеет следующую структуру: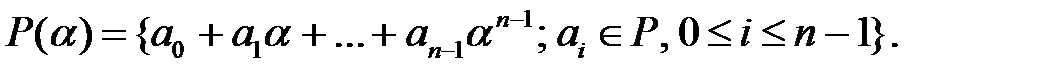

Теорема 3.13. В условиях теоремы 3.11 поле 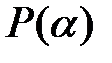изоморфно фактор-кольцу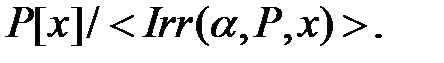

Конечные поля были впервые введены в математическую практику в начале XIX в. гениальным французским математиком Эваристом Галуа. Поэтому конечные поля часто называют полями Галуа, а на письме обозначают через 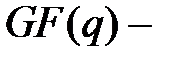поле Галуа из 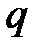элементов. Будем использовать и более краткое обозначение этого же поля 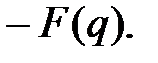Из вышесказанного мы уже знаем некоторые основные свойства конечных полей.

Теорема 3.14. Любое конечное поле 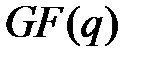имеет конечную характеристику 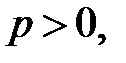является конечным расширением поля 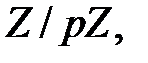содержит 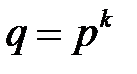элементов, при этом 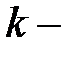степень расширения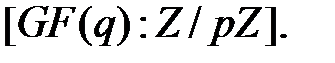

Из теоремы Лагранжа о конечных группах следует, что все элементы мультипликативной группы 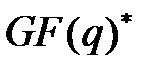удовлетворяют уравнению 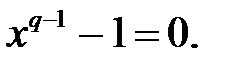На самом деле имеет место теорема 3.5.

Теорема 3.15. (о существовании и единственности конечного поля). Для каждого простого числа 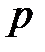и для любого натурального существует конечное поле из 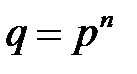элементов. Это поле единственно с точностью до изоморфизма, состоит из корней уравнения 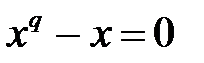и только из них.

Взаимоотношения между подполями поля Галуа выражает теорема 3.16.

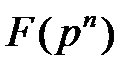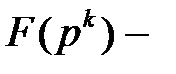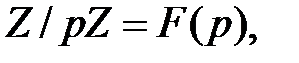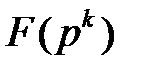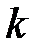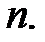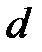
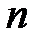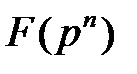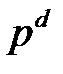Теорема 3.16. Пусть и конечные поля, расширения поля причем Поле является подполем тогда и только тогда, когда делит Для каждого натурального делителя числа существует и единственно подполе из элементов.

Ненулевые элементы поля 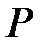образуют группу относительно умножения. Ее называют мультипликативной группой поля и обозначают 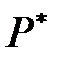. Теорема 3.15 характеризует ненулевые элементы полей Галуа как корни из 1. Мультипликативные свойства корней из 1 и в полях характеристики 0 и любой характеристики 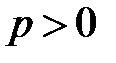идентичны.

Теорема 3.17. Мультипликативная группа конечного поля – циклическая.

Определение 3.12. Образующие мультипликативной группы конечного поля называют примитивными элементами этого поля.

Известно, что каждый примитивный элемент поля Галуа 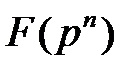является корнем неприводимого полинома степени 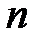из кольца 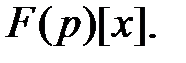Если 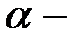примитивный элемент поля 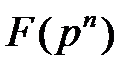, корень неприводимого полинома 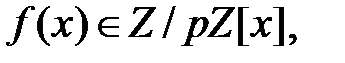то и остальные корни этого полинома являются примитивными элементами поля .

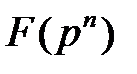Теорема 3.18. Пусть 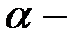корень неприводимого полинома 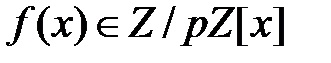степени 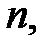принадлежащий полю 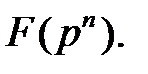Тогда остальными корнями полинома 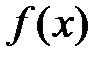являются элементы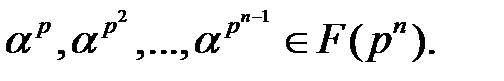

Определение 3.13. Неприводимый полином 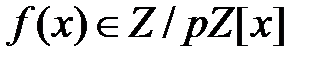степени 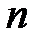называется примитивным полиномом, если его корни – примитивные элементы поля Галуа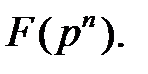

Известно, что для каждого натурального 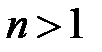в кольце 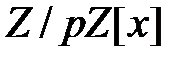существуют примитивные полиномы степени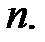

Характеризация конечных полей как множеств корней уравнений специального вида позволила доказать единственность таких полей данного порядка. Для организации вычислений в конечных полях требуется явное конструктивное задание полей Галуа, четкая методика формирования элементов этих полей. Данной цели служит теорема 3.19.

Теорема 3.19. Для каждого натурального и фиксированного простого числа 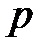существует единственное расширение 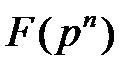поля 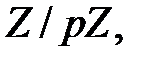состоящее из 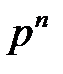элементов, оно изоморфно полю 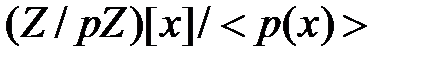для любого неприводимого полинома 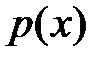степени 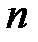из кольца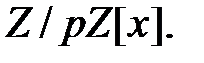

Следствие. Всякое конечное поле 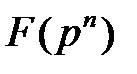состоит из всевозможных полиномов степени, меньшей 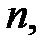с коэффициентами из поля 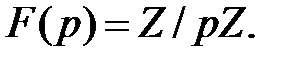Складываются и вычитаются эти полиномы как обычно, умножаются почленно с учетом равенства для фиксированного неприводимого полинома степени 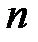из кольца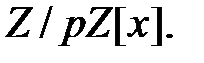

Заметим, что полиномиальное задание элементов поля 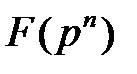легко преобразуется в векторное: полиному 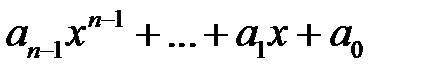однозначно соответствует вектор .

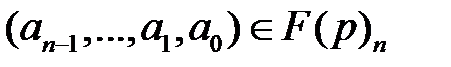Пример 3.5. Сформируем поле 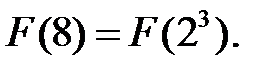Поскольку 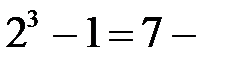число простое, то над полем из двух элементов все неприводимые полиномы третьей степени являются примитивными. Зафиксируем неприводимый полином степени 3, например 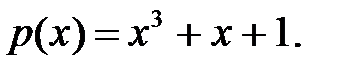Обозначим через a его корень, принадлежащий 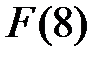. Тогда 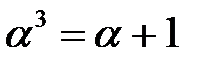(так как характеристика поля 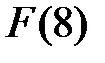равна 2, то –1=1). Тогда a⁴=a²+a, a⁵=a³+a²=a²+a+1, a⁶=a³+a²+a=a²+1, a⁷=a³+a=a+a+1=1, 0=a^-¥. Следовательно, поле можно задать в виде таблицы из трех столбцов, в левом столбце запишем все различные степени a, в среднем – соответствующие этим степеням суммы вида 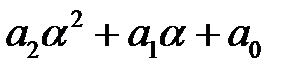, в правом – трехмерные векторы с координатами из поля .

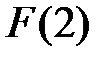Таблица элементов поля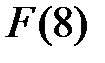

a^-¥ | 0 (000)

a¹ | a (010)

a² | a² (100)

a³ | a+1 (011)

a⁴ | 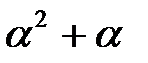(110)

a⁵ | a²+a+1 (111)

a⁶ | a²+1 (101)

a⁷ | 1. (001)

Векторное задание полей Галуа служит для альтернативного задания кодов Хемминга – в качестве проверочной матрицы кода берется матрица 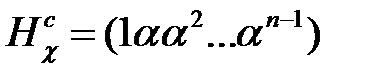для 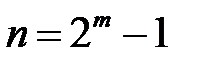и примитивного элемента поля 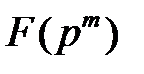. Фактически, такая запись матрицы есть последовательное задание элементов циклической группы .

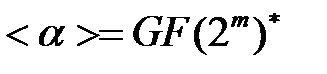Определение 3.14. Линейный код называется циклическим, если для каждого кодового вектора-слова 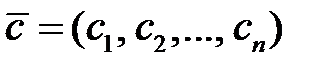кодовым словом будет и вектор 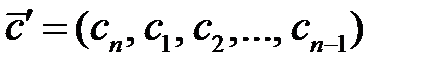, получаемый из вектора 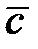циклическим сдвигом его координат.

Известно, что код с проверочной матрицей 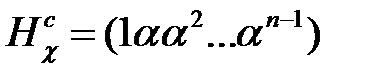является циклическим. Данная матрица отличается от лексикографического задания кода лишь перестановкой столбцов.

Определение 3.15. Линейные коды, отличающиеся перестановкой отсчетов (столбцов проверочных матриц), называются эквивалентными.

Пример 3.6. На основании приведенного задания поля 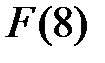построим проверочную матрицу кода Хемминга длиной 7.

.

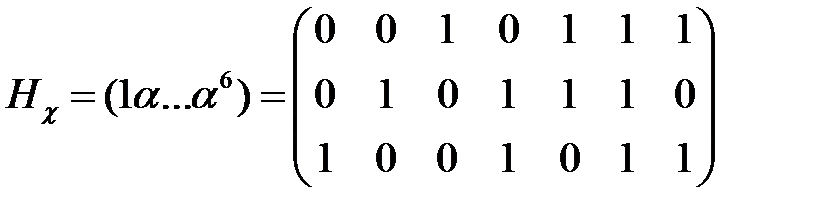Дата добавления: 2017-02-01