Необходимые теоретические сведения

Циклическое задание кодов Хемминга с помощью проверочной матрицы обеспечило возможности различных преобразований этих матриц. Подобные эксперименты быстро привели к новым кодам с большим минимальным расстоянием и широким декодирующим потенциалом. Первыми и наиболее удачными из них оказались примитивные коды Боуза-Чоудхури-Хоквингема (БЧХ-коды) с минимальным расстоянием 5. Эти коды имеют длину , размерность , где степень поля поля определения кода Хемминга такой же длины, поля определения и данного БЧХ-кода. Будем данные коды обозначать через . Проверочная матрица данного кода имеет вид:

. (4.1)

Данный код корректирует одиночные и двойные ошибки. Синдром одиночной ошибки совпадает с одним из столбцов проверочной матрицы, который четко указывает на ошибочное место в принятом векторе-сообщении. Для определения координат двойной ошибки следует решать подходящее квадратное уравнение. Напомним некоторые факты о них.

Прежде всего отметим, что стандартные формулы корней квадратного уравнения в полях характеристики 2 не применимы, так как деление на 2 здесь равносильно делению на 0. Однако всякое квадратное уравнение с коэффициентами приводится к каноническому виду, то есть к виду 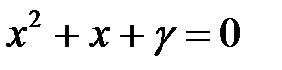для некоторого 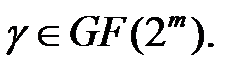Если один из корней уравнения то другим корнем этого уравнения является

Теорема 4.1 (Берлекемп, Рамсей, Соломон, 1967). Уравнение с элементом имеет корни в этом же поле тогда и только тогда, когда след

Напомним, что след в полях Галуа 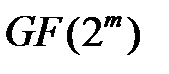вычисляется по формуле При этом правильно вычисленный след принимает только одно из двух значений: 0 или 1.

Формула корней квадратного уравнения в полях Галуа характеристики 2 выводится с помощью нормального базиса в векторном пространстве над полем . Напомним, что нормальный базис имеет вид: для некоторого . Дэвенпорт в 1968 г. доказал, что всякое конечное расширение поля Галуа обладает нормальным базисом. Несложное рассуждение показывает, что элемент 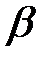из нормального базиса должен быть примитивным элементом поля и иметь след, равный 1. Поэтому для произвольного , заданного в нормальном базисе равенством где , след Формула квадратных корней выглядит достаточно экзотично.

Теорема 4.2. (Чэнь, 1982). Пусть у квадратного уравнения с элементом след Пусть нормальный базис поля 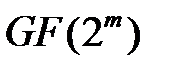над полем Пусть разложение по нормальному базису для Тогда является корнем уравнения

Пример 4.1. Решим квадратное уравнение над полем с примитивным элементом корнем полинома по формулам Чэня из теоремы 4.2. Для этого приведём уравнение к каноническому виду с помощью замены . Получим уравнение с . При этом след .

Выясним, образуют ли нормальный базис в поле степени примитивного элемента . Ранг данной системы векторов над полем равен рангу матрицы из координат этих векторов в базисе . В этой матрице две одинаковые строки – вторая и пятая, поэтому перечисленные элементы базиса не образуют. Аналогичная проверка показывает, что нормальным базисом здесь является система

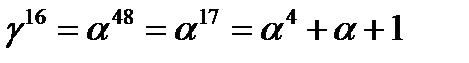. Действительно, матрица из координат этих векторов перестановкой строк преобразуется к треугольному виду и, следовательно, имеет ранг 5. Непосредственные вычисления позволяют найти обратную матрицу: .

Как известно из линейной алгебры, координаты вектора в найденном нормальном базисе вычисляются с помощью матрицы

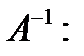
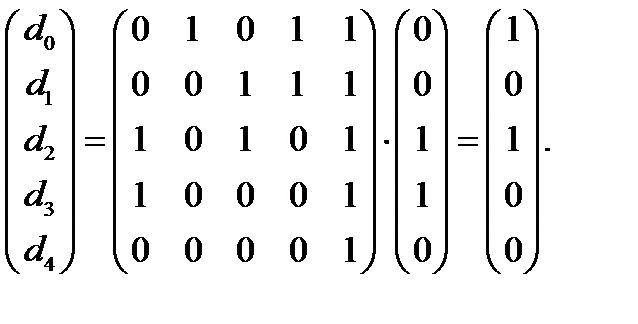
Найдём корни полученного уравнения по формулам из теоремы 4.2: . Следовательно, первый корень , а второй корень . Тогда корни исходного уравнения

Как видим, применение формул Чэня для решения квадратных уравнений требует достаточно много промежуточных громоздких вычислений. Сам автор этих формул предложил решать квадратные уравнения простым перебором – последовательной подстановкой элементов поля в уравнение до получения нуля. Метод этот называют в литературе методом Чэня.

Вернемся к двойным ошибкам в БЧХ-коде . Пусть при передаче вектора-сообщения в цифровой системе связи с данным кодом на сообщение наложился вектор-ошибка 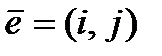весом 2 с ненулевыми координатами на неизвестных позициях 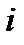и . Это означает, что приёмное устройство связи приняло сообщение . В соответствии со свойствами и структурой матрицы синдром , где . Величины и являются неизвестными элементами поля Галуа . Обозначим их через и соответственно. Эти величины – решения системы уравнений

(4.2)

Преобразуем второе уравнение системы (4.2):

.

Следовательно, . Правую часть полученного равенства обозначим через . Таким образом, система преобразована к виду:

Согласно теореме Виета, корни системы являются корнями квадратного уравнения Решив уравнение, найдём 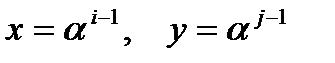, а с ними и вектор-ошибку .

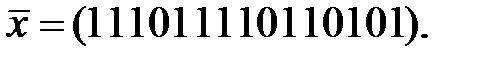Пример 4.2. В системе связи, построенной на основе БЧХ-кода с проверочной матрицей примитивный элемент поля Галуа корень полинома принято сообщение Выяснить наличие ошибок в этом сообщении и попытаться их исправить.

Решение. Для проведения вычислений необходимо иметь под рукой сформированное поле Галуа из 16 элементов, а именно таблицу степеней 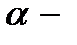корня полинома 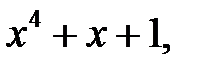и их полиномиальных эквивалентов. Все кодовые слова 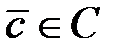(и только они) составляют ядро проверочной матрицы: 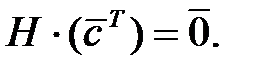Если то сообщение 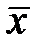явно содержит ошибки. В данном случа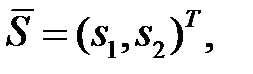е где

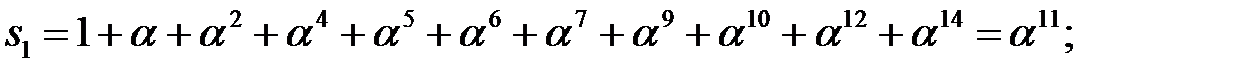
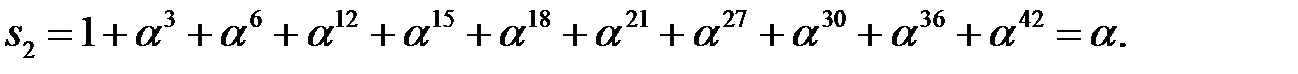
Таким образом, полученное сообщение 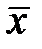содержит ошибки. Данный код исправляет двойные ошибки. Для нахождения такой ошибки имеем следующую конкретную систему :

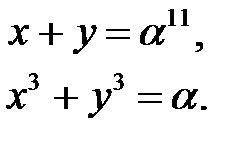
Данная система сводится к квадратному уравнению. Действительно, 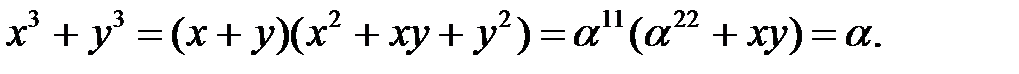Отсюда получаем Замена приводит это уравнение к следующему квадратному уравнению: 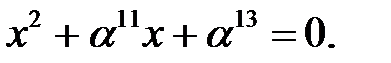После замены 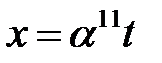данное квадратное уравнение приводим к каноническому виду 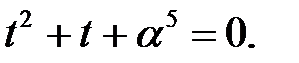Нетрудно проверить, что след 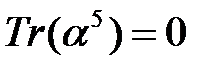и, следовательно, уравнение имеет решения в поле 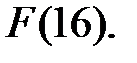Непосредственным подбором (методом Чэня) можно убедиться, что корнями являются 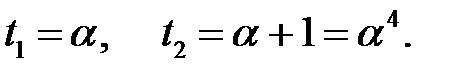Тогда Таким образом, ошибочными в принятом сообщении являются 1-я и 13-я позиции и правильным является сообщение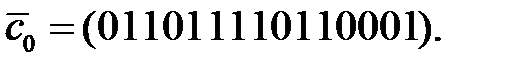

К семейству БЧХ-кодов примыкают и реверсивные коды . Они (те же параметры и , что и БЧХ-коды ) задаются проверочной матрицей , где , , примитивный элемент поля Галуа . Реверсивные коды имеют при четных и при нечетных значениях .

Декодирование двойных ошибок реверсивным кодом аналогично той же процедуре в БЧХ-кодах. Только вместо системы (4.2) здесь появляется система

(4.3)

Второе уравнение системы (4.3) легко преобразуется к виду . Дальнейший переход к квадратному уравнению очевиден.

Дата добавления: 2017-02-01