Синдромное декодированиепроизвольных БЧХ-кодов

Задания для самостоятельной работы

Задания для аудиторной работы

Задание 1. Сформировать матрицу 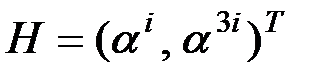БЧХ-кода длиной 7, где 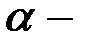корень полинома 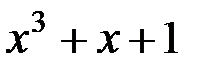. Найти порождающую матрицу этого кода.

Решение. Проверочная матрица кода имеет вид:

.

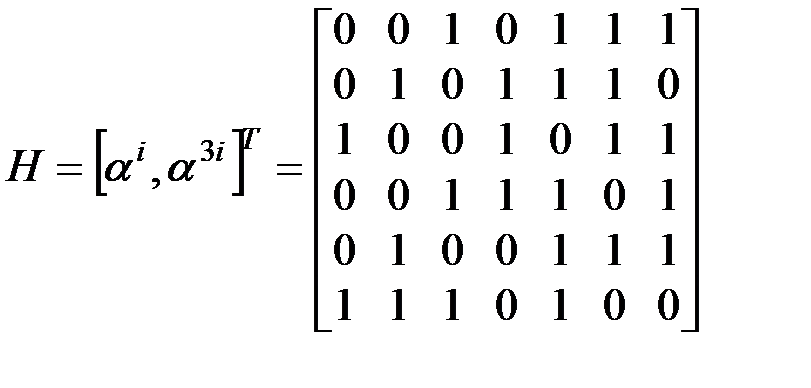Для нахождения порождающей матрицы кода следует вспомнить решение первого задания в ПЗ№2.

Задание 2. ТКС функционирует на основе БЧХ-кода из задания 1. Его приёмное устройство приняло сообщение 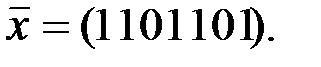Содержатся ли ошибки в данном сообщении?

Решение. Синдром ошибок принятого сообщения 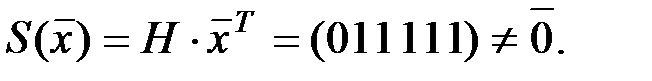Следовательно, принятое сообщение содержит ошибки.

Задание 3. Найти вектор ошибок в принятом сообщении (задание 2) и указать правильное сообщение.

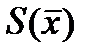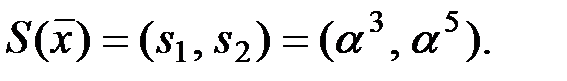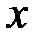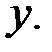Решение. В силу структуры проверочной матрицы данного кода синдром состоит из двух компонент: Синдром не совпадает ни с одним из столбцов матрицы Поэтому сообщение содержит ошибку кратности, большей 1. Предположим, что в процессе передачи произошла двойная ошибка с неизвестными локаторами и Тогда 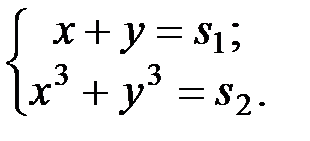В данном случае эта система имеет вид: 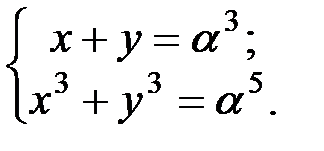Сведём систему к квадратному уравнению. 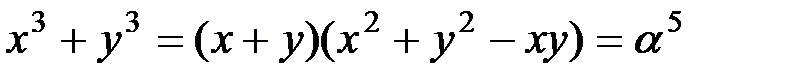. 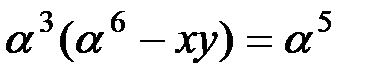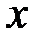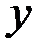С учётом первого уравнения имеем или Согласно теореме Виета, и являются корнями квадратного уравнения 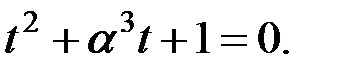Приведём уравнение к каноническому виду заменой 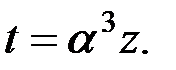Получим уравнение 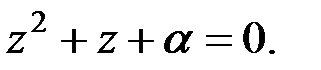Критерий разрешимости квадратных уравнений в каноническом виде гласит, что такое уравнение имеет решения тогда и только тогда, когда 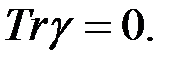В данном случае 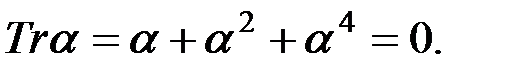Таким образом, уравнение 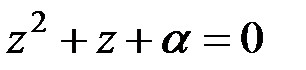имеет корни в поле Галуа 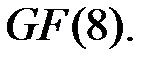Найдём эти корни по формулам Чэня. Чтобы ими воспользоваться, необходимо найти нормальный базис поля 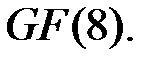В данном случае нормальный базис имеет вид 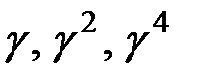для некоторого элемента поля 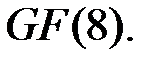При этом след 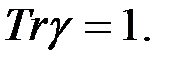Попробуем взять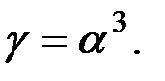 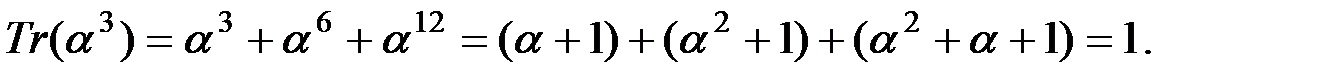Элементы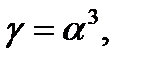 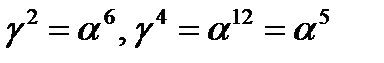линейно независимы над 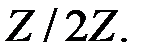Ведь матрица из координат этих элементов как векторов трёхмерного пространства над полем 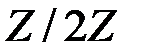имеет определитель 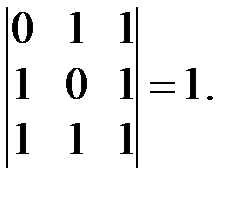Найдём разложение 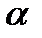по нормальному базису, то есть такие 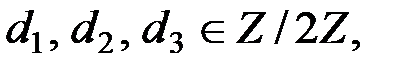что 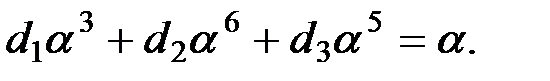Это равенство в координатной форме приводит к следующей СЛАУ: 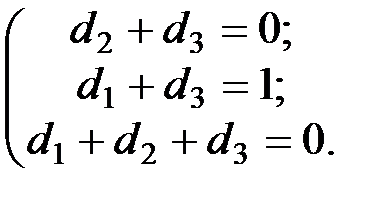Легко видеть, что система имеет единственное решение: 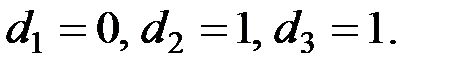Согласно формулам Чэня, уравнение 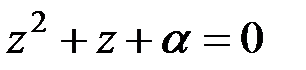имеет корни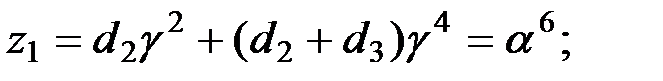 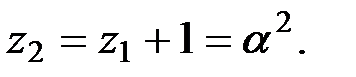Тогда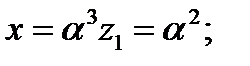

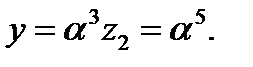
Найденные локаторы однозначно указывают, что в принятом сообщении произошла двойная ошибка на третьей и шестой позициях и правильное сообщение имеет вид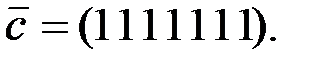

Задание 4. Сформировать матрицу кода БЧХ длиной 15, где 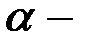корень полинома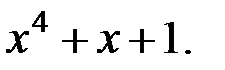

Задание 5. ТКС функционирует на основе БЧХ-кода из задания 4. Его приёмное устройство приняло сообщение 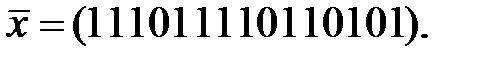Выяснить наличие ошибок в этом сообщении.

Решение. Для проведения вычислений необходимо иметь под рукой сформированное поле Галуа из 16 элементов, а именно таблицу степеней 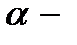корня полинома 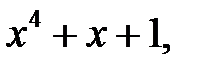и их полиномиальных эквивалентов. Все кодовые слова 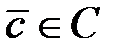(и только они) составляют ядро проверочной матрицы: 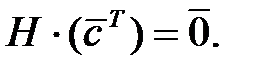Если то сообщение 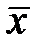явно содержит ошибки. В данном случа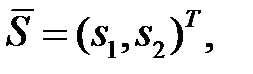е где

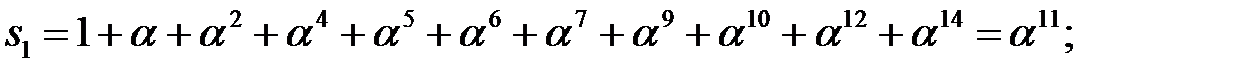
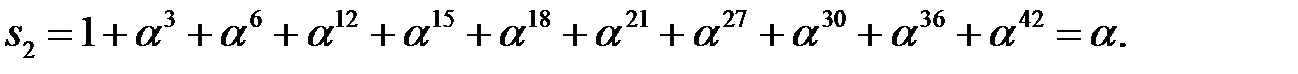
Таким образом, полученное сообщение 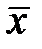содержит ошибки.

Задание 6. Найти вектор ошибок в принятом сообщении (задание 2) и указать правильное сообщение.

Данный код исправляет двойные ошибки. Для нахождения такой ошибки имеем следующую конкретную систему

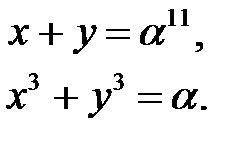(4.4)

Система (4.4) сводится к квадратному уравнению. Действительно, 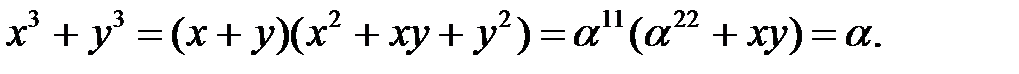Отсюда получаем Замена приводит это уравнение к следующему квадратному уравнению: 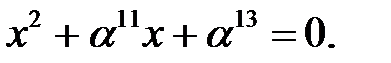После замены 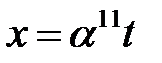данное квадратное уравнение приводим к каноническому виду 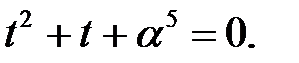Нетрудно проверить, что след 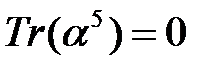и, следовательно, уравнение имеет решения в поле 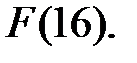Непосредственным подбором (методом Чэня) можно убедиться, что корнями являются 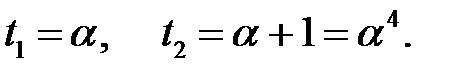Тогда Таким образом, ошибочными в принятом сообщении являются 1-я и 13-я позиции и правильным является сообщение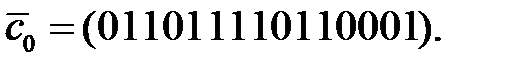

Задание 1. Проверить на неприводимость и примитивность заданный полином над полем 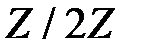(по вариантам).

Задание 2. Сформировать с помощью полинома из задания 1 поле Галуа из 32-х элементов.

Задание 3. Сформировать проверочную матрицу (31, 21)-БЧХ-кода (варианты 1–6, 13 –15) или реверсивного кода (варианты 7 – 12) на основании поля Галуа из задания 2.

Задание 4. Выяснить наличие ошибок в принятом сообщении (по вариантам) в ТКС с БЧХ-кодом из задания 3.

Задание 5. Методом квадратных уравнений исправить ошибки в принятом сообщении из задания 4.

Вариант 1: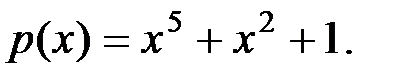

Вариант 2: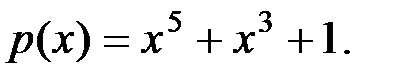

Вариант 3: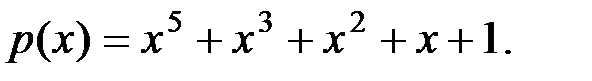

Вариант 4: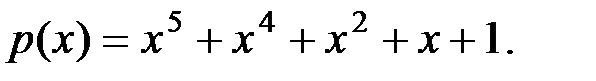

Вариант 5:

Вариант 6: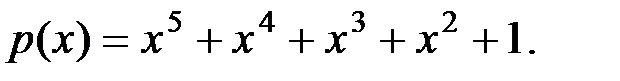

Вариант 7:

Вариант 8: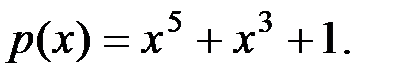

Вариант 9:

Вариант 10: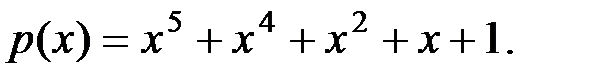

Вариант 11:

Вариант 12: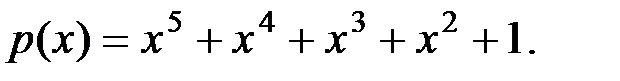

Вариант 13: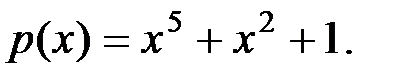

Вариант 14: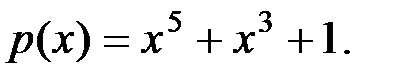

Вариант 15: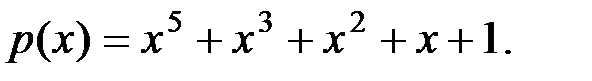

Задание 6.

Вариант 1: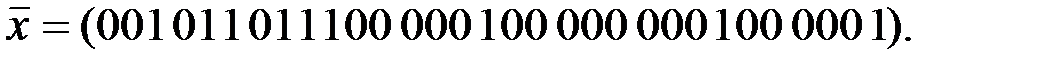

Вариант 2: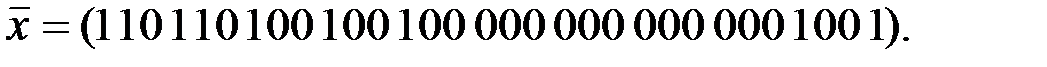

Вариант 3: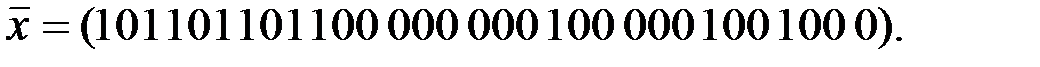

Вариант 4: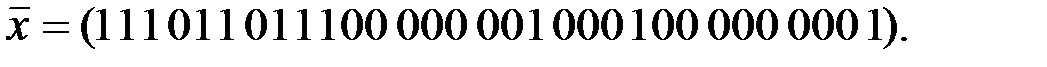

Вариант 5: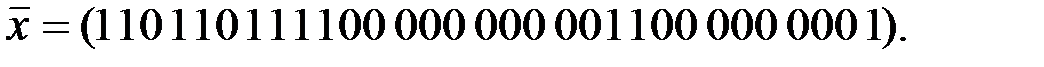

Вариант 6: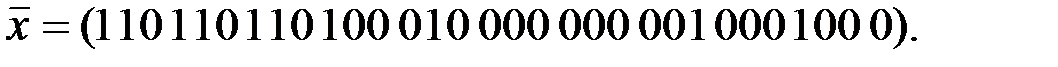

Вариант 7: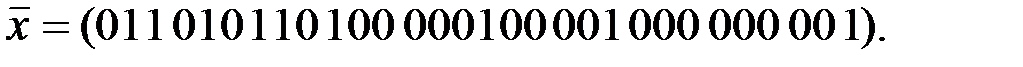

Вариант 8: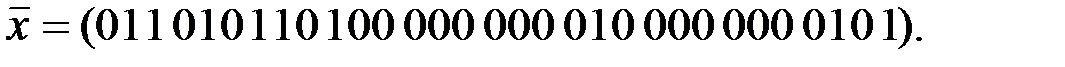

Вариант 9:

Вариант 10: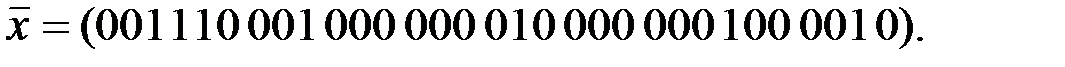

Вариант 11: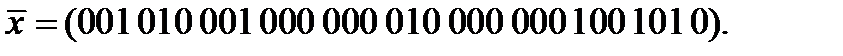

Вариант 12: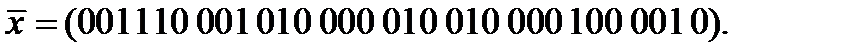

Вариант 13: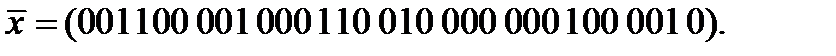

Вариант 14: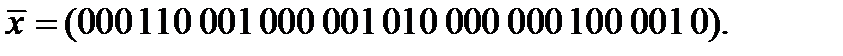

Вариант 15:

Практическое занятие №5

Дата добавления: 2017-02-01