Необходимые теоретические сведения 1 страница

Задания для самостоятельной работы

Задания для аудиторной работы

Задание 1. В (15,3)-БЧХ-коде с проверочной матрицей где корень полинома , принято сообщение 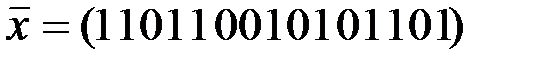с синдромом ошибок . Найти вектор ошибок в этом сообщении, если известно, что произошла ошибка весом 3.

Решение. Тройная ошибка в сообщении произошла на неизвестных позициях В подматрице матрицы позициям соответствуют столбцы Эти столбцы образно называют локаторами ошибочных позиций. Их рассматриваем как элементы поля Галуа , задаваемые с помощью полинома . Синдром получается двоичным сложением столбцов матрицы с номерами . Каждый й столбец матрицы состоит из трёх частей, интерпретируемых как элементы поля . Поэтому для определения истинных значений позиций искомой тройной ошибки мы с помощью синдрома получаем следующую систему уравнений:

Левые части уравнений системы есть симметрические степенные полиномы от трёх переменных . Здесь У нас, в условиях двоичной арифметики, 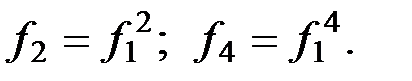В теория симметрических полиномов существуют формулы, принадлежащие перу великого Ньютона, и которые связывают степенные симметрические полиномы с элементарными симметрическими полиномами . Элементарные симметрические полиномы от трёх переменных 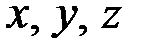выглядят следующим образом: .

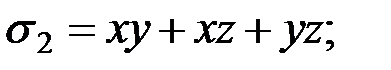
В полях характеристики 2 формулы Ньютона, связывающие с , имеют специальный вид:

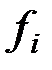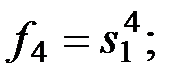
Подставим в систему значения из системы : Получим следующую систему линейных уравнений относительно неизвестных :

Подставим в значения . Получим систему

Отсюда следует

Следовательно, или Таким образом, Полученные значения служат, согласно теореме Виета, коэффициентами кубического уравнения , корнями которого и являются искомые в системе неизвестные . Итак, решение системы сводится к поиску корней кубического уравнения в поле .

Метод Чэня, то есть последовательная подстановка в уравнение элементов поля вместо , позволяет найти следующие его корни: Корни однозначно указывают тройную ошибку на 1-й, 10-й и 14-й позициях в сообщении Следовательно, отправлено было истинное сообщение

Задание 1. Пусть ТКС функционирует на основе БЧХ-кода длиной 31 с проверочной матрицей 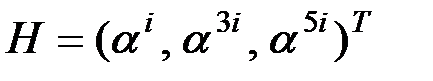для примитивного элемента поля 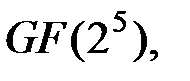корня полинома 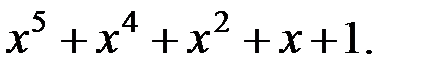Пусть приёмное устройство ТКС приняло сообщение с синдромом ошибок Найти ошибку в данном сообщении.

Решение. Кубическое уравнение получается преобразованием системы уравнений

Требуемое кубическое уравнение имеет вид 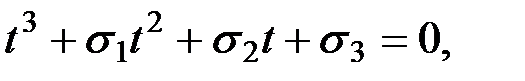где находятся из СЛАУ: В данном случае СЛАУ имеет вид: Вычисления показывают, что Таким образом, получаем следующее кубическое уравнение: Применяя достаточно монотонный метод Чэня, находим корни этого уравнения: Вычисленные локаторы однозначно определяют вектор-ошибку

Задание 1. В БЧХ-коде с проверочной матрицей где корень примитивного полинома принято сообщение с синдромом Найти вектор ошибок в принятом сообщении сведением задачи к кубическому уравнению и решением этого уравнения методом Чэня.

Вариант 1:

Вариант 2:

Вариант 3:

Вариант 4:

Вариант 5:

Вариант 6:

Вариант 7

Вариант 8

Вариант 9:

Вариант 10:

Вариант 11:

Вариант 12:

Вариант 13:

Вариант 14:

Вариант 15:

Практическое занятие №6

Циклическая и циклотомическая классификация векторов-ошибок

На первом курсе мы хорошо изучили конечномерные векторные пространства и их линейные операторы на этих пространствах. Установили, что всевозможные линейные преобразования пространства составляют матричное кольцо Автоморфизмами пространства являются невырожденные квадратные матрицы из они образуют группу Поэтому естественно было бы считать группой автоморфизмов кода группу Однако по традиции, сложившейся на заре возникновения теории и практики помехоустойчивого кодирования, автоморфизмы линейных имеют более узкие рамки.

Определение 6.1. Автоморфизмом кода называется произвольная перестановка координат кодовых слов, которая преобразует кодовые слова в новые кодовые слова.

Теорема 6.1. Множество линейного кода длиной есть подгруппа группы подстановок

Пусть оператор циклического сдвига координат векторов, действие которого на произвольный вектор пространства осуществляется по следующему простому правилу: 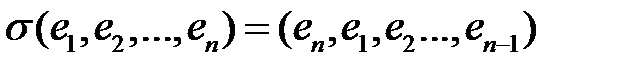. Оператор является одним из наиболее естественных примеров нетривиальных автоморфизмов линейных кодов. Об этом свидетельствует теорема 6.2

Теорема 6.2. Оператор является автоморфизмом кодов Хемминга с проверочной матрицей , БЧХ-кодов с проверочной матрицей (4.1), реверсивных кодов из ПЗ4.

Следствие. У каждого кода длиной из теоремы 5.2 группа автоморфизмов содержит циклическую подгруппу порядка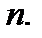

Определим на множестве преобразование по следующему правилу: для каждого элемент множества равный если и равный если

Лемма 6.1. Отображение является биекцией множества тогда и только тогда, когда нечетно.

Предложение 6.1. Пусть наименьшее натуральное число с условием: делится на данное нечётное число Циклическая группа 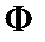, порожденная степенями подстановки на множестве , конечна и имеет порядок .

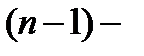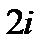Группа Ф действует на пространстве ошибок любого двоичного линейного кода, переставляя координаты векторов-ошибок в соответствии с действием на их номера, образующие множество Вообще говоря, здесь уместно было бы нумеровать координаты не с 1-й по ю, а с 0-й по ую. 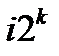Тогда правила действия и ее степеней на ю координату, выглядят проще: где – вычет целого числа по модулю Соответственно, остаток от деления на При этом заметим, что числа образуют циклотомический класс по модулю [3]. Поэтому подстановки – называются циклотомическими и, соответственно, группа Ф – циклотомической.

Теорема 6.3. Циклотомическая группа 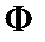является подгруппой группы кодов Хемминга, БЧХ-кодов с проверочной матрицей (4.1), реверсивных кодов – кодов, перечисленных в теореме 5.2.

Лемма 6.2. Для произвольного .

Теорема 6.4. Группа подстановок порождённая циклической подстановкой и циклотомической подстановкой некоммутативна и имеет порядок

Определение 6.2. Равенство означает, что двоичный вектор имеет ненулевыми и, следовательно, равными 1 только координаты под номерами

Важнейшим для дальнейшего является определение 6.3

Определение 6.3. Совокупность всех попарно различных векторов-ошибок называется Г-орбитой вектора-ошибки ē в пространстве ошибок и обозначается через Г-орбита называется полной, если она содержит различных векторов, в противном случае Г-орбиту называют неполной.

Г-орбиты имеют четкую структуру, которую описывает теорема 6.5

Теорема 6.5. Для произвольного фиксированного вектора из пространства ошибок его Г-орбита состоит из λ элементов, где 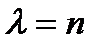или 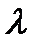делит При этом наименьшее натуральное число с условием 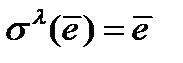и Г-орбита имеет следующую структуру:

. (6.1)

Для любых двух векторов-ошибок и из их Г-орбиты и < > либо совпадают, либо не имеют одинаковых элементов.

Структурная формула (6.1) произвольной Г-орбиты показывает, что действие Г на элементы из не выводит за пределы Г-орбиты и что Г действует транзитивно внутри , то есть для всяких векторов ē_i, ē_{j ,} из найдется g ÎГ, при котором . Этот факт дополняет предложение 6.2

Предложение 6.2. Для любых двух векторов-ошибок и из Е_n их Г-орбиты и < > либо совпадают, либо не имеют одинаковых элементов.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

Рис.6.1. Схематическое изображение вектора =(1,2,6,7,11,12) из пространства и его циклических сдвигов  

Из теоремы 6.5 и предложения 6.2 следует, что под действием группы Г циклических сдвигов пространство разбивается на непересекающиеся классы – Г-орбиты. Всякое разбиение множества на непересекающиеся классы определяет отношение эквивалентности на нём. Множество всех Г-орбит пространства будем обозначать через

Пример 6.1. Построим классификацию, то есть систему Г-орбит в двоичном 4-мерном пространстве векторов-ошибок Е ₄. Здесь = 6; 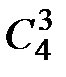= 4; и

Пусть = (1000). Тогда < > = {(1000),(0100),(0010),(0001)}.

Пусть = (1100). Тогда < > = {(1100),(0110),(0011),(1001)}.

Пусть = (1010). Тогда < > = {(1010),(0101)}.

Пусть = (1110). Тогда < > = {(1110),(0111),(1011),(1101)}.

Очевидно, Г-орбиты, порождённые векторами = (0000) и = (1111), имеют мощность, равную 1.

Таким образом, пространство Е _4, состоящее из 16 векторов-ошибок, разбивается на 6 Г-орбит: две – < > и < > – мощности 1, одну – <(1010)> – мощности 2 и три – <(1000)>, <(1100)>, <(1110)> – мощности 4. Таким образом, множество состоит из 6 элементов.

Дата добавления: 2017-02-01