
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Необходимые теоретические сведения 2 страница
|
|
|
|
Определение 6.4. (Циклическим) пакетом ошибок длиной  называется вектор
называется вектор  , все ненулевые координаты которого расположены среди
, все ненулевые координаты которого расположены среди  последовательных (по циклу) координат, первая и последняя из которых отличны от нуля. Пакет ошибок называется сплошным, если вес ошибки совпадает с длиной пакета.
последовательных (по циклу) координат, первая и последняя из которых отличны от нуля. Пакет ошибок называется сплошным, если вес ошибки совпадает с длиной пакета.
На рис. 6.2. приведены все возможные пакеты ошибок длиной 3 в пространстве  , где
, где  поле Галуа из двух элементов 1 и 0.
поле Галуа из двух элементов 1 и 0.
а)
б)
Рис.6.2.Пакеты векторов-ошибок длиной 3 в пространстве  над полем
над полем 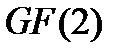 : а) весом 3; б) весом 2
: а) весом 3; б) весом 2
Определение 6.5. Всякую вектор-ошибку ē весом  можно интерпретировать различным образом как пакетную ошибку с соответствующими значениями длины b. Наименьшую из длин b при всех таких интерпретациях вектора-ошибки ē назовем диаметром D этого вектора-ошибки.
можно интерпретировать различным образом как пакетную ошибку с соответствующими значениями длины b. Наименьшую из длин b при всех таких интерпретациях вектора-ошибки ē назовем диаметром D этого вектора-ошибки.
Пример 6.2. Вектор-ошибка ē = (100010) – есть ошибка веса  в кодовом слове длиной n = 6, его можно рассматривать как пакет ошибок длиной 5 или пакет длиной 3. Таким образом, диаметр D этого вектора-ошибки равен 3.
в кодовом слове длиной n = 6, его можно рассматривать как пакет ошибок длиной 5 или пакет длиной 3. Таким образом, диаметр D этого вектора-ошибки равен 3.
Предложение 6.3. Диаметр вектора-ошибки ē весoм ω >1 с ненулевыми координатами на позициях i1, i2…iω вычисляется по формуле
 (6.2)
(6.2)
В частности, при 
 (6.3)
(6.3)
при 
 (6.4)
(6.4)
Следствие 1. Диаметры векторов-ошибок весом 2 в точности принадлежат отрезку [2; [ n /2]+1].
Предложение 6.4. Пусть  двоичное векторное пространство. Одиночные ошибки составляют один класс эквивалентности I 1. Векторы-ошибки веса 2 принадлежат одному классу эквивалентности (Г-орбите) тогда и только тогда, когда их диаметры совпадают. По значениям диаметра множество всех двойных ошибок разбивается на ν непересекающихся классов эквивалентности I 2, I3,…, Iν+1, где ν =
двоичное векторное пространство. Одиночные ошибки составляют один класс эквивалентности I 1. Векторы-ошибки веса 2 принадлежат одному классу эквивалентности (Г-орбите) тогда и только тогда, когда их диаметры совпадают. По значениям диаметра множество всех двойных ошибок разбивается на ν непересекающихся классов эквивалентности I 2, I3,…, Iν+1, где ν =  – целая часть числа
– целая часть числа  , Ik – класс двойных ошибок диаметра k, 2≤ k ≤ν+1. Для нечетных
, Ik – класс двойных ошибок диаметра k, 2≤ k ≤ν+1. Для нечетных  каждый из классов Ik состоит из
каждый из классов Ik состоит из  различных ошибок. При четных
различных ошибок. При четных  класс
класс  где
где 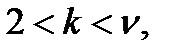 состоит из
состоит из  векторов-ошибок, а класс Iν+1 – из
векторов-ошибок, а класс Iν+1 – из  двойных ошибок.
двойных ошибок.
Пример 6.3. В пространстве  имеется
имеется  векторов-ошибок веса 2, делящихся, согласно предложению 3.7, на 7 полных Г-орбит в соответствии со значением их диаметров. Ниже приведена табл. 6.1 образующих Г-орбит двойных ошибок в 15-мерном пространстве – векторов-ошибок
векторов-ошибок веса 2, делящихся, согласно предложению 3.7, на 7 полных Г-орбит в соответствии со значением их диаметров. Ниже приведена табл. 6.1 образующих Г-орбит двойных ошибок в 15-мерном пространстве – векторов-ошибок  диаметра
диаметра  .
.
| Таблица 6.1 | |||||||||||||||||
Г-орбиты двойных ошибок в пространстве 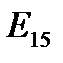
| |||||||||||||||||

| 
| Координаты порождающего вектора 
| |||||||||||||||

| |||||||||||||||||

| |||||||||||||||||

| |||||||||||||||||

| |||||||||||||||||

| |||||||||||||||||

| |||||||||||||||||

| |||||||||||||||||
Определение 6.6. Совокупность всех различных векторов  для данного фиксированного вектора
для данного фиксированного вектора  называется Ф-орбитой или циклотомической орбитой вектора
называется Ф-орбитой или циклотомической орбитой вектора  при действии группы Ф на пространстве
при действии группы Ф на пространстве  и обозначается через
и обозначается через 
По аналогией с теоремой 5.5 доказывается предложение 6.5
Предложение 6.5. Для произвольного фиксированного вектора  его Ф-орбита
его Ф-орбита  состоит из
состоит из 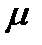 элементов, где
элементов, где  или
или 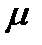 делит
делит  При этом
При этом 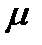 – наименьшее натуральное число с условием
– наименьшее натуральное число с условием 
 а Ф-орбита
а Ф-орбита  имеет следующую структуру:
имеет следующую структуру:  Все векторы из
Все векторы из  имеют одинаковый вес.
имеют одинаковый вес.
Действие группы Ф на векторы пространства Е7иллюстрирует рис. 6.3.

Рис. 6.3. Действие циклотомической подстановки j и ее степеней на пространстве Е7, в частности на вектор 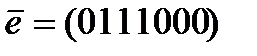
Пример 6.4. Выпишем Ф-орбиты векторов весом 1 в пространстве 



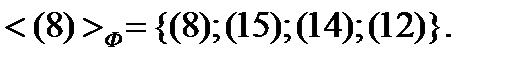
Таким образом, 15 векторов-ошибок весом 1 делятся на 5 Ф-орбит; 3 из них – полные, содержат по 4 вектора, 1 имеет мощность 2, 1 – мощность 1.
Предложение 6.6. Пусть  , где
, где 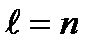 или
или  – делитель
– делитель  , – Г-орбита векторов-ошибок из
, – Г-орбита векторов-ошибок из  , а
, а  . Тогда
. Тогда  – также Г-орбита векторов из
– также Г-орбита векторов из  .
.
Определение 6.7. Пусть  – фиксированная Г-орбита векторов-ошибок из
– фиксированная Г-орбита векторов-ошибок из  . Совокупность всех попарно различных Г-орбит
. Совокупность всех попарно различных Г-орбит  , называется Ф–орбитой класса
, называется Ф–орбитой класса  (или циклоклассом Г-орбиты
(или циклоклассом Г-орбиты  ) при действии
) при действии  на множестве
на множестве 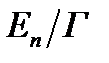 и обозначается
и обозначается  .
.
Теорема 6.6. Для произвольного класса  его Ф-орбита
его Ф-орбита  состоит из
состоит из 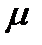 классов, где
классов, где  или
или  делит
делит  . При этом
. При этом  – наименьшее натуральное число с условием
– наименьшее натуральное число с условием  , а
, а  имеет следующую структуру:
имеет следующую структуру:
 . .
| (6.5) |
Определение 6.8. Два вектора  и
и 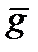 из
из  называются G-эквивалентными, если найдется такая подстановка
называются G-эквивалентными, если найдется такая подстановка  , что
, что  .
.
Очевидно, G – эквивалентные векторы-ошибки должны иметь одинаковый вес. Заметим, что не все векторы-ошибки весом 2 попарно G - эквивалентны. Ведь одному вектору может быть G- эквивалентно не более  других векторов, в силу теоремы 3.4. Векторов-ошибок весом 2 имеется
других векторов, в силу теоремы 3.4. Векторов-ошибок весом 2 имеется  при
при  то есть при
то есть при  что выполняется при всех целых
что выполняется при всех целых 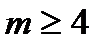 .
.
Определение 6.9. G –орбитой называется совокупность всех попарно G-эквивалентных между собой векторов-ошибок из  .
.
Пусть 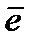 – фиксированный вектор из данной G-орбиты. В силу транзитивности свойства G – эквивалентности эта орбита состоит из векторов пространства
– фиксированный вектор из данной G-орбиты. В силу транзитивности свойства G – эквивалентности эта орбита состоит из векторов пространства  , G – эквивалентных вектору
, G – эквивалентных вектору  . Поэтому G-орбиту с вектором
. Поэтому G-орбиту с вектором  будем иногда обозначать через
будем иногда обозначать через 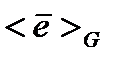 .
.
Предложение 6.7. Пусть 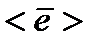 – Г-орбита, порожденная вектором
– Г-орбита, порожденная вектором  . Тогда G-орбита
. Тогда G-орбита 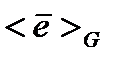 состоит из всех векторов, принадлежащих всем Г-орбитам из
состоит из всех векторов, принадлежащих всем Г-орбитам из  -орбиты
-орбиты  .
.
Пример 6.5. В двоичном пространстве Е31 имеется 15 Г-орбит ошибок веса 2, которые делятся на 3 G -орбиты по 5 Г-орбит в каждой:
 ;
;
 ;
;
 ,
,
145 Г -орбит векторов-ошибок весом 3 (пример 3.5), в свою очередь делящихся на 29 циклоклассов.
|
|
|
|
|
Дата добавления: 2017-02-01; Просмотров: 78; Нарушение авторских прав?; Мы поможем в написании вашей работы!