Необходимые теоретические сведения

Тройных ошибок в БЧХ-кодах

Норменное декодирование

Задания для самостоятельной работы

Задание 1. Взять линейный код из задания №4 раздела «задания для самостоятельной работы» практического занятия №4. Составить таблицу образующих Г-орбит двойных ошибок, синдромов этих образующих и норм вычисленных синдромов.

Задание 2. Задание 5 из раздела «задания для самостоятельной работы» практического занятия №4 решить норменным методом.

Практическое занятие №8

На пути эффективной реализации норменного метода в БЧХ-кодах при коррекции многократных ошибок весом 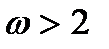стоит препятствие – достаточно большое количество Г-орбит этих ошибок, оцениваемое числом . В [16] установлена формула для числа ошибок с первой компонентой синдрома . Для эта формула гласит: , где длина примитивного БЧХ-кода. Отсюда следует, что количество Г-орбит таких тройных ошибок оценивается числом Это число равно 3 при , пяти – при , 11 – при и так далее.

Рассмотрим модификацию норменного метода, предложенную в [17], которая преобразует векторы ошибок в векторы с , на примере коррекции тройных ошибок.

Исходим из примитивного БЧХ-кода 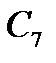длиной с проверочной матрицей где примитивный элемент поля Галуа 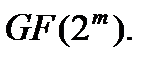Пусть принято сообщение с синдромом ошибок причём . Требуется найти тройную ошибку в принятом сообщении .

Преобразуем искомую вектор-ошибку в другую тройную ошибку , синдром которой имеет первую компоненту Пусть локаторы ошибочных позиций вектора , ненулевых координат вектора В качестве берём вектор-ошибку весом 3 с локаторами ненулевых позиций . Тогда компоненты синдрома выражаются следующим образом через компоненты синдрома :

;

;

.

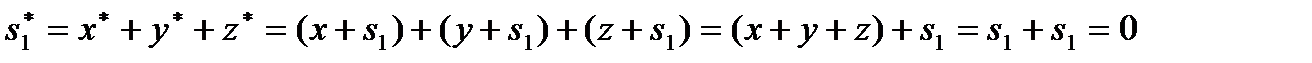Для нахождения вектора-ошибки норменным методом достаточно иметь лишь фрагмент таблицы Г-орбит тройных ошибок, содержащий только Г-орбиты тройных ошибок с .

Пример 8.1. Найдем вектор ошибок модифицированным норменным методом в БЧХ-коде длиной 63 и проверочной матрицей где примитивный элемент поля Галуа , корень полинома , если принято очередное сообщение с синдромом .

Решение. У нас . От искомой ошибки переходим к , у которой компоненты синдрома , , . Таким образом, . Тогда 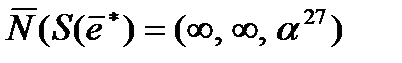. Составим таблицу 8.1.

Таблица 8.1

Составим таблицу 11 Г-орбит тройных ошибок в данном коде с .

№ п/п	Образующая	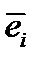Синдром	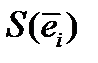Норма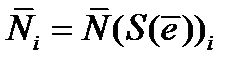

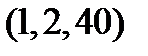
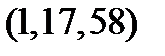
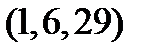
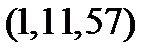
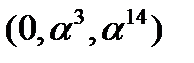
Сравнивая 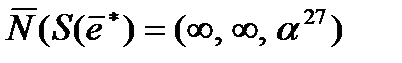с данными таблицы, приходим к выводу, что и получается циклическим сдвигом вектора 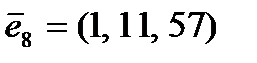. . . . 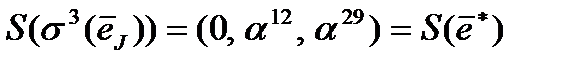Значит, тройная вектор-ошибка с ненулевыми координатами на 4-й, 14-й, 60-й позициях, локаторы которых , . Отсюда легко находятся локаторы ненулевых координат искомого вектора ошибок :

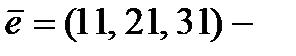; ; . Следовательно, тройная ошибка на 11-й, 21-й и 31-й позициях.

Дата добавления: 2017-02-01