Необходимые теоретические сведения

Векторы каждой Г-орбиты имеют тесную взаимосвязь – каждый из них можно получить циклическими сдвигами любого фиксированного вектора этой Г-орбиты. Подавляющее большинство Г-орбит принадлежит многообразию полных Г-орбит. Такая же тесная связь существует и между синдромами векторов-ошибок каждой Г-орбиты. Об этом свидетельствует

Теорема 7.1. Пусть – вектор ошибок в БЧХ-коде С с проверочной матрицей (5.1). Пусть - синдром ошибок вектора Тогда

(7.1)

а для произвольного целого l синдром

. (7.2)

Если же БЧХ-код задан проверочной матрицей (2.2), то

S (s ())= . (7.3)

Пусть 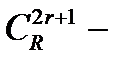реверсивный с проверочной матрицей Тогда

Определение 7.1. Спектром синдромов S(J) в БЧХ-коде С Г-орбиты J называется множество синдромов всех векторов-ошибок из J в этом коде. Спектр S(J) называется полным, если его мощность совпадает с мощностью Г-орбиты J: |S(J)|=| J |, в противном случае спектр S(J) будем называть неполным.

Формулы (7.1) – (7.3) определяют структуру спектра синдромов Г-орбит векторов-ошибок, дают синдромные признаки полноты Г-орбит.

Теорема 7.1 утверждает, что, как и векторы каждой Г-орбиты спектр синдромов можно сконструировать по формулам (7.1) – (7.3) из синдрома любого вектора Здесь, при условии полноты , существует полное взаимно-однозначное соответствие между циклическими сдвигами векторов и соответствующими преобразованиями их синдромов.

Норма синдрома – это векторная характеристика векторов-ошибок, вычисляемая через координаты синдрома.

Определение 7.2. Нормой синдрома вектора ошибок в БЧХ-коде C с проверочной матрицей (5.1) называется вектор с координатами , , которые вычисляются по формулам

а) , если , ; (не существует), если

б) 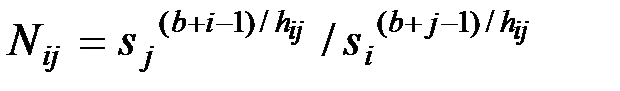, если (7.4)

В двоичном БЧХ-коде с проверочной матрицей (5.2) синдром имеет меньше координат – следовательно, норма синдрома есть вектор с координатами, которые для вычисляются в случае по формуле

. (7.5)

Пусть то есть БЧХ-код задается проверочной матрицей . Тогда норма синдрома состоит из одной компоненты Пусть то есть БЧХ-код задается проверочной матрицей 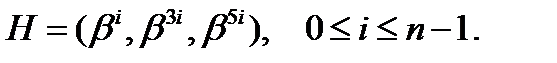Тогда норма синдрома, согласно формуле (7.5), состоит из трех компонент: 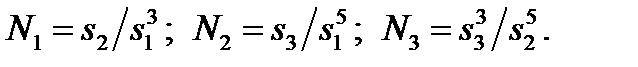Они соответствуют компонентам определения 7.2 при

Определение 7.3. Нормой синдрома 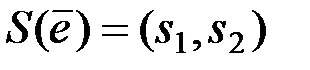вектора-ошибки в реверсивном коде с проверочной матрицей называется величина .

Основное свойство норм синдромов отражает теорема 7.2

Теорема 7.2. Для всякого вектора ошибок и его синдрома в БЧХ-коде справедливо равенство . Это же равенство справедлива и для реверсивных кодов .

Из теоремы 7.2 следует, что все векторы каждой Г-орбиты имеют одинаковую норму синдрома, то есть норма синдрома инвариантна относительно группы Г циклических сдвигов. Это позволяет ввести следующее определение

Определение 7.4. Нормой Г-орбиты J векторов-ошибок в любом БЧХ-коде, а также и в реверсивном коде, называется норма синдрома любого вектора-ошибки из этой Г-орбиты.

Норма Г -орбиты является ее однозначной характеристикой, то есть идентификатором этой орбиты.

Предложение 7.1. Пусть две Г-орбиты векторов-ошибок в БЧХ-коде (в реверсивном коде 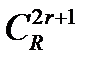), имеющие различные нормы: . Тогда для любых векторов и их синдромы и различны. Другими словами, спектры синдромов таких Г-орбит не пересекаются.

Предложение 7.2. Пусть I и J – две Г-орбиты векторов-ошибок с одинаковыми нормами в примитивном двоичном БЧХ-коде (в реверсивном коде ). Пусть I – полная Г-орбита с полным спектром синдромов. Тогда для всякого вектора найдется вектор ē I, такой, что .

Следствие. Множество Г-орбит всех векторов-ошибок весом 1-3 имеет в примитивном двоичном БЧХ-коде 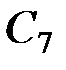попарно различные нормы.Множество Г-орбит всех векторов-ошибок весом 1-2 имеет в примитивном двоичном БЧХ-коде попарно различные нормы.

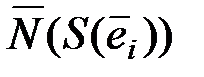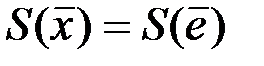Построенная теория позволяет предложить норменный метод коррекции ошибок в БЧХ-кодах. Суть метода. Составляем таблицу всех Г-орбит корректируемых ошибок, таблицу синдромов , а также таблицу . По принятому вектору-сообщению вычисляем и . В таблице норм находим . Тогда вектор . Сравнивая первые компоненты синдромов и , определяем величину циклического сдвига для получения вектора из вектора . Тогда искомый вектор ошибок.

Дата добавления: 2017-02-01