
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Коды Боуза-Чоудхури-Хоквингема, исправляющие двойные ошибки
|
|
|
|
Задания для самостоятельной работы
Задания для аудиторной работы
Задание 1. Проверить на неприводимость следующие полиномы.
1.1)  над полем вещественных чисел и над полем рациональных чисел.
над полем вещественных чисел и над полем рациональных чисел.
1.2.) 
 ,
, 
 над полем
над полем  .
.
1.3.  над полем
над полем 
Задание 2. Исследовать на примитивность над полем 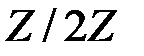 неприводимые полиномы
неприводимые полиномы  ;
; 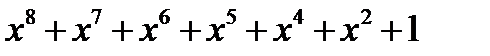 .
.
Решение. Неприводимый полином  степени
степени 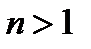 примитивен, если его корень
примитивен, если его корень  является примитивным элементом, то есть образующим циклической группы
является примитивным элементом, то есть образующим циклической группы  . В первых двух случаях это проверяется непосредственно, по аналогии с решением примера 3.5. В третьем случае
. В первых двух случаях это проверяется непосредственно, по аналогии с решением примера 3.5. В третьем случае  и имеет порядок 255. Поэтому здесь следует воспользоваться программными средствами. Можно также воспользоваться следующим признаком примитивности элемента в циклической группе.
и имеет порядок 255. Поэтому здесь следует воспользоваться программными средствами. Можно также воспользоваться следующим признаком примитивности элемента в циклической группе.
Пусть  циклическая группа порядка
циклическая группа порядка  . Если элемент
. Если элемент  обладает свойствами: для каждого целого
обладает свойствами: для каждого целого  и целого
и целого  степень
степень  , то
, то  элемент
элемент  является образующей группы
является образующей группы  .
.
В данном случае  ,
,  ;
;  ;
;  . Величина
. Величина  есть результат подстановки
есть результат подстановки  в остаток от деления
в остаток от деления  на
на  . Вычисления показывают, что
. Вычисления показывают, что  . Аналогично,
. Аналогично,  ;
;  .
.
Проведенные вычисления показывают, что неприводимый полином 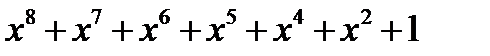 является примитивным.
является примитивным.
Задание 3. Исследовать на примитивность над полем  неприводимые полиномы
неприводимые полиномы 
Задание 4. На основе полинома  построить полиномиальное, мультипликативное и двоичное векторное задание поля Галуа из 8 элементов.
построить полиномиальное, мультипликативное и двоичное векторное задание поля Галуа из 8 элементов.
Задание 5. На основе полинома  построить полиномиальное, мультипликативное и двоичное векторное задание поля Галуа из 16 элементов.
построить полиномиальное, мультипликативное и двоичное векторное задание поля Галуа из 16 элементов.
Задание 6. На основе полинома  построить полиномиальное, мультипликативное и двоичное векторное задание поля Галуа из 9 элементов.
построить полиномиальное, мультипликативное и двоичное векторное задание поля Галуа из 9 элементов.
Задание 7. Сформировать матрицу 
 кода Хемминга, где
кода Хемминга, где 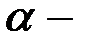 корень полинома
корень полинома  . Найти порождающую матрицу этого кода.
. Найти порождающую матрицу этого кода.
Задание 8. Содержит ли ошибки сообщение  принятое
принятое  кодом Хемминга.
кодом Хемминга.
Задание 9. Указать ошибку в сообщении  и устранить её. Выписать исправленное сообщение.
и устранить её. Выписать исправленное сообщение.
Задание 10. Сформировать матрицу 
 кода Хемминга, где
кода Хемминга, где 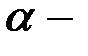 корень полинома
корень полинома  . Содержит ли ошибки сообщение
. Содержит ли ошибки сообщение  принятое этим кодом. Указать ошибку в сообщении
принятое этим кодом. Указать ошибку в сообщении  и устранить её. Выписать исправленное сообщение.
и устранить её. Выписать исправленное сообщение.
Задание 11. Сформировать матрицу  непримитивного
непримитивного  кода Хемминга, где
кода Хемминга, где  и
и 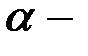 корень полинома
корень полинома 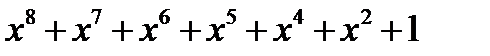 .
.
Решение.  .
.
Задание 1. Доказать неприводимость полинома 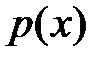 над
над  (по вариантам).
(по вариантам).
Задание 2. Проверить полином 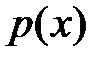 на примитивность.
на примитивность.
Задание 3. С помощью корня  полинома
полинома 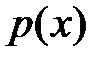 построить проверочную матрицу
построить проверочную матрицу  не примитивного (17, 9) – кода Хемминга.
не примитивного (17, 9) – кода Хемминга.
Задание 4. С помощью построенной матрицы  найти минимальное расстояние (17, 9) – кода Хемминга.
найти минимальное расстояние (17, 9) – кода Хемминга.
Вариант 1. 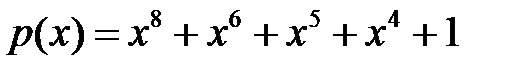 .
.
Вариант 2.  .
.
Вариант 3.  .
.
Вариант 4.  .
.
Вариант 5.  .
.
Вариант 6.  .
.
Вариант 7.  .
.
Вариант 8.  .
.
Вариант 9.  .
.
Вариант 10.  .
.
Вариант 11. 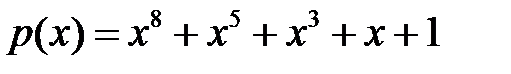 .
.
Вариант 12.  .
.
Вариант 13.  .
.
Вариант 14.  .
.
Вариант 15.  .
.
Практическое занятие №4
|
|
|
|
|
Дата добавления: 2017-02-01; Просмотров: 78; Нарушение авторских прав?; Мы поможем в написании вашей работы!