Необходимые теоретические сведения 1 страница

Аутентичные коды Хемминга появились еще в 40-х годах ХХ века – в период зарождения помехоустойчивого кодирования. Задаются они достаточно просто. Произвольный код Хемминга – это линейный код длиной для некоторого целого , имеющий размерность , который задается проверочной матрицей , где двоичная разрядная запись целого числа в столбец. Такое задание кода называют лексикографическим. Ясно, что все столбцы матрицы – ненулевые и попарно различные. При этом . Следовательно, код Хемминга имеет минимальное расстояние 3 и исправляет одиночные ошибки. Предыдущее занятие позволяет нам успешно исправлять их синдромным методом.

Количество синдромов в коде Хемминга в точности равно количеству исправляемых им ошибок. По этому свойству коды Хемминга относят к разряду совершенных кодов. Еще коды Хемминга относят к классу примитивных БЧХ-кодов.

Примитивные коды Хемминга служат основой для построения других классов кодов с минимальным расстоянием , с интересными свойствами и более широкими декодирующими возможностями. Но для реализации таких возможностей необходимо перейти к иной, более современной интерпретации проверочных матриц кодов Хемминга – на языке полей Галуа. А для этого потребуется дальнейшее погружение в современную математику.

Термин «поле» имеет в науке различные толкования. Мы осведомлены о скалярных и векторных полях, физика поставляет нам их материальные интерпретации в виде электромагнитных, гравитационных полей и т.п.

Алгебра дает совершенно иную интерпретацию термину «поле». Здесь имеет место определение 3.1.

Определение 3.1. Полем называется любое ассоциативное и коммутативное кольцо с 1, в котором всякий ненулевой элемент имеет обратный относительно умножения.

Данное определение для своего понимания требует усвоения комплекса понятий из теории колец. В силу определения 3.1 всякое поле не имеет делителей нуля (так как они не могут иметь обратных элементов), не имеют собственных идеалов (так как все собственные идеалы порождаются элементами, не имеющими обратных). По-существу, поле – множество, в котором можно осуществлять четыре арифметические действия: сложение, вычитание, умножение, деление.

Мы прекрасно освоились с полями рациональных чисел , вещественных чисел , комплексных чисел . Сейчас к ним добавились конечные поля 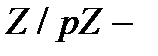кольца классов вычетов по простому модулю . Конечные поля не исчерпываются перечисленными. Все остальные конечные поля строятся факторизацией колец полиномов 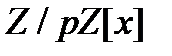по тем или иным собственным максимальным идеалам. Об этом следует поговорить более подробно.

Определение 3.2. Кольцом называется непустое множество с двумя бинарными алгебраическими операциями сложения (+) и умножения (·); относительно операции сложения является абелевой группой, а умножение и сложение связаны законами дистрибутивности: ; для произвольных .

Во всяком ассоциативном (относительно умножения) нетривиальном кольце с единицей (нейтральным элементом относительно умножения) , иначе кольцо состоит из элемента .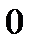

В дальнейшем будем иметь дело с ассоциативными коммутативными (относительно умножения) кольцами с единицей, содержащими более одного элемента. Наиболее популярные примеры таких колец: кольцо целых чисел 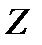, кольцо классов вычетов , кольцо полиномов с коэффициентами из произвольного поля .

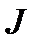Определение 3.3. Подкольцо кольца это подгруппа аддитивной группы которая, в свою очередь, является кольцом относительно операций в кольце то есть подгруппа, замкнутая относительно умножения, определенного в кольце Подкольцо коммутативно гокольца называется идеалом этого кольца, если для любого и для каждого 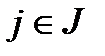произведение то есть

Среди подколец наибольший интерес представляют идеалы. В любом кольце К множества {0} и K формально также являются идеалами кольца K. Их называют несобственными или тривиальными в отличие от остальных – собственных идеалов.Отметим основные свойства идеалов.

Теорема 3.1. Пересечение идеалов данного кольца есть идеал этого же кольца. Произведение идеалов кольца есть идеал этого же кольца. Для каждого элемента a кольца множество есть идеал кольца . Если в кольце c единицей элемент обратим относительно умножения, то ; если же ненулевой и необратимый элемент кольца , то собственный идеал кольца . Если для не обратимых элементов , то , .

Приведенный в теореме 3.1 идеал называется главным идеалом кольца , порожденным элементом . Известно, что в кольце целых чисел каждый идеал является главным. То же самое справедливо и для кольца полиномов с коэффициентами из произвольного поля .

На множестве идеалов каждого кольца существует отношение частичного порядка по включению их друг в друга как множеств. Особую роль играют максимальные идеалы.

Определение 3.4. Идеал кольца называется максимальным, если в не существует соответствующего собственного идеала с условием

Теория колец даёт чёткое описание максимальных идеалов в кольце целых чисел и в кольце полиномов. В кольце целых чисел 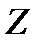идеалы и связаны отношением включения тогда и только тогда, когда делится на 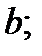идеал является максимальным тогда и только тогда, когда простое число.

Теорема 3.2. В кольце полиномов с коэффициентами из поля 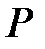идеал максимален тогда и только тогда, когда порождающий его полином неприводим над полем

Главное качество максимальных идеалов выражает следующая теорема.

Теорема 3.3. Фактор-кольцо 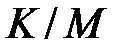ассоциативного и коммутативного кольца с единицей по максимальному идеалу есть поле.

Пример 3.1. Возьмем в кольце полиномов c коэффициентами из поля произвольный собственный идеал 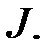Как отмечалось выше, он является главным идеалом: для некоторого полинома степени Фактор-кольцо состоит из смежных классов по модулю . В один класс смежности по модулю попадают те и только те полиномы, разность которых делится на 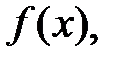то есть те, которые имеют один и тот же остаток от деления на Отсюда следует, что фактор-кольцо состоит из классов где степень меньше степени полинома

Рассмотрим конкретный пример.

Пример 3.2. Пусть в примере 3.1 В кольце имеется, как не трудно заметить, в точности различных полиномов степени, меньшей Поэтому для полинома степени фактор-кольцо конечно и состоит из элементов, определяемых всевозможными полиномами степени, меньшей 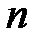. Операции сложения и умножения в этом кольце можно задать конкретно в виде таблиц.

Пример 3.3. Кольцо состоит из смежных классов , , 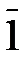, 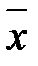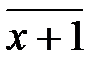.Напишем таблицы сложения и умножения в этом кольце.

Å

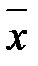
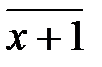
Ä

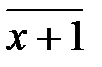
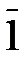
Из таблицы умножения следует, что в кольце все ненулевые элементы обратимы относительно умножения, то есть Следовательно, поле из четырёх элементов.

Итак, фактор-кольца по максимальным идеалам являются источником новых полей, в частности конечных полей. Выясним, насколько общий характер имеют эти примеры в общей теории полей.

Всякое поле имеет либо нулевую, либо ненулевую характеристику.

Определение 3.5. Если в поле существует такое натуральное что равна нулю сумма единиц ( раз складывается с самим собой нейтральный элемент относительно умножения): то наименьшее с таким свойством называется характеристикой поля и обозначается через Если в поле любая конечная сумма единиц отлична от нуля, то говорят, что характеристика поля равна 0.

Теорема 3.4. Если характеристика поля отлична от нуля, то она является числом простым.

Пример 3.4. В поле 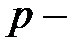простое число, характеристика равна 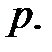Поля имеют, очевидно, характеристику 0.

Определение 3.6. Поле называется подполем поля если все его элементы принадлежат полю

Теорема 3.5. Если подполе поля 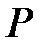имеет характеристику то и поле имеет ту же характеристику. Все подполя поля имеют ту же характеристику, что и поле .

Со школьной скамьи мы привыкли к полям характеристики 0. С их точки зрения арифметика полей положительной характеристики весьма экзотична.

Теорема 3.6. Пусть произвольное поле положительной характеристики Пусть произвольное целое число и остаток от деления на Тогда для каждого элемента имеет место равенство 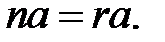В частности, при произведение Если то при произведение а при произведение Для любых а для каждого целого

На многообразии всех подполей данного поля определено отношение частичного порядка по включению, обладающее свойством транзитивности.

Определение 3.7. Минимальным, или простым, называется поле, не содержащее собственных подполей.

Теорема 3.7. Поле рациональных чисел 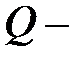минимальное поле характеристики 0; – минимальное поле характеристики Следовательно, в любом поле 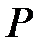имеется в точности одно минимальное подполе, изоморфное либо либо в зависимости от характеристики поля .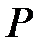

Определение и основные свойства векторных пространств над полем R переносятся на произвольные поля. При этом векторное пространство над конечным полем имеет свои особенности.

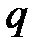Теорема 3.8. Пусть мерное линейное пространство над полем из элементов. Тогда состоит из векторов.

Определение 3.8. Если 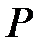является подполем поля то называют расширением поля .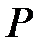

Очевидно, любое расширение произвольного поля является векторным пространством над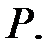

Определение 3.9. Расширение поля называется конечным степени , если размерность векторного пространства над полем 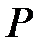конечна и равна . Степень расширения принято обозначать через

Дата добавления: 2017-02-01