Необходимые теоретические сведения

Понятие линейного кода – одно из первичных, базовых понятий теории и практики помехоустойчивого кодирования. Сформировалось в теории информации к середине ХХ века. Аккумулирует в себе достаточно широкую научно-философскую концепцию.

Формальное математическое определение кода выглядит загадочным.

Определение 1.1. Линейным 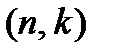кодом над полем 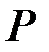называется произвольное 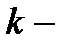мерное подпространство линейного пространства 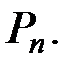Параметр 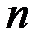называется длиной кода, а 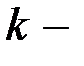размерностью кода. Линейный код называется высокоскоростным, если отношение 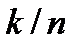близко к 1, и низкоскоростным, если отношение 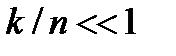близко к нулю.

Данное определение явно требует пояснений. В современных цифровых инфокоммуникационных системах (ИКС) принято передаваемую информацию задавать в виде блоков – конечных последовательностей фиксированной длины символов из данного поля 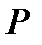. Другими словами, всякое информационное слово представляет собой k –разрядный вектор – произвольный вектор из k –мерного линейного пространства 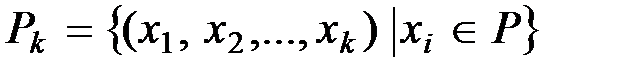для заданного целого 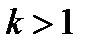. Поэтому такая форма представления информации кодированием не считается. Главная цель кодирования – обеспечить надежную передачу информации в каналах с шумами, то есть помехами. Малейшее изменение слова-вектора 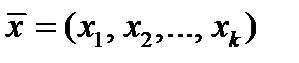приводит к другому информационному вектору 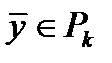. Согласно базовой идее Шеннона К. успешную борьбу с помехами в каналах с шумами можно осуществлять искусным введением избыточности в передаваемую информацию.

Теорема 1.1 (Шеннон К., 1948 г.). Введением избыточности в передаваемую в зашумлённом канале связи информацию можно добиться исправления возникающих в процессе передачи этой информации сколь угодно сложных ошибок.

Удачно наделенный избыточностью, каждый вектор-сообщение приобретает настолько специфические индивидуальные свойства, что даже после прохождения в каналах с шумами, после наложения искажений остается возможность этот вектор, то есть исходную передаваемую информацию, однозначно восстановить.

Идея Шеннона получила различные интерпретации и реализации. Наиболее простой и наиболее популярной оказалась реализация идеи Шеннона линейными кодами.

В линейных кодах избыточность достигается введением искусных поразрядных, то есть покоординатных проверок: к каждому информационному слову-сообщению 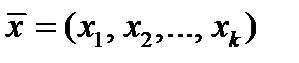добавляются 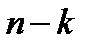координат-разрядов; координаты 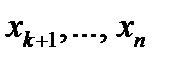таковы, что их специально подобранные алгебраические суммы с предыдущими координатами в неискаженном состоянии принимают строго фиксированные (обычно, нулевые) значения.Удлиненные таким образом векторы принято называть кодовыми. Код – совокупность всех кодовых векторов, получаемых при заданном способе кодирования.

С математической точки зрения рассмотренное преобразование есть линейное отображение линейного пространства 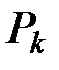в пространство большей размерности 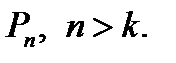Из курса линейной алгебры следует матричное задание линейных отображений векторных пространств. Следовательно, кодирование есть, по сути дела, умножение информационных слов-векторов на некоторую матрицу порядка 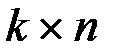с коэффициентами из поля .

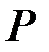Поясним этот момент более детальными сведениями из линейной алгебры. Если оговорено или из контекста ясно, с какими базисами этих пространств мы имеем дело, то линейный оператор 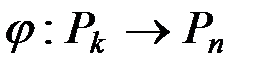однозначно определяется матрицей 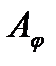этого оператора в данных базисах. Пусть 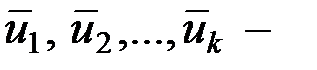базис пространств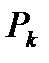а , а 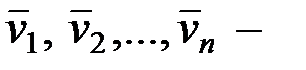базис пространства . Векторы 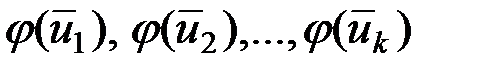разложим по этому базису пространства . Полученные в результате разложения координаты векторов 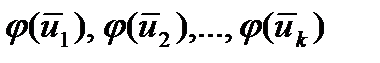составляют столбцы матрицы 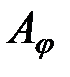. Как известно, для всякого вектора 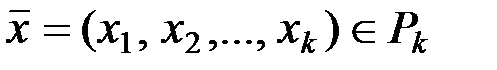вектор-столбец 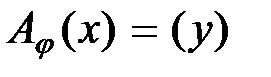, где 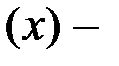столбец из координат вектора 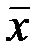, состоит из координат вектора 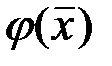в базисе 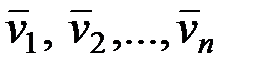пространства 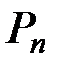. Применив операцию траспонирования к равенству 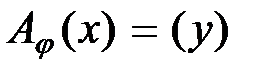, получим более точное соотношение: 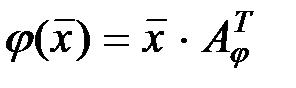. Таким образом, из сказанного выше следует, что матрица .

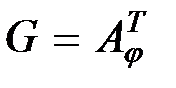Получаемые в результате умножения векторов пространства 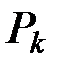на матрицу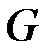 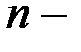разрядные векторы – векторы из пространства 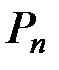– называются кодовыми словами. В общей совокупности они образуют k –мерное подпространство 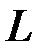в линейном пространстве 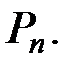Таким образом, получен линейный 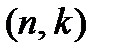код 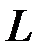над полем 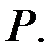Здесь 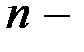длина, а 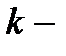размерность кода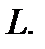

Пример 1.1. С середины ХХ века долгое время в американских системах цифровой связи передача данных осуществлялась в так называемом ASCII-формате. Этот формат требовал передавать данные блоками по 8 двоичных бит, 7 из них были информационными, а 8-й был проверочным, в нём записывался 0 или 1 так, чтобы во всём байте, то есть во всём блоке, сохранялось чётное число единиц. Таким образом, восьмой бит осуществлял проверку на чётность во всём байте – все восемь координат 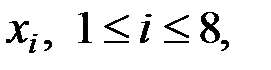байта в совокупности удовлетворяли над полем Галуа 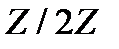из двух элементов линейному однородному уравнению:

.

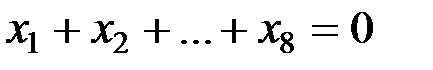Согласно одному из фундаментальных результатов линейной алгебры, множество решений любой однородной системы уравнений от 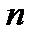неизвестных с коэффициентами из поля 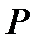образует подпространство в пространстве 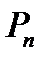, причём размерность подпространства решений равна , где 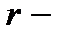ранг матрицы 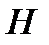коэффициентов системы. В линейной алгебре данное подпространство называют ядром матрицы 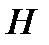и потому обозначают через 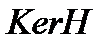(от английского kernel – ядро).

Множество решений данного однородного уравнения представляет весь спектр векторов-слов ASCII-формата. В соответствии с отмеченным выше результатом, эти решения – двоичные векторы 8-мерного пространства 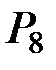над полем Галуа 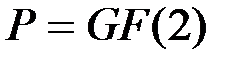из двух элементов – образуют в 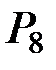7-мерное подпространство 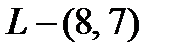линейный код над полем из двух элементов. Легко видеть, что Ф.С.Р. – базис пространства 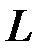решений данного уравнения – образуют следующие 7 векторов: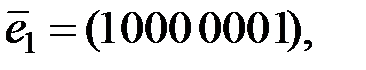 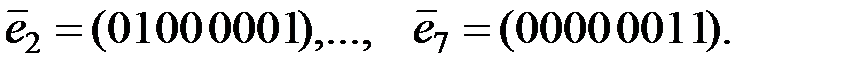Пусть 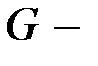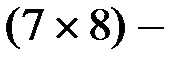матрица, строки которой состоят из координат векторов :

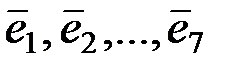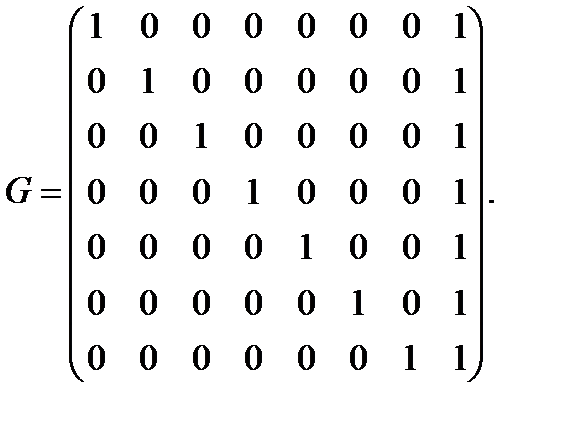(1.1)

Умножением произвольных 7-мерных информационных двоичных векторов на матрицу 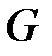мы преобразуем их в ASCII-формат.

Пример 1.2. Очевидно, пример 1.1 имеет прозрачное обобщение на коды любой длины. Это двоичные, как и в примере 1.1, коды. Каждое кодовое слово получается добавлением к информационным блокам длиной 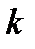единственного 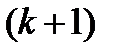проверочного разряда, в нём записывается 0 или 1 так, чтобы во всём блоке сохранялось чётное число единиц. Здесь 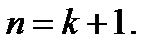Такие коды называют кодами с проверкой на чётность. Будем их в дальнейшем обозначать символом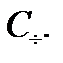

Осмысление примера 1.1, точнее факта реальной послевоенной жизни США Клодом Шенноном, привело к формулировке его знаменитой теоремы 1.1., выражающей главную цель и назначение помехоустойчивых кодов.

Этот же пример привел Роберта Хемминга – современника и соотечественника К. Шеннона – к созданию конкретных основ помехоустойчивого кодирования. Первым шагом в этом направлении было развитие примера 1.2. Это развитие отражено в следующем примере.

Пример 1.3. Пусть 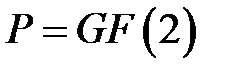– поле Галуа из двух элементов; 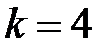, то есть передаваемая информация состоит из 4–мерных векторов 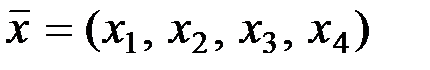с координатами 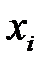, , 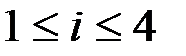со значениями 0,1 из поля 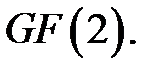Каждый вектор 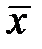кодируем, присоединив к нему координаты , 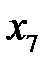вычисленные по следующим правилам: 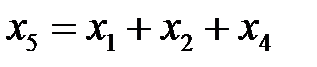, , 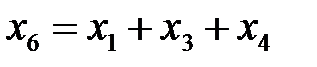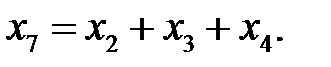Тем самым получим линейный код , состоящий из векторов 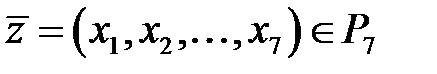, удовлетворяющих проверочным соотношениям:

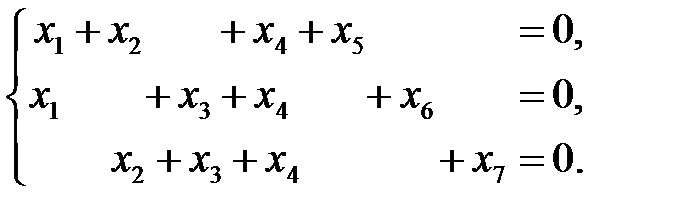(1.2)

Пусть 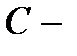линейный 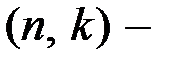код над полем 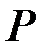. Пусть 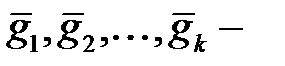базис кода .

Определение 1.2. Порождающей матрицей кода называется 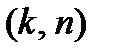матрица 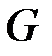, строки которой состоят из координат базисных векторов 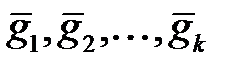кода 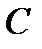в заданном базисе пространства .

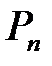Из примера 1.1 следует, что матрица (1.1) является матрицей 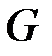, порождающей ASCII-формат.

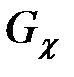
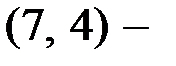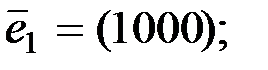
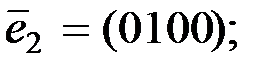
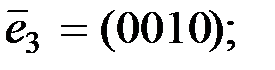
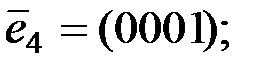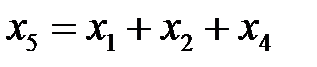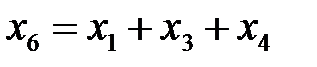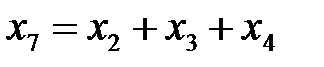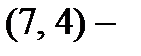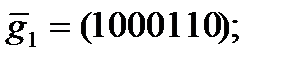
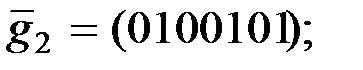
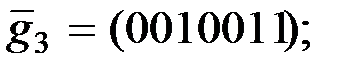
Построим порождающую матрицу кода Хемминга из примера 1.3. В двоичном четырёхмерном пространстве возьмём стандартный базис В соответствии с формулами , , из этого базиса получаем базис кода Хемминга: Следовательно,

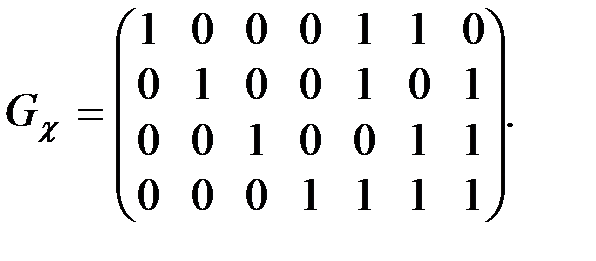
Отметим основные свойства проверочных матриц. Из определения 1.2 непосредственно следуют следующие свойства.

Свойство 1. Порождающая матрица 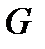линейного 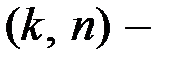кода является прямоугольной 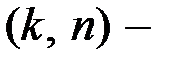матрицей, где 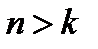, ранг которой равен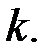

Значение 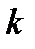возникает из требований на соответствие размеров перемножаемых векторов и матриц. Условие 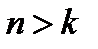обеспечивает избыточность – наличие «дополнительных, проверочных» 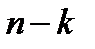разрядов. В силу условия 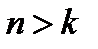ранг матрицы 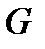не может быть больше 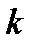. Условие 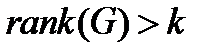неизбежно повлекло бы за собой наличие информационых векторов с одинаковыми «кодировками». Только условие 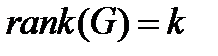обеспечивает инъективность операции кодирования: различным информационным словам соответствуют различные кодовые слова.

Название порождающей матрицы объясняет свойство 2.

Свойство 2. Любое кодовое слово линейного кода является линейной комбинацией строк матрицы .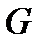

Здесь следует вспомнить, что базисов в любом нетривиальном пространстве достаточно много. Поэтому из определения 1.2 вытекает свойство 3.

Свойство 3. Порождающая матрица кода определена не однозначно.

Любая телекоммуникационная система (ТКС), функционирующая на основе конкретного помехоустойчивого линейного кода 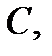на своей передающей части должна иметь фиксированную порождающую матрицу 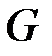этого кода. Данные, поступающие в ТКС от источника данных, обрабатываются кодером источника: разбиваются на компактные блоки, которые преобразуются в стандартные последовательности символов, – кодовые слова источника. Это информационные слова – векторы из k –мерного пространства 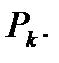Каждое информационное кодовое слово 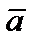источника преобразуется кодером канала в другую, более длинную последовательность символов 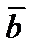, содержащую в себе некоторую избыточность, называемую кодовым словом канала. В линейных кодах этот переход определяет следующее свойство.

Свойство 4. Всякое информационное слово 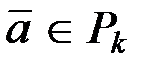и порождаемое им кодовое слово 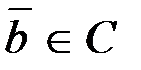связаны соотношением

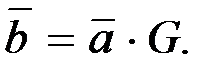(1.3)

Пример 1.4. Закодируем 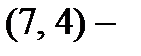кодом Хемминга информационное слово 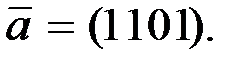Согласно формуле (1.3)

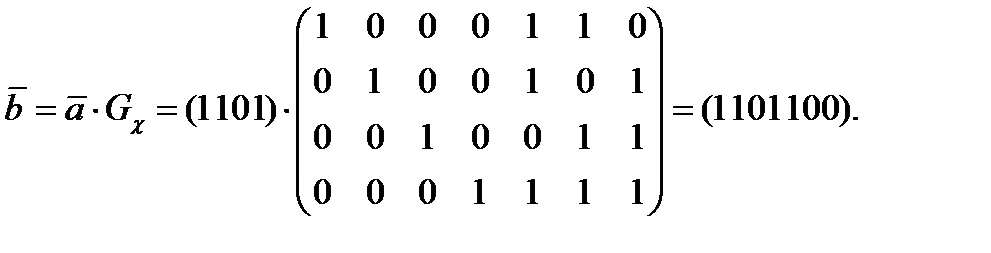
Корректность перехода, задаваемого формулой (1.3), то есть однозначность восстановления 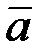по заданному 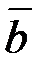,гарантирует теорема 1.2.

Теорема 1.2. Отображение 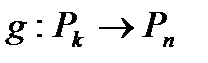по формуле (1.3) с 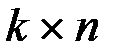матрицей 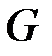ранга 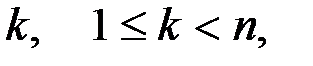и с коэффициентами из поля 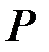является взаимно-однозначным (биекцией).

Свойство 5. По известному кодовому вектору 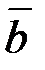при заданной матрице 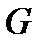исходный информационный вектор 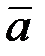однозначно восстанавливается.

Доказательство. Пусть 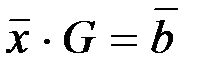для неизвестного вектора 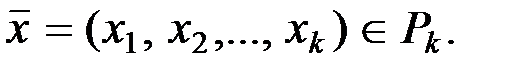Векторно-матричное равенство 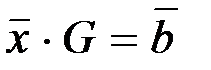есть система из 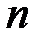линейных уравнений от 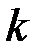неизвестных 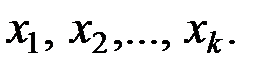По построению матрицы 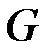ранг её равен 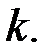Это говорит о наличии в матрице 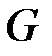ненулевого минора 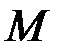порядка 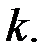Согласно общей теории линейных уравнений, рассматриваемая система эквивалентна подсистеме из тех уравнений, коэффициенты которых вошли в минор 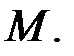А это крамеровская подсистема, определитель которой 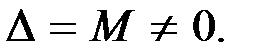Такая система, согласно правилу Крамера, имеет единственное решение.

Замечание. Доказательство следствия конструктивно даёт непосредственный алгоритм восстановления исходной информации.

Пример 1.5. В 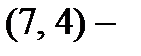коде Хемминга по принятому кодовому слову 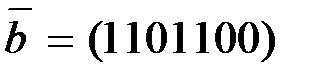из примера 1.5 восстановим исходное информационное слово. Для этого выпишем явно систему линейных уравнений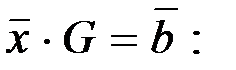

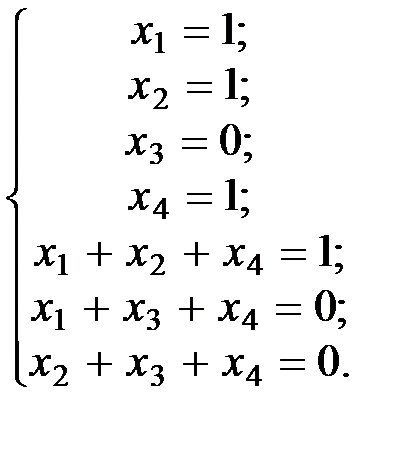
Данная система эквивалентна своей подсистеме из первых четырёх уравнений, которая однозначно указывает, что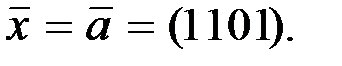

Дата добавления: 2017-02-01