Неприводимые полиномы. Поля Галуа и коды Хемминга

Задания для самостоятельной работы

Задания для аудиторной работы

Задание 1. Дана порождающая 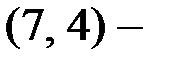код матрица 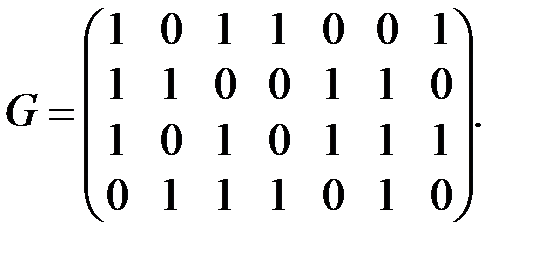Найти проверочную матрицу этого кода. Однозначно ли она определена?

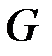Решение. Проверочная и порождающая матрицы и (соответственно) всякого линейного кода связаны соотношениям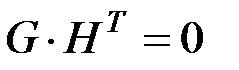и: и 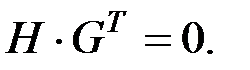При этом размерности этих матриц взаимно-дополнительны: если 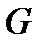является 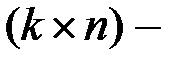матрицей, то 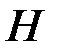является матрицей. Из этих фактов следует, что строки матрицы 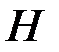составлены из координат ядра матрицы 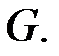Следовательно, надо найти Ф.С.Р. – базис пространства решений однородной СЛАУ 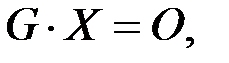где 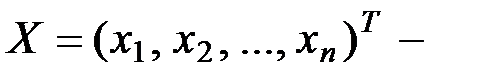столбец неизвестных, а затем из координаты векторов базиса пространства решений выписать в строки матрицы 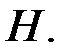Выпишем систему 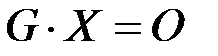в матричной форме: 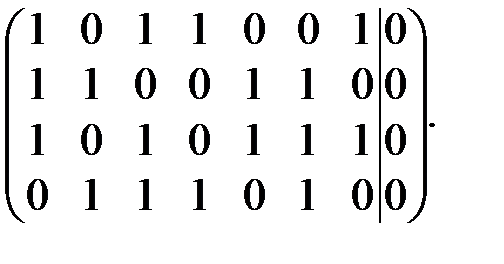Решим систему методом Гаусса. Элементарные преобразования строк приводят систему к виду

Система приведена к квазидиагональному виду.
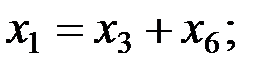
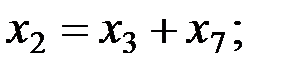
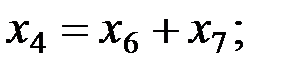
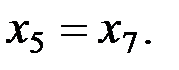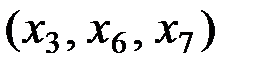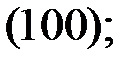
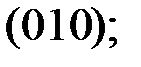
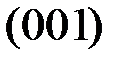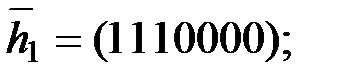
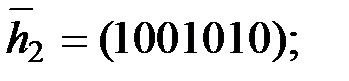
В ней, очевидно, базисными переменными являются 1-я, 2-я, 4-я и 5-я, а свободными – 2-я, 6-я и 7-я. При этом Значит, размерность пространства решений равна трём. Придавая тройке свободных переменных последовательно значения , получим искомый базис пространства решений СЛАУ: 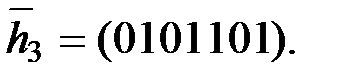Следовательно, матрица 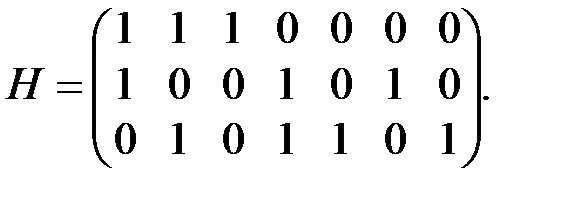Матрица 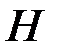определена неоднозначно, поскольку тройка 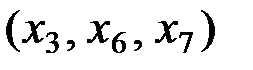может принимать достаточно широкий спектр значений: каждая тройка значений должна быть линейно независимой – определитель, составленный из каждой такой тройки должен быть отличным от нуля.

Задание2. Построить проверочную матрицу кода по заданной порождающей матрице 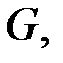если эта матрица имеет вид

а) 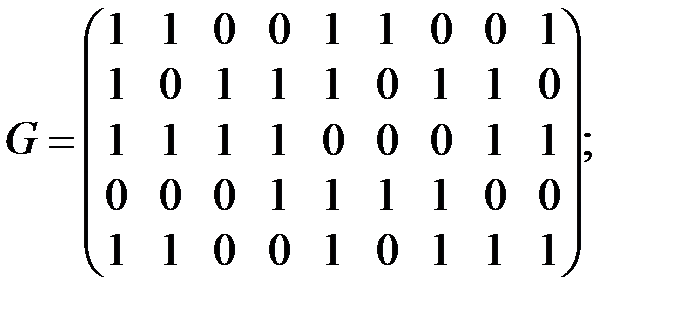б)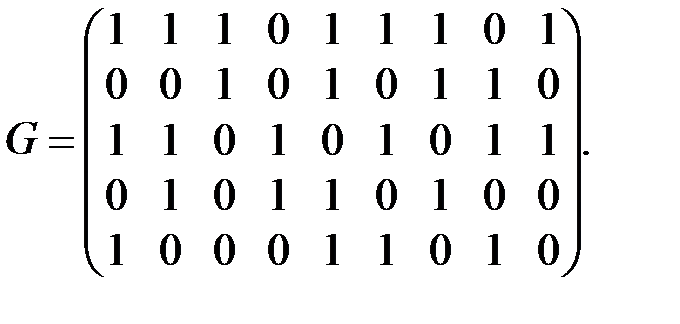

Задание3. Найти расстояние Хемминга между векторам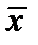и и 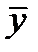, если

а) 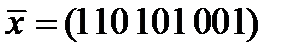, 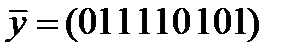; б) , .

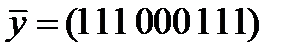Задание4. Определить декодирующие возможности линейного кода, заданного проверочной матрицей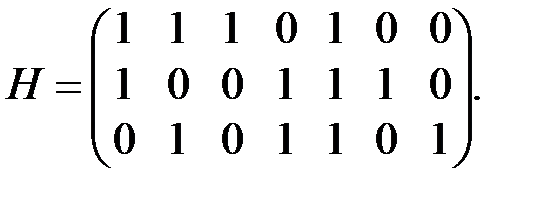

Решение. Декодирующие возможности линейного кода определяются его минимальным расстоянием – минимальным весом 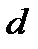кодовых слов этого кода: ес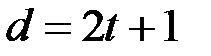ли или 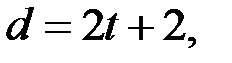то код способен исправлять векторы-ошибки весом 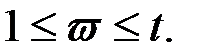Параметр 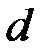определяется по проверочной матрице кода: если у проверочной матрицы 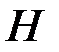данного кода любые 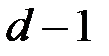столбцов линейно независимы, но найдутся 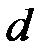линейно зависимых столбцов, то минимальное расстояние кода равно .

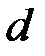В данном случае любые два столбца неодинаковы и, следовательно, линейно независимы над полем 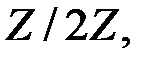но найдутся три линейно зависимых столбца. Например, сумма второго, третьего и седьмого столбцов данной матрицы 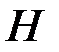равна нулю, иными словами, линейная комбинация этих столбцов равна нулю. Короче говоря, эти три столбца линейно зависимы. Следовательно, 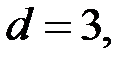данный код способен корректировать одиночные ошибки.

Задание5. Найти все кодовые слова кода 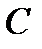, заданного матрицей 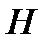из задания 4. Составить таблицу распределения весов кодовых слов. Убедиться непосредственно, что минимальное расстояние кода действительно равно 3.

Задание6. Определить декодирующие возможности линейного кода, заданного проверочной матрицей 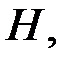если эта матрица имеет вид

а) 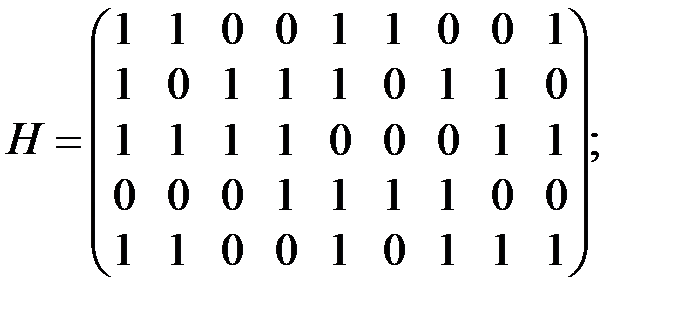б)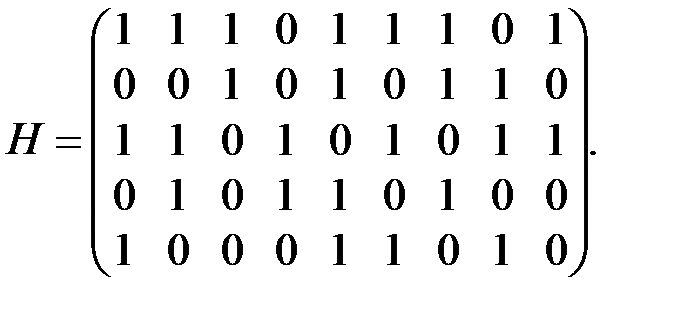

Задание7. ТКС функционирует на основе линейного кода, заданного проверочной матрицей 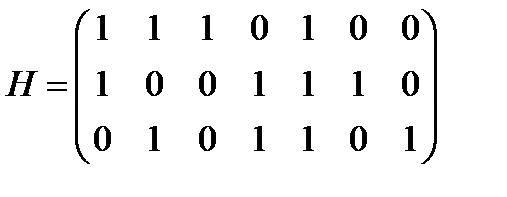(из задания 3). ТКС приняла сообщение 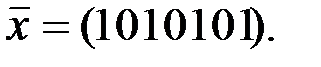Определить наличие ошибок в этом сообщении.

Решение. О наличии или отсутствии ошибок в принятом сообщении свидетельствует синдром ошибок 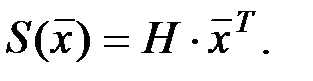Если 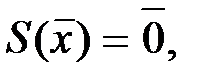то сообщение 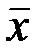не содержит ошибок, если же 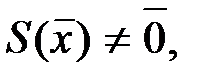то сообщение 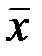содержит ошибки. В данном случае

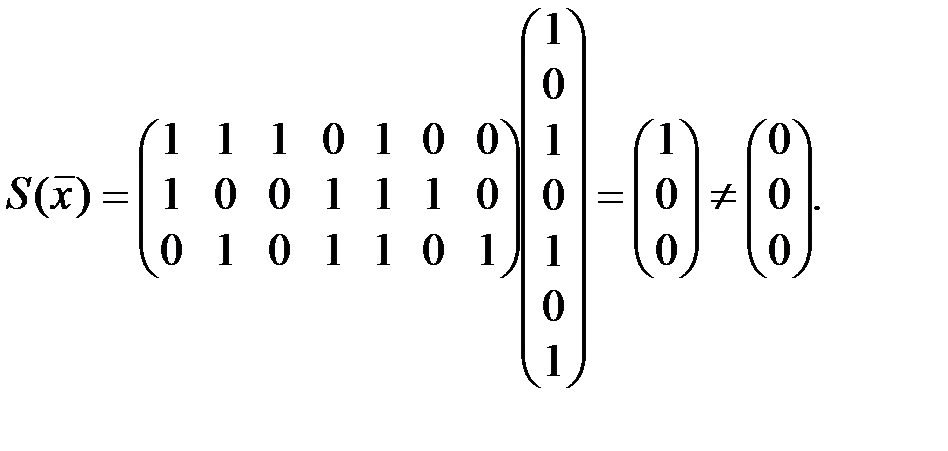
Следовательно, принятое сообщение содержит ошибки.

Задание8. Что можно сказать о векторе-ошибке в задании 7, если ее вес равен 1? Можно назвать истинное сообщение?

Решение. Как известно, сообщени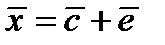е , где 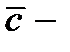передаваемое кодовое слово, 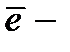искомый вектор-ошибка. 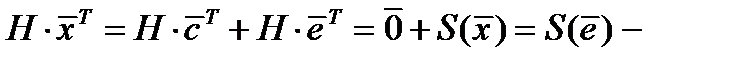сумма столбцов матрицы 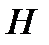, соответствующих ненулевым координатам вектора 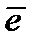. Если вес вектора-ошибки 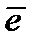равен 1, то 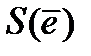равен столбцу матрицы 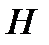, который соответствует ошибочной позиции. В данном случае видим, что ошибка произошла на третьей позиции. Значит, истинное сообщение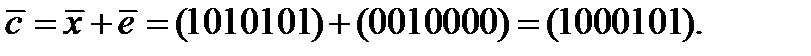

Задание9. Содержит ли ошибки сообщение 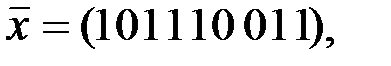если оно получено приёмным устройством ТКС на основе линейного кода с проверочной матрицей из задания 6.Что можно сказать о весе ошибки – вес, возможно, равен 1, или же можно утверждать, что вес ошибки больше 1?

1. Взять матрицу 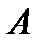из заданий для самостоятельной работы ПЗ1 (по вариантам) в качестве проверочной матрицы соответствующего линейного кода . Найти порождающую матрицу этого кода.

2. Найти все кодовые слова кода и их веса. Составить таблицу распределения весов кода . Указать минимальное расстояние кода .

3. Найти минимальное расстояние кода , вычисляя ранги систем столбцов проверочной матрицы 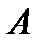этого кода.

4. Среди кодовых слов кода найти вектор 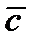весом 5. Из этого вектора получить три вектора-сообщения: 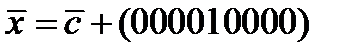; ; 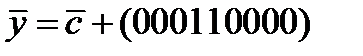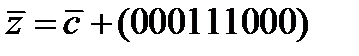. Найти синдромы ошибок этих трех сообщений.

5. Имея в наличии матрицу 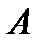и синдромы 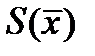; ; 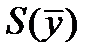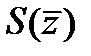, высказать суждение о весах ошибок в принятых сообщениях 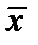, , 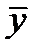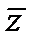. Можно ли исправить ошибки в принятых сообщениях?

Практическое занятие №3

Дата добавления: 2017-02-01