Проверочная матрица линейного кода. Метрика Хемминга. Синдромы ошибок

Задания для самостоятельной работы

Задания для аудиторной работы

Задание1. Выяснить, может ли двоичная матрица 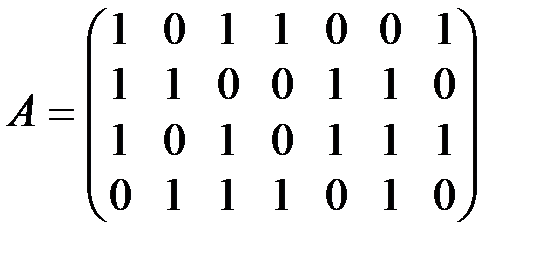быть порождающей матрицей линейного кода?

Решение. Известно, что у прямоугольной 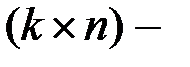матрицы 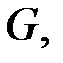порождающей линейный 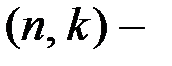код, ранг равен 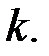В нашем случае матрица 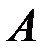имеет порядок 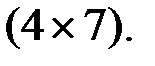Найдём её ранг методом элементарных преобразований. С помощью элементарных преобразований строк данную матрицу можно привести к следующему квазитреугольному виду: 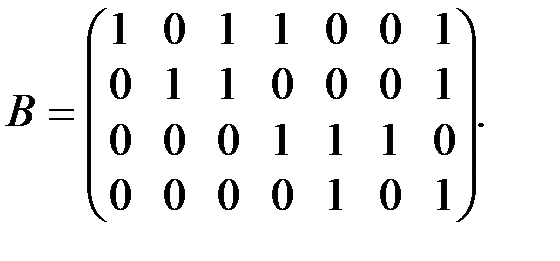Минор порядка 4 матрицы 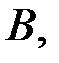состоящий из 1-го, 2-го, 4-го и 5-го столбцов, очевидно равен 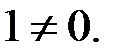Следовательно, 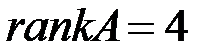и матрицу 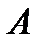можно взять в качестве порождающей матрицы линейныого кода.

Задание2. Выяснить тот же вопрос (из задания 1) для матрицы 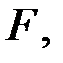где

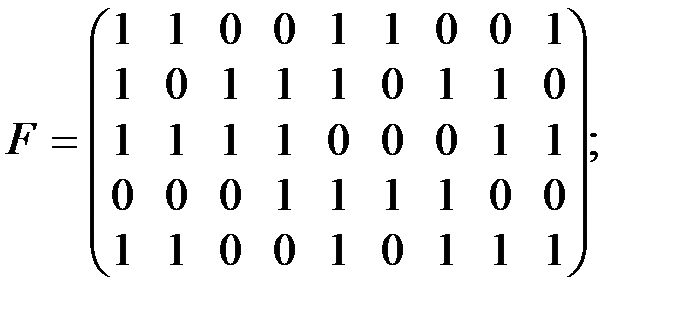а) б)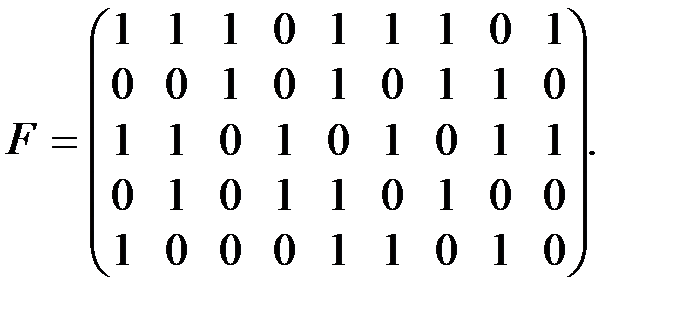

Задание3. С помощью матрицы 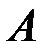закодировать информационное слово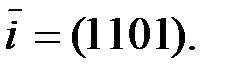

Решение. Кодовое слово из информационного получается с помощью порождающей матрицы по формуле 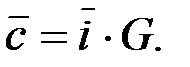В данном случае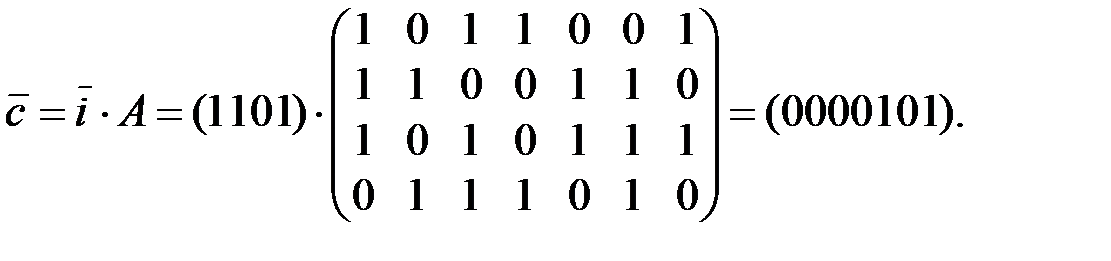

Задание4. С помощью матрицы 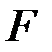закодировать информационное слово а) 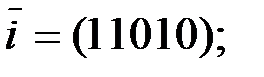б)

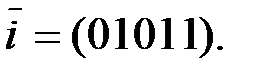
Задание5. В 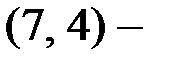коде 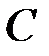с порождающей матрицей 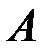однозначно ли восстанавливается информационное слово по данному кодовому слову ?

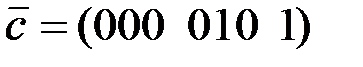Решение. Данное кодовое слово получено умножением неизвестного информационного слова 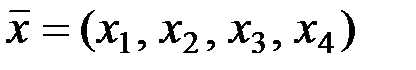на матрицу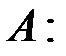 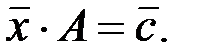Это равенство двух семимерных векторов. В координатной форме оно выглядит как система линейных алгебраических уравнений (СЛАУ) относительно неизвестных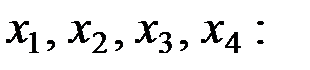

В процессе решения задания 1 мы установили, что один из базисных миноров матрицы 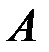расположен в 1-м, 2-м, 4-м и 5-м столбцах этой матрицы. Значит, полученная СЛАУ эквивалентна своей подсистеме из 1-го, 2-го, 4-го и 5-го уравнений. Выпишем эту подсистему в матричной форме: 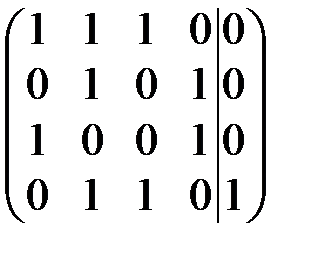. Несложные вычисления показывают, что данная подсистема, а с ней и вся система имеют единственное решение: 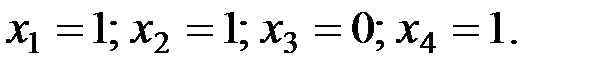Проведенные вычисления показывают, что существует единственный информационный вектор 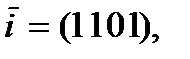порождающий данное кодовое слово .

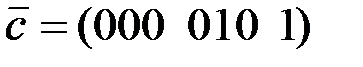Задание6. Убедиться, что полученные в задании 4 кодовые слова однозначно восстанавливаются до породивших их информационных слов.

Задание7. Попытайтесь «усовершенствовать» пример 1.1 проверкой на четность отдельно координат с нечетными номерами и отдельно – с четными номерами. Постройте проверочную матрицу нового кода.

1. Выяснить, может ли заданная матрица (по вариантам) быть порождающей матрицей линейного кода?

2. Закодировать с помощью матрицы из первого задания сообщение 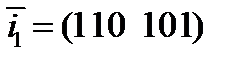для четных вариантов и задание 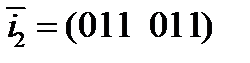для нечетных вариантов.

3. По полученному в задании 2 кодовому слову однозначно восстановить исходное информационное сообщение.

Вариант 1 Вариант 2

Вариант 3 Вариант 4

Вариант 5 Вариант 6

Вариант 7. Вариант 8

Вариант 9 Вариант 10

Вариант 11 Вариант 12

Вариант 13 Вариант 14

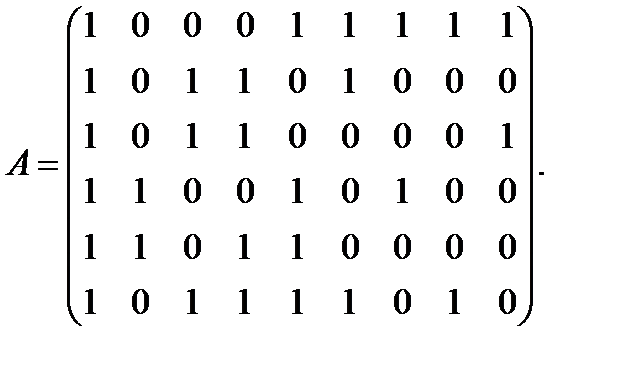
Вариант 15 Вариант 16

Практическое занятие №2

Дата добавления: 2017-02-01