
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лист контролю.
|
|
|
|
Модуль №6.
Координатами.
Нехай в системі координат ХОУ задані  і
і  . Тоді:
. Тоді:
1.  Координати суми (різниці) двох векторів дорівнює сумі (різниці) однойменних координат цих векторів.
Координати суми (різниці) двох векторів дорівнює сумі (різниці) однойменних координат цих векторів.
2.  При множенні вектора на число, на це число перемножують його координати.
При множенні вектора на число, на це число перемножують його координати.
3.  Скалярний добуток двох векторів дорівнює сумі добутків однойменних координат.
Скалярний добуток двох векторів дорівнює сумі добутків однойменних координат.
4.  Модуль вектора дорівнює кореневі квадратному із суми квадратів його координат.
Модуль вектора дорівнює кореневі квадратному із суми квадратів його координат.
5.  формула кута між двома векторами.
формула кута між двома векторами.
 умови колінеарності векторів. Заданих своїми векторами.
умови колінеарності векторів. Заданих своїми векторами.
9. Векторний добуток векторів.
Векторним добутком вектора  на не колінеарний вектор
на не колінеарний вектор  називається такий вектор
називається такий вектор  , який задовольняє наступні вимоги:
, який задовольняє наступні вимоги:
1. Вектор  перпендикулярний вектору
перпендикулярний вектору  і вектору
і вектору  , тобто площині, яка містить вектори
, тобто площині, яка містить вектори  і
і  ;
;
2. Довжина вектора  чисельно дорівнює площі паралелограма, побудованого на векторах
чисельно дорівнює площі паралелограма, побудованого на векторах  і
і  як на сторонах
як на сторонах  .
.
3. Орієнтація векторів  ,
,  ,
,  співпадає з орієнтацією векторів
співпадає з орієнтацією векторів
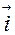 ,
,  ,
,  (права трійка).
(права трійка).
Властивості:
1.  ; 3.
; 3.  ;
;
2.  ; 4. Якщо
; 4. Якщо  то
то  .
.
Якщо  , то:
, то:
 формула векторного добутку
формула векторного добутку
векторів, заданих своїми координатами.
10. Відстань між двома точками. Ділення
відрізка в заданому відношенні і навпіл.
Якщо 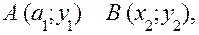 то
то 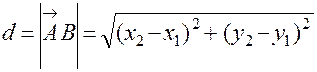 ,
,
або  Якщо
Якщо  і
і  , де
, де 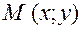 , то
, то 
 . Якщо точка М ділить відрізок АВ, то
. Якщо точка М ділить відрізок АВ, то 
 .
.
11. Пряма лінія на площині.
1. Рівняння  називається канонічним, або рівнянням прямої, що проходить через точку з заданим направляючим вектором.
називається канонічним, або рівнянням прямої, що проходить через точку з заданим направляючим вектором.
2. Рівняння  називається параметричним рівнянням прямої.
називається параметричним рівнянням прямої.
3.  рівняння прямої, що проходить через задану точку з заданим нормальним вектором.
рівняння прямої, що проходить через задану точку з заданим нормальним вектором.
4. Рівняння  в прямокутній системі координат визначає пряму і причому єдину (загальне рівняння прямої).
в прямокутній системі координат визначає пряму і причому єдину (загальне рівняння прямої).
5. Частинні випадки загального рівняння прямої: 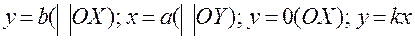 (через початок координат);
(через початок координат);  (з кутовим коефіцієнтом і початковою координатою).
(з кутовим коефіцієнтом і початковою координатою).
6. 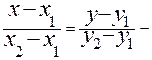 рівняння прямої, що проходить через дві точки.
рівняння прямої, що проходить через дві точки.
7.  рівняння прямої, що проходить через задану точку з заданим кутовим коефіцієнтом (рівняння пучка прямих).
рівняння прямої, що проходить через задану точку з заданим кутовим коефіцієнтом (рівняння пучка прямих).
8. 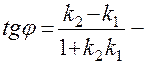 формула кута між двома перетинаючими прямими.
формула кута між двома перетинаючими прямими.
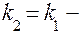 умова паралельності прямих,
умова паралельності прямих,
 умова перпендикулярності прямих.
умова перпендикулярності прямих.
12. Криві другого порядку.
1. Коло.
Множина всіх точок площини, однаково віддалених від даної точки (центра) називається колом.
 рівняння кола, з центром в точці
рівняння кола, з центром в точці  і радіусом R.
і радіусом R.

2. Еліпс.
Еліпсом називається множина всіх точок площини, сума відстаней від кожної із яких до двох заданих точок, які називаються фокусами, є величина постійна, більша, ніж відстань між фокусами.
 канонічне рівняння еліпса, 2а – велика вісь еліпса;
канонічне рівняння еліпса, 2а – велика вісь еліпса;  мала вісь еліпса; 2с – фокусна відстань;
мала вісь еліпса; 2с – фокусна відстань;  зв’язок між елементами а, b і с.
зв’язок між елементами а, b і с.  ексценрисітет еліпса.
ексценрисітет еліпса.

3. Гіпербола.
Гіперболою називається множина всіх точок площини, модуль різниці відстаней від кожної з яких до двох заданих точок, які називаються фокусами, є величина постійна, менша, ніж фокусна відстань.
 канонічне рівняння гіперболи, 2а – дійсна вісь;
канонічне рівняння гіперболи, 2а – дійсна вісь;
 уявна вісь;
уявна вісь;  рівняння асимптот;
рівняння асимптот;  зв’язок між елементами а, b і с. Якщо
зв’язок між елементами а, b і с. Якщо 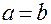 , то гіпербола називається рівносторонньою і її рівняння
, то гіпербола називається рівносторонньою і її рівняння  .
.

4. Парабола.
Параболою називається множина всіх точок площини, кожна з яких однаково віддалена від точки, яка називається фокусом і від прямої, яка називається директрисою.
 канонічне рівняння параболи, р – параметр параболи (це відстань від фокуса до директриси.)
канонічне рівняння параболи, р – параметр параболи (це відстань від фокуса до директриси.)

13. Рівняння прямої і площини в просторі.
1. Рівняння прямої в просторі.
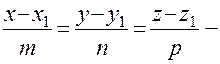 канонічне рівняння прямої в просторі, або рівняння прямої, що проходить через задану точку з заданим направляючим вектором.
канонічне рівняння прямої в просторі, або рівняння прямої, що проходить через задану точку з заданим направляючим вектором.

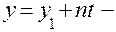 параметричне рівняння прямої.
параметричне рівняння прямої.

 рівняння прямої, що проходить через дві точки.
рівняння прямої, що проходить через дві точки.
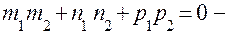 умова перпендикулярності прямих.
умова перпендикулярності прямих.
 умова паралельності прямих.
умова паралельності прямих.
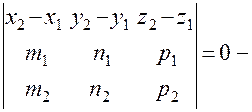 умова того, що прямі лежать в одній площині.
умова того, що прямі лежать в одній площині.
 Формула конуса кута між двома перетинаючи ми прямими.
Формула конуса кута між двома перетинаючи ми прямими.
1. Рівняння площини.
 рівняння площини, що проходить через задану точку з заданим нормальним вектором.
рівняння площини, що проходить через задану точку з заданим нормальним вектором.
Якщо в загальному рівнянні площини відсутній член з якою-небудь змінною, то площина паралельна відповідній вісі координат.
Якщо в загальному рівнянні площини два коефіцієнти при змінних дорівнюють нулю, то площина паралельна відповідній координатній площині.
 рівняння площини, що проходить через три точки.
рівняння площини, що проходить через три точки.
 умова паралельності площини.
умова паралельності площини.
 умова перпендикулярності площин.
умова перпендикулярності площин.
 формула косинуса кута між двома площинами.
формула косинуса кута між двома площинами.
 умова паралельності прямої і площини.
умова паралельності прямої і площини.
 формула синуса кута між прямою і площиною.
формула синуса кута між прямою і площиною.
1. Поняття вектора.
2. Лінійні операції над векторами.
3. Базис і координати. Прямокутні координати на площині та в просторі.
4. Координати вектора.
5. Дії над векторами в координатній формі.
6. Умова колінеарність векторів.
7. Скалярний добуток векторів.
8. Умова перпендикулярності векторів.
9. Кут між векторами.
10. Відстань між двома точками.
11. Ділення відрізка в заданому відношенні.
12. Векторний добуток векторів.
13. Пряма на площині і її рівняння. Загальне рівняння прямої і його дослідження. Канонічне рівняння прямої, нормальне рівняння прямої. Кут між прямими.
14. Криві другого порядку. Коло. Еліпс. Гіпербола. Парабола.
15. Рівняння прямої в просторі.
16. Рівняння площини, яка задана точкою і нормальним вектором.
Література:
1. О.М. Афанасьєва «Математика». 2001р.
2. О.М. Афанасьєва «Дидактичні матеріали з математики». 2001р.
3. О.В. Погорєлова «Геометрія». 10 – 11 кл. 1995р.
4. Н.Г. Федін «Геометрія». 1989р.
5. Н.В. Богомолов «Практические занятия по математике». 1990г.
Тема №7: Інтеграл та його застосування.
1. Неозначений інтеграл та його застосування.
2. Таблиця основних інтегралів.
3. Методи інтегрування.
4. Означений інтеграл.
5. Геометричний зміст означеного інтеграла.
6. Основні властивості означеного інтеграла.
7. Формула Ньютона – Лейбніца.
8. Застосування означеного інтеграла.
1. Неозначений інтеграл та його застосування.
Означення. Функція  , визначена на множині х називається первісною для
, визначена на множині х називається первісною для  , визначеною на цій же множині х, якщо для всіх х із цієї множини
, визначеною на цій же множині х, якщо для всіх х із цієї множини  , або
, або 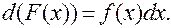
Теорема. Якщо функція  являється первісною для
являється первісною для  на деякій множині х, то функція
на деякій множині х, то функція 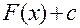 також являється первісною для
також являється первісною для  на множині х.
на множині х.
Означення. Сукупність первісних 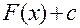 для
для  , означених на множині х називається неозначеним інтегралом від функції
, означених на множині х називається неозначеним інтегралом від функції  на множині х і позначається:
на множині х і позначається:

 підінтегральна функція.
підінтегральна функція.
 підінтегральний вираз.
підінтегральний вираз.
с – постійна інтегрування.
Властивості неозначеного інтеграла.
1. Похідна від неозначеного інтеграла дорівнює підінтегральній функції 
2. Диференціал від неозначеного інтеграла дорівнює підінтегральному виразу 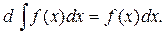
3. Постійний множник можна виносити за знак інтеграла 
4. Неозначений інтеграл від алгебраїчної суми двох неперервних функцій дорівнює алгебраїчній сумі інтегралів від кожної з цих функцій 
2. Таблиця основних інтегралів.
1.  14.
14. 
2.  15.
15. 
3.  16.
16. 
4. 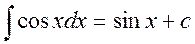 17.
17. 
5.  18.
18. 
6.  19.
19. 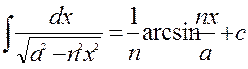
7.  20.
20. 
8. 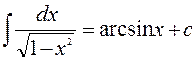 21.
21. 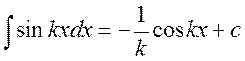
9.  22.
22. 
10.  23.
23. 
11.  24.
24. 
12.  25.
25. 
13. 
3. Методи інтегрування.
 метод підстановки.
метод підстановки.
 формула інтегрування за частинами.
формула інтегрування за частинами.
Визначений інтеграл.
Нехай  неперервна на
неперервна на  . Якщо існує границя послідовності інтегральних сум, одна і таж, незалежно від вибору точки
. Якщо існує границя послідовності інтегральних сум, одна і таж, незалежно від вибору точки 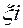 , то
, то  називається інтегральною, границя називається означеним інтегралом і позначається
називається інтегральною, границя називається означеним інтегралом і позначається 

а – нижня межа інтегрування;
b – верхня межа інтегрування;
 підінтегральна функція;
підінтегральна функція;
 підінтегральний вираз.
підінтегральний вираз.
Геометричний зміст визначеного інтеграла.
Якщо інтегрована на  функція
функція  невід’ємна, то означений інтеграл
невід’ємна, то означений інтеграл  чисельно дорівнює площі S криволінійної трапеції, обмеженої графіком функції
чисельно дорівнює площі S криволінійної трапеції, обмеженої графіком функції  , віссю ОХ і прямими х=а і х=b.
, віссю ОХ і прямими х=а і х=b.

Основні властивості визначеного інтеграла.
1. Постійний множник можна виносити за знак інтеграла  ;
;
2. Означений інтеграл від алгебраїчної суми двох неперервних функцій дорівнює алгебраїчній сумі їх інтегралів  ;
;
3. Якщо a < c < b, то 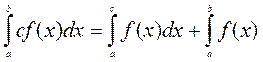 ;
;
4. Якщо функція  на
на  , де a < b, то
, де a < b, то  ;
;
5. Якщо  для
для  , то
, то  ;
;
Якщо т і М – найменше і найбільше значення функції  ;
;
6. на  , де a < b, то
, де a < b, то  ;
;
7. Теорема про середнє.
Якщо функція  неперервна на
неперервна на  , то існує точка
, то існує точка  така, що
така, що  ;
;
8. 
Формула Ньютона – Лейбніца.
Якщо функція  неперервна на проміжку
неперервна на проміжку  , а
, а  являється якою-небудь її первісною на цьому проміжку, то
являється якою-небудь її первісною на цьому проміжку, то 
Формула Ньютона – Лейбніца записується в вигляді:  і показує, що значення інтеграла дорівнює різниці значень первісної підінтегральної функції. Таким чином: щоб обчислити інтеграл
і показує, що значення інтеграла дорівнює різниці значень первісної підінтегральної функції. Таким чином: щоб обчислити інтеграл  , необхідно:
, необхідно:
1. Знайти неозначений інтеграл від функції  .
.
2. В отриманий вираз підставити замість х спочатку верхню межу b, потім нижню межу а, і з першого результату відняти другий.
8. Застосування визначеного інтегралу.
1. Обчислення площ плоских фігур. 
Обчислення об’ємів.
а)  за площею поперечного перерізу;
за площею поперечного перерізу;
2. б)  об’єм тіла, утвореного обертанням навколо вісі ОХ;
об’єм тіла, утвореного обертанням навколо вісі ОХ;
в)  об’єм тіла, утвореного обертанням навколо вісі OY;
об’єм тіла, утвореного обертанням навколо вісі OY;
3. Довжина дуги кривої  ;
;
4. Площа поверхні обертання  ;
;
5. Робота змінної сили  ;
;
6. Обчислення маси стержня змінної густини  ;
;
7. Обчислення статистичних моментів і центра мас плоскої кривої 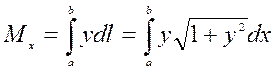

|
|
|
|
|
Дата добавления: 2017-02-01; Просмотров: 72; Нарушение авторских прав?; Мы поможем в написании вашей работы!