Точки перегину.

Графік функції , називається опуклим на , якщо графік розміщений нижче любої дотичної, проведеної до графіка функції в точках .

Графік функції , називається вгнутим на , якщо графік розміщений вище любої дотичної, проведеної до графіка функції в точках .

Достатня умова опуклості графіка функції:

Теорема. Якщо функція двічі диференційована на , і для , то графік функції вгнутий, якщо для , то графік функції опуклий.

Необхідна умова існування точка перегину.

Теорема. Якщо функція має неперервні похідні до другого порядку на і , являться точкою перегину, то .

Достатня умова.

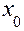Теорема. Якщо функція , , двічі диференційована на і при переході через друга похідна змінює знак, то точка кривої з абсцисою 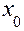являється точкою перегину.

Схема дослідження функції на перегин.

1. Знаходимо критичні точки другого роду.

2. Розміщуємо критичні точки в порядку зростання 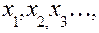підставляємо в другу похідну любе число менше , потім більше , але менше . Якщо при цьому друга похідна змінює знак, то при маємо точку перегину.

3. Обчислюємо 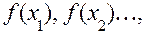тобто знаходимо перегин.

4. Друге правило дослідження на екстремум.

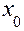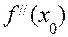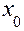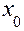Нехай точка є стаціонарною для функції і нехай в цій точці існує похідна другого порядку , яка не дорівнює нулю, . Тоді, якщо , то є точкою мінімуму, якщо , то є точкою максимуму функції .

5. Асимптоти кривої.

називається похилою асимптотою кривої при , якщо , Якщ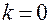о , то 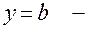горизонтальна асимптота, 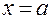називається вертикальною асимптотою, якщ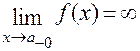о або .

6. Загальна схема дослідження функції та побудова графіка.

1. Знаходимо ;

2. Знаходимо точки перетину графіка функції з осями координат (якщо це можливо);

3. Досліджуємо на парність і непарність, парна, непарна;

4. Досліджуємо на монотонність та екстремум;

5. Досліджуємо на перегин;

6. Знаходимо асимптоти кривої;

7. Будуємо графік.

7. Рівняння дотичної до графіка функції в заданій точці.

Схема:

1. Знаходимо ;

2. Знаходимо ;

3. Складаємо рівняння,

8. Найбільше і найменше значення функції на відрізку.

Нехай функція неперервна на сегменті . Щоб знайти найбільше і найменше значення функції на сегменті , необхідно:

1. Знайти критичні точки першого роду;

Обчислити значення функції в критичних точках, які належать , і в кінцях сегменту. Вибрати серед цих значень найбільше та найменше значення функції.

Дата добавления: 2017-02-01