
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Сравнение исправленной выборочной дисперсии с гипотетической генеральной дисперсией нормальной совокупности
|
|
|
|
Задачи.
Сравнение дисперсий
4.1.1. Сравнение двух дисперсий нормальных генеральных
совокупностей
По независимым выборкам, объемы которых равны 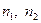 , извлеченным из нормальных генеральных совокупностей, найдены исправленные выборочные дисперсии
, извлеченным из нормальных генеральных совокупностей, найдены исправленные выборочные дисперсии  . Требуется сравнить эти дисперсии.
. Требуется сравнить эти дисперсии.
Правило 1. Для того, чтобы при заданном уровне значимости 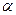 проверить нулевую гипотезу
проверить нулевую гипотезу 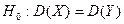 о равенстве генеральных дисперсий нормальных совокупностей при конкурирующей гипотезе
о равенстве генеральных дисперсий нормальных совокупностей при конкурирующей гипотезе  нужно вычислить наблюдаемое значение критерия (отношение большей исправленной дисперсии к меньшей)
нужно вычислить наблюдаемое значение критерия (отношение большей исправленной дисперсии к меньшей)

и по таблице критических точек распределения Фишера, по заданному уровню значимости 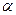 и числам степеней свободы
и числам степеней свободы 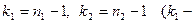 число степеней свободы, соответствующее выборке с большей исправленной дисперсией) найти критическую точку
число степеней свободы, соответствующее выборке с большей исправленной дисперсией) найти критическую точку  Если
Если  , то нет оснований отвергать нулевую гипотезу. В противном случае – ее отвергают.
, то нет оснований отвергать нулевую гипотезу. В противном случае – ее отвергают.
Правило 2. При конкурирующей гипотезе  критическую точку ищут по уровню значимости
критическую точку ищут по уровню значимости  , т.е.
, т.е.  Все остальное, как и в предыдущем случае.
Все остальное, как и в предыдущем случае.
1. По двум независимым выборкам объемов  извлеченным из нормальных генеральных совокупностей X и Y, найдены исправленные выборочные дисперсии
извлеченным из нормальных генеральных совокупностей X и Y, найдены исправленные выборочные дисперсии
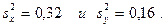
При уровне значимости  проверить нулевую гипотезу о равенстве генеральных дисперсий
проверить нулевую гипотезу о равенстве генеральных дисперсий 
при конкурирующей гипотезе

2. По двум независимым выборкам объемов  извлеченным из нормальных генеральных совокупностей X и Y, найдены исправленные выборочные дисперсии
извлеченным из нормальных генеральных совокупностей X и Y, найдены исправленные выборочные дисперсии

При уровне значимости  проверить нулевую гипотезу о равенстве генеральных дисперсий
проверить нулевую гипотезу о равенстве генеральных дисперсий 
при конкурирующей гипотезе

3. По двум независимым выборкам объемов  извлеченным из нормальных генеральных совокупностей X и Y, найдены исправленные выборочные дисперсии
извлеченным из нормальных генеральных совокупностей X и Y, найдены исправленные выборочные дисперсии

При уровне значимости  проверить нулевую гипотезу о равенстве генеральных дисперсий
проверить нулевую гипотезу о равенстве генеральных дисперсий 
при конкурирующей гипотезе

4. По двум независимым выборкам объемов  извлеченным из нормальных генеральных совокупностей X и Y, найдены выборочные дисперсии
извлеченным из нормальных генеральных совокупностей X и Y, найдены выборочные дисперсии

При уровне значимости  проверить нулевую гипотезу о равенстве генеральных дисперсий
проверить нулевую гипотезу о равенстве генеральных дисперсий 
при конкурирующей гипотезе

5. Двумя методами проведены измерения одного и того же экономического параметра. Получены следующие результаты
а) в первом случае 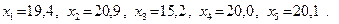
б) во втором случае 
Можно ли утверждать, что оба метода обеспечивают одинаковую точность измерений, если принять уровень значимости 0,1. Предполагается, что результаты измерений распределены нормально и выборки независимы.
6. Для сравнения точности двух станков-автоматов взяты 2 пробы (выборки) объемов  В результате измерения контролируемого размера отобранных изделий получены следующие результаты
В результате измерения контролируемого размера отобранных изделий получены следующие результаты

| 8,77 | 8,93 | 9,09 | 9,26 | 9,34 | 10,15 | 11,04 | 11,21 | 11,37 | 11,53 |

| 8,44 | 8,51 | 8,97 | 9,27 | 10,11 | 10,26 | 10,34 | 10,49 |
Можно ли считать, что станки обладают одинаковой точностью
 ,
,
если принять уровень значимости  и в качестве конкурирующей гипотезы принять
и в качестве конкурирующей гипотезы принять 
7. По двум независимым выборкам объемов  найдены исправленные выборочные дисперсии
найдены исправленные выборочные дисперсии

При уровне значимости  проверить нулевую гипотезу о равенстве генеральных дисперсий
проверить нулевую гипотезу о равенстве генеральных дисперсий 
8. По двум независимым выборкам, объемы которых  извлеченным из нормальных генеральных совокупностей X и Y, найдены исправленные выборочные дисперсии
извлеченным из нормальных генеральных совокупностей X и Y, найдены исправленные выборочные дисперсии 
При уровне значимости  проверить нулевую гипотезу о равенстве генеральных дисперсий при конкурирующей гипотезе:
проверить нулевую гипотезу о равенстве генеральных дисперсий при конкурирующей гипотезе: 
9. Расходы сырья 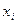 и
и  на единицу продукции по старой и новой технологиям приведены в таблице:
на единицу продукции по старой и новой технологиям приведены в таблице:
По старой технологии По новой технологии
| Расход сырья | 
| 
| |||||||
| Число изделий | 
| 
|
Предполагается, что генеральные совокупности 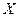 и
и  имеют нормальное распределения. Проверить гипотезу
имеют нормальное распределения. Проверить гипотезу  о равенстве дисперсий на уровне значимости
о равенстве дисперсий на уровне значимости  .
.
Обозначим через  объем выборки, по которой найдена исправленная дисперсия
объем выборки, по которой найдена исправленная дисперсия  .
.
Правило 1. Для того, чтобы при заданном уровне значимости 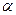 проверить нулевую гипотезу
проверить нулевую гипотезу 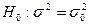 о равенстве неизвестной генеральной дисперсии
о равенстве неизвестной генеральной дисперсии  гипотетическому значению
гипотетическому значению  при конкурирующей гипотезе
при конкурирующей гипотезе  нужно вычислить наблюдаемое значение критерия
нужно вычислить наблюдаемое значение критерия 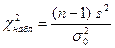
и по таблице критических точек распределения  , по заданному уровню значимости
, по заданному уровню значимости 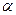 и числу степеней свободы
и числу степеней свободы  найти критическую точку
найти критическую точку 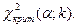 Если
Если  , то нет оснований отвергать нулевую гипотезу, в противном случае – ее отвергают.
, то нет оснований отвергать нулевую гипотезу, в противном случае – ее отвергают.
Правило 2. При конкурирующей гипотезе
 находят левую
находят левую  и правую
и правую  критические точки.
критические точки.
Если  , то нет оснований отвергать
, то нет оснований отвергать
нулевую гипотезу. В противном случае нулевую гипотезу отвергают.
Правило 3. При конкурирующей гипотезе
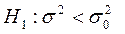 находят критическую точку
находят критическую точку  .
.
Если 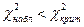 , то нет оснований отвергать нулевую гипотезу. В противном случае нулевую гипотезу отвергают.
, то нет оснований отвергать нулевую гипотезу. В противном случае нулевую гипотезу отвергают.
Замечание: Если число степеней свободы 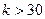 , то критическую точку
, то критическую точку 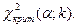 можно найти из равенства Уилсона-Гильферти
можно найти из равенства Уилсона-Гильферти
 , где
, где 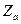 находят, используя функцию Лапласа из равенства
находят, используя функцию Лапласа из равенства  .
.
|
|
|
|
|
Дата добавления: 2017-02-01; Просмотров: 115; Нарушение авторских прав?; Мы поможем в написании вашей работы!