Сравнение выборочной средней с гипотетической генеральной средней нормальной совокупности

Задачи.

Задачи.

1. По выборке объема найден средний вес изделий, изготовленных на первом станке:

По выборке объема найден средний вес изделий, изготовленных на втором станке:

Генеральные дисперсии равны:

Требуется при уровне значимости 0,05 проверить нулевую гипотезу

При конкурирующей гипотезе:

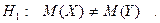
Предполагается, что X и Y распределены нормально и выборки независимы.

2. По двум независимым выборкам, объемы которых равны и 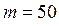, найдены выборочные средние

Генеральные дисперсии известны

При уровне значимости 0,01 проверить нулевую гипотезу

при конкурирующей гипотезе:

4.2.2. Сравнение двух средних нормальных генеральных совокупностей, дисперсии которых неизвестны и одинаковы (малые независимые
выборки.

Обозначим через и объемы малых независимых выборок, по которым найдены соответствующие выборочные средние и и исправленные выборочные дисперсии . Генеральные дисперсии хотя и неизвестны, но предполагаются одинаковыми.

Правило 1. Для того, чтобы при заданном уровне значимости проверить нулевую гипотезу о равенстве математических ожиданий (генеральных средних) двух нормальных генеральных совокупностей с неизвестными, но одинаковыми дисперсиями (в случае малых независимых выборок) при конкурирующей гипотезе

,

нужно вычислить наблюдаемое значение критерия

и по таблице критических точек распределения Стьюдента, по заданному уровню значимости, помещенному в верхней строке таблицы и числу степеней свободы 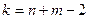найти критическую точку .

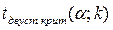Если - нет оснований отвергать нулевую гипотезу. В противном случае нулевую гипотезу отвергают.

Правило 2. При конкурирующей гипотезе

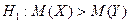
находят критическую точку по таблице по уровню значимости, помещенному в нижней строке таблицы, и тому же числу степеней свободы, что и в предыдущем случае ().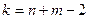

Если - нет оснований отвергать нулевую гипотезу. В противном случае нулевую гипотезу отвергают.

Правило 3. При конкурирующей гипотезе

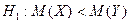
находят сначала критическую точку по правилу 2 и полагают

Если - нет оснований отвергать нулевую гипотезу. В противном случае нулевую гипотезу отвергают.

3. По двум независимым малым выборкам

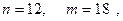
извлеченным из нормальных генеральных совокупностей X и Y, найдены выборочные средние

и исправленные дисперсии

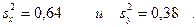
Требуется при уровне значимости 0,05 проверить нулевую гипотезу при конкурирующей гипотезе:

4. При уровне значимости 0,05 требуется проверить нулевую гипотезу при конкурирующей гипотезе

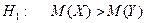
по малым независимым выборкам объемов

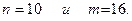
Получены следующие результаты

	14,1	14,3	14,6	15,0	15,4

	14,0	14,1	14,8

Указание: Предварительно проверить нулевую гипотезу при конкурирующей .

5. В цехе работают две линии по выпуску тротуарной плитки. Извлечены случайные выборки, с линии А 8 шт, а с линии В – 6. Результаты измерений толщины приведены в таблице:

А	7,0	7,1	7,3	7,2	7,6	7,7	7,4	7,5
В	7,7	7,2	7,5	7,4	7,5	7,9	-	-

Предполагая, что средние квадратические отклонения для этих линий равны, необходимо проверить гипотезу при альтернативности . Уровень значимости критерия примем равным 0,05.

6. Расходы сырья 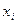и на единицу продукции по старой и новой технологиям приведены в таблице:

По старой технологии По новой технологии

Расход сырья
Число изделий

Предполагается, что генеральные совокупност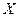и и имеют нормальное распределение с одинаковыми дисперсиями и средними . Требуется проверить гипотезу при конкурирующей при уровне значимости .

Дисперсия генеральной совокупности известна.

Правило 1. Для того, чтобы при заданном уровне значимости 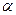проверить нулевую гипотезу

о равенстве генеральной средней нормальной совокупности с известной дисперсией гипотетическому (предполагаемому) значению при конкурирующей гипотезе

нужно вычислить наблюдаемое значение критерия

и по таблице функции Лапласа найти критическую точку 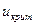двусторонней критической области из равенства

.

Если - то нет оснований отвергать нулевую гипотезу. В противном случае нулевую гипотезу отвергают.

Правило 2. При конкурирующей гипотезе критическую точку правосторонней критической области находят из равенства

Если - то нет оснований отвергать нулевую гипотезу. В противном случае нулевую гипотезу отвергают.

Правило 3. При конкурирующей гипотезе сначала находят вспомогательную критическую точку 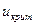по правилу 2, а затем полагают границу левосторонней критической области .

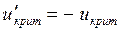Если - то нет оснований отвергать нулевую гипотезу. В противном случае нулевую гипотезу отвергают.

Дата добавления: 2017-02-01