Краткие теоретические сведения.

Марковский случайный процесс называется цепью Маркова с непрерывным временем, если переходы системы из состояния в состояние происходят не в фиксированные, а в случайные моменты времени. Время наступления событий часто предсказать заранее невозможно.

Условие нормировки , где вероятность того, что в момент времени 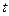система будет находиться в состоянии .

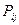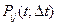Для процесса с непрерывным временем вместо переходных вероятностей используются плотности вероятностей перехода , где - вероятность того, что система, пребывавшая в момент времени t в состоянии , за время перейдет в состояние .

1. Уравнение Колмогорова

Уравнение Колмогорова составляют по размеченному графу состояний системы, пользуясь правилом: производная вероятности каждого состояния равна сумме всех потоков вероятности, идущих из других состояний в данное состояние, минус сумма всех потоков вероятности, идущих из данного состояния в другие.

Для решения системы уравнений Колмогорова необходимо задать начальное распределение вероятностей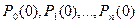

2. Финальные вероятности состояний системы.

Если процесс, протекающий в системе, длится достаточно долго, то имеет смысл говорить о предельном (финальном) поведении вероятностей при , т.е.

,

Говорят, что в системе устанавливается предельный стационарный режим, при котором она переходит из состояния в состояние, но вероятности состояний 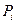уже не меняются во времени.

Финальные вероятности системы получаются путем решения системы линейных алгебраических уравнений, которые получаются из дифференциальных уравнений Колмогорова, если приравнять производные к нулю, а вероятности функции состояний в правых частях уравнений заменить на неизвестные финальные вероятности 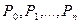. Для нахождения их точных значений к уравнениям добавляют нормировочное уравнение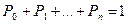

Получаемые в результате предельные вероятности представляют собой среднее относительное время пребывания системы в каждом из состояний.

Дата добавления: 2017-02-01