Сравнение дисперсий.

Двумерные случайные величины.

Нормальное распределение и его свойства.

Важнейшие распределения.

Бернулли.

Схема Бернулли. Предельные теоремы для схемы

Формула полной вероятности и формула Байеса.

Формулы сложения и умножения вероятностей.

1. 0,875; 0,833; 0,875; 2. 0,055; 3. 0,585; 4. 0,991; 5. 0,292; 6. 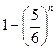; 7.а) 0,539;

б) 0,00036; в) 0,38; г) 0,461; 8. 0,727; 9. 0,92; 10. 0,115; 13. 0,18; 14. 0,384; 15. 0,002;

16. 0,35; 17. 0,88; 18. 0,675; 19. 0,6; 20.а) 0,03; б) 0,03; в) 0,97; 21. 0,02; 22. 0,28; 23.а) 0,375; б) 0,625; 24. 0,44; 25. 0,033; 26. 0,72; 27. 0,7; 28. 0,667; 29. 0,63; 30. 0,238; 32. 0,96;

1. 0, 002167; 2. 0,44; 3. 0,53; 4. 0,038; 5. 0,545; 6. 0,16; 7. 0,808; 8. 0,34; 9. 0,922; 10. вероятность одинаковая; 11. 0,915; 12.а) 0,952; б) 0,048; 13. 0,143; 14. 0,946; 15.а) 0,41; б) 0,652; 16. 0,00725; 17. 0,361; 18. 0,227; 19. 0,042; 20. 0,725; 21.а) 0,033; б) 0,36; 22. 0,3; 23. 0,19; 24. 0,6; 25. 0,84; 26. 0,575; 27. 0,429; 28. 0,978; 29.а) 0,136; б) 0,111; 30. 0,96; 31. 0,852; 32. 0,0025; 33. 0,9962; 34. 0,8554;

1.а) 0,43; б) 0,149; 2.а) 0,383; б) 0,853; 3. 0,055; 4. 0,528; 5. 7; 6.а) 0,007; б) 1; в) 0,41; 7. 0,902; 8. 0,345; 9.а) 0,347; б) 0,057; 11. от191 до 197; 12. ; 14. 7 и 8; 15.а) 0,006; б) 0,398; в) 0,092; г) 0,504; 16.а) 0,581; б) 0,07; в) 0,994; 17. 0,101;
18.а) 0,151; б) 0,983; 19.а) 0,168; б) 0,423; 20.а) 0,161; б) 0,998; 21. 0,012; 22. 0,02; 23. 100; 24.а) 0,0207; б) 0,2435; 25. 0,511; 26. а) 0,3487; б) 0,0574; в) 0,9872; 27.а) 0,348; б) 0,239;

в) 0,109; г) 0,254; 28. 0,3; 29. 0,914; 30. 17; 31. 0,046; 32. 0,974; 33. 23; 34.а) 0,25; б) 0,75; 35. 0,466; 36.а) 0,3024; б) 0,4404; 0,2114; 0,0404; 0,0024; в) 0,6976; г) 0,2572; 37.а) 0,498;

б) 0,777; в) 0,982; 38. 0,441; 39. 0,5; 40. 5 и p=0,1793; 41. 0,1639; 42. 0,197; 0,345; 0,262; 0,000064; 43.а) ; б) 0,126; 44.а) 0,246; б) 0,669; 46. 0,193; 47. 0,9965;

Глава 2.

2.1 Законы и функции распределения случайных
величин.

1. 4. 0,6; 5. 0,366; 7. 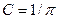; 0,7048; 8. 0,1875;

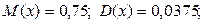
9. 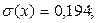10. 11. 1/9;

12.а) 281,25; б) 6,319; 16. 0,29; 17. 18.а) 0,5; в) 0; г) 0,354;

19. 20. 21. 62; 22. 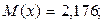23.а) 0,5; в) 0,875;

1.а) 4; б) 0,433; 2. 3; 3. ; 4.а) 0,0025; б) 0,0175; 5.б)

в) 0,451; 6.а) 333,33; б) 0,3; 7. 0,95; 8. 10.а) 0,4065; б) 0,463; в) 0,593; 11. 140; 12. 1,11; 13. 0,4; 14. 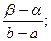15. 16. 0,368; 0,184; 0,0613; 0,0153; 18. 0,223; 19. 0,195; 20. 0,143; 21.а) 0,1563; б) 0,6289;

в) 0,7619; 22. 0,063; 23. 0,23; 24. 0,124; 25. 0,632; 26.а) 0,95; б) 0,199; в) 0,224; г) 0,577; 27.а) 0,091; б) 1; 28. 0,139; 29. 0,368; 30.а) 0,018; б) 0,865; в) 0,004; 31. 4;

1.а) 0,1587; б) 0,8413; в) 0,5007; 2. 10563; 3. 0,0078; 4. 37520; 5. 8,095; 7. 64;

8.в) 0,029; 9. М(х)=12; D(x)=16; 10.а) 0,159; б) 0,136; в) 0,683; 11.а) 0,1573; б) 0,1573;
12. (23,25;24,75); 13.а) (17,16;32,84); б) (20,84;29,16); 15. 0,125; 16. 0,866; 17. 0,1026;

18. 0,86; 19. 0,533; 20. 3; 21. 0,9973; 22. 0,3; 23.а) 0,8185; б) 0,9938; в) 0,1587; г) 0,9972; 24. 0,866; 25. 1,0156; 26. 27.а) 0,999; б) 0,776;

3. 0,8216; 4. 0,10355; 5. 0,0547; 9.б) 0,5625; 10.б) 0,67; 11.а) ; 12.б) ; в) 0,01049;

Глава 3.

3.1 Доверительные интервалы при известной
и неизвестной дисперсии

1.а) (8,13;15,87); б) (13,872;22,128); 2. (994,12;1005,88); 3.а) 0,0118; б) 0,0037;

4. 784; 5. 107; 6. (1176,48;1223,52); 7.( 1,099;3,1864); 8.а) ( 25,63;30,37); б) ( 24,5;31,5);
9. (-0,008;0,8582); 10. (37485;46515); 11. (767,13;832,87) и (115069,5;124930,53); 12. (2,16;5,84); 13.а) (0,0145;0,0855); б) (0;0,11);

14. 15. 0,206; 16. (74,72;121,68); 17. 0,99964.

Глава 4.

1. нет оснований отвергать ; 2. нет оснований отвергать ; 3. отвергается; 4. нет оснований отвергать ; 5. обеспе-чивают; 6. нет оснований отвергать ; 7. нет оснований отвергать ; 8. отвергается; 9. не отвергается; 10. нет оснований отвергать ; 11. нет оснований отвергать ; 12. отвергается; 13. не обеспечивает; 14. партию принять нельзя; 15. новичок работает неритмично; 16. не обеспечивает.

4.2 Сравнение средних генеральных совокупностей .

1. отвергается; 2. отвергается; 3. отвергается; 4. отвергается; 5. нет оснований отвергать ; 6. отвергается; 7.1) нет оснований отвергать ; 2) нет оснований отвергать ; 8. отвергается; 9.а) нет оснований отвергать ; б) отвергается; в) 167,49; 10) нет оснований отвергать ; 11. не обеспечивает; 12.а) нет оснований отвергать ; б) отвергается; 13. нет оснований отвергать ; 14. гипотеза о среднем размере дебиторского счета принимается; 15. по результатам выборки установлено соблюдение номинального размера.

Глава 5.

Дата добавления: 2017-02-01