Краткие теоретические сведения.

Цепи Маркова с дискретным временем

Задачи.

1. Найти коэффициент корреляции между величинами X и Y, совместный закон распределения которых задан следующей таблицей:

	0,2	0,02	0,01		0,23
	0,03	0,3	0,02		0,35
	0,02	0,1	0,2	0,1	0,42
	0,25	0,42	0,23	0,1

2. Двумерная случайная величина распределена по закону, приведенному в таблице:

Y X
-1	0,1	0,2
	0,2	0,3
		0,2

Определить коэффициент корреляции величин X и Y.

3. Двумерная случайная величина равномерно распределена в области D, ограниченной прямыми X=0, Y=0 и X+Y=4. Определить коэффициент корреляции величин X и Y.

4. Число Х выбирается случайным образом из множества (1,2,3). Затем из того же множества выбирается наудачу число Y, равное или большее Х. Найти коэффициент корреляции.

Глава 6. Цепи Маркова

1. Цепи Маркова представляют собой частный вид случайных процессов. Случайный процесс называется марковским, если для любого момента времени вероятность любого состояния системы в будущем зависит только от ее состояния в настоящем и не зависит от того, когда и каким образом система пришла в это состояние.

Цепью Маркова с дискретным временем называют цепь, изменение состояний которой происходит в определенные фиксированные моменты времени.

Цепью Маркова с непрерывным временем называют цепь, изменение состояний которой происходит в любые случайные возможные моменты времени.

Переходной вероятностью называют условную вероятность того, что из состояния в итоге следующего испытания система перейдет в состояние .

Матрицей перехода системы называют матрицу, которая содержит все переходные вероятности этой системы:

,

где - вероятности перехода за один шаг.

Основные свойства матрицы перехода:

1) Элементы каждой строки матрицы представляют собой вероятности всех возможных переходов за один шаг из выбранного состояния, в том числе и вероятность отсутствия перехода.

2) Элементы столбцов задают вероятности всех переходов системы за один шаг в заданное состояние.

3) В каждой строке матрицы вероятности перехода из состояния в любое возможное состояние образуют полную группу, поэтому (сумма вероятностей строки = 1)

4) По главной диагонали матрицы перехода стоят вероятности 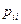того, что система не выйдет из состояния, а останется в нем.

2. Часто требуется при известных переходных вероятностях , найти вероятность перехода из состояния в состояние 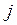за шагов.

Равенство Маркова через промежуточные шаги).

Как следствие из нее

3. Начальным распределением Марковской цепи называется распределение вероятностей состояний в начале процесса , где - вероятность нахождения системы в начальный момент времени в состоянии . В частности, если начальное состояние системы в точности известно, то начальная вероятность 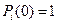, а все остальные равны нулю.

Если для однородной цепи Маркова заданы начальное распределение вероятностей и матрица перехода, то вероятности состояний системы на -ом шаге вычисляется

или

,

где () задает вероятности пребывания системы в состояниях после шагов, а задает начальное распределение вероятностей состояний системы, - матрица перехода.

4. Предельные вероятности состояний дискретной Марковской цепи определяются с помощью решения системы уравнений:

,

где - вектор-строка, компонентами которого являются предельные вероятности состояний, - матрица перехода, - единичная матрица, а второе соотношение учитывает условие нормировки.

Дата добавления: 2017-02-01