Лекция14. Поверхности второго порядка

Определение. Поверхностью второго порядка называется множество точек пространства координаты x, y которых, удовлетворяют уравнению

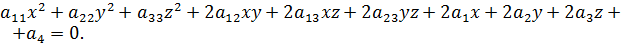(1)

. Сфера.

Если в уравнении (1) отсутствуют члены с произведением переменных, а коэффициенты при квадратах равны, то это всегда уравнение сферы, его можно привести к каноническому виду: (x - , где

С (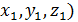 - центр сферы, а R – радиус.

Цилиндрические поверхности.

Определение. Поверхность, составленная из всех прямых, пересекающих данную линию L и параллельных данной прямой , называется цилиндрической поверхностью. При этом линия L – направляющая, а линия - образующая.

Рассмотрим в плоскости OXY некоторую линию L, имеющую в системе координат уравнение

F (x, y) = 0 (2)

Покажем, что это уравнение цилиндрической поверхности.

z Точка N – проекция точки М на плоскость XOY,

точка N лежит на L и удовлетворяет уравнению

(2). Точки M и N имеют одну и ту же абсциссу и

. M(x,y,z) ординату, и удовлетворяют уравнению (2), так

0 y как оно не содержит z. Координаты другой точки

не удовлетворяют уравнению (2). Таким обра-

x. N L -зом координаты любой точки цилиндрической

поверхности удовлетворяют уравнению (2), что

и хотели доказать.

Уравнение F(x, y)=0 является уравнением цилиндрической поверхности с образующими параллельными оси OZ и направляющей L, которая в плоскости OXY задаётся тем же уравнением F (x, y)=0. Аналогично, можно показать, что уравнение F (x, z)= 0 – уравнение цилиндрической поверхности с образующими параллельными оси OY, F (y,z) = 0 –уравнение цилиндрической поверхности с образующими параллельными оси OX. - эллиптический цилиндр с образующими параллельными

z оси OZ, если 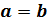, то круговой цилиндр.

0 y

2. - – гиперболический 3. – параболический ци-

цилиндр. –линдр, с образующими, парал-

лельными оси OX.

Z z

0 y 0 y

X x

. Конические поверхности.

Определение. Поверхность, составленная из всех прямых, пересекающих линию L и проходящих через данную точку Р, называется конической поверхностью. Линия L называется направляющей, точка Р - вершиной, а каждая из прямых, составляющих коническую поверхность – образующей.

Рассмотрим коническую поверхность с вершиной в начале координат и направляющей – эллипс.

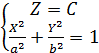(1) Это конус второго порядка.

Выберем произвольную точку М (x, y, z) и проведём образующую ОМ, пересекающую направляющую в точке N (X, Y, C). Уравнение прямой ОМ, прохо-

z дящей через две точки О (0,0,0) и

L. N N (X, Y, C) имеет вид:

. M 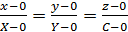или отсюда

0 y X = , Y = 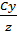эти значения подста-

x вим в (1).

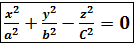→ Каноническое уравнение конуса 2-го порядка, симметричного относительно оси OZ.

Если 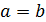, то 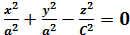→ прямой круговой конус.

Дата добавления: 2017-02-01