
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Отримання рівняння регресії
|
|
|
|
Лінійна модель парної регресії
Види рівнянь парної регресії й визначення параметрів
Парна регресія Множинна регресія
лінійна залежність
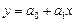
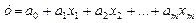 (1.1)
(1.1)
параболічна залежність

 (1.2)
(1.2)
гіперболічна залежність

 (1.3)
(1.3)
степенева залежність

 (1.4)
(1.4)
Рівняння (1.2)-(1.4) є нелінійними, але за допомогою перетворень їх можна звести до лінійної форми.
Лінійна регресія зводиться до знаходження рівняння виду

Побудова лінійної регресії зводиться до оцінки її параметрів –  і
і 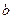 . Класичний підхід до оцінювання параметрів лінійної регресії заснований на методі найменших квадратів (МНК).
. Класичний підхід до оцінювання параметрів лінійної регресії заснований на методі найменших квадратів (МНК).
Система лінійних рівнянь для оцінки параметрів  і
і 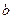 :
:
 (1.5)
(1.5)
Параметр 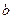 називається коефіцієнтом регресії. Його величина показує середню зміну результату
називається коефіцієнтом регресії. Його величина показує середню зміну результату 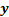 зі зміною фактору
зі зміною фактору 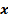 на одну одиницю. Можливість чіткої економічної інтерпретації коефіцієнта регресії зробила лінійне рівняння регресії досить розповсюдженим в економетричних дослідженнях.
на одну одиницю. Можливість чіткої економічної інтерпретації коефіцієнта регресії зробила лінійне рівняння регресії досить розповсюдженим в економетричних дослідженнях.
Знаючи коефіцієнт регресії можна обчислити коефіцієнт еластичності (відносний ефект впливу фактору на результат) - на скільки відсотків у середньому зміниться результат 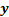 зі зміною фактору
зі зміною фактору 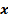 на 1%)
на 1%)
 . (1.6)
. (1.6)
Приклад 1. За даними проведеного опитування восьми груп родин відомі дані зв'язку витрат населення на продукти харчування з рівнем прибутків родини.
Витрати на продукти харчування, 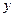 , тис. грн. , тис. грн.
| 0,9 | 1,2 | 1,8 | 2,2 | 2,6 | 2,9 | 3,3 | 3,8 |
Прибутки родини,
 , тис. грн. , тис. грн.
| 1,2 | 3,1 | 5,3 | 7,4 | 9,6 | 11,8 | 14,5 | 18,7 |
Припустимо, що зв'язок між прибутками родини й витратами на продукти харчування лінійний. Для підтвердження нашого припущення побудуємо поле кореляції.
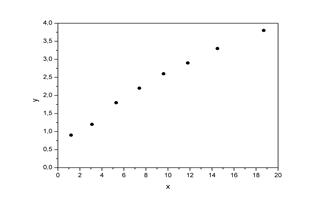
По малюнку видно, що точки вибудовуються в деяку пряму лінію.
Для зручності подальших обчислень складемо таблицю (заповнимо поки стовпці 1-4).
 
| 
| 
| 
| |
| 1,2 | 0,9 | 1,08 | 1,44 | |
| 3,1 | 1,2 | 3,72 | 9,61 | |
| 5,3 | 1,8 | 9,54 | 28,09 | |
| 7,4 | 2,2 | 16,28 | 54,76 | |
| 9,6 | 2,6 | 24,96 | 92,16 | |
| 11,8 | 2,9 | 34,22 | 139,24 | |
| 14,5 | 3,3 | 47,85 | 210,25 | |
| 18,7 | 3,8 | 71,06 | 349,69 | |
| Разом | 71,6 | 18,7 | 208,71 | 885,24 |
| Середнє значення | 8,95 | 2,34 | 26,09 | 110,66 |
Розрахуємо параметри лінійного рівняння парної регресії  . Для розв’язання системи (1.5) зручно подати цю систему за допомогою матричного апарату:
. Для розв’язання системи (1.5) зручно подати цю систему за допомогою матричного апарату: 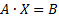 ,
,
де 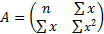 ,
, 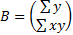 ,
,  .
.
Тоді коефіцієнти парної регресії визначаються за формулою:
 .
.
Одержали рівняння:  . (
. ( ,
, 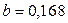 ). Такім чином, зі збільшенням прибутку родини на 1000 грн. витрати на харчування збільшуються на 168грн.
). Такім чином, зі збільшенням прибутку родини на 1000 грн. витрати на харчування збільшуються на 168грн.
Визначимо коефіцієнт еластичності (1.6) 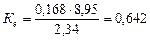 . На основі коефіцієнта еластичності можна зробити висновок, що зі збільшенням прибутків родини на 1% витрати на харчування збільшаться на 0,64%.
. На основі коефіцієнта еластичності можна зробити висновок, що зі збільшенням прибутків родини на 1% витрати на харчування збільшаться на 0,64%.
|
|
|
|
|
Дата добавления: 2017-02-01; Просмотров: 117; Нарушение авторских прав?; Мы поможем в написании вашей работы!