
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Оцінка тісноти й значимості зв'язку між змінними в рівняннях парної регресії.
|
|
|
|
Тісноту зв'язку оцінюють за допомогою таких характеристик: коефіцієнт кореляції й коефіцієнт детермінації.
Якщо зв'язок між показниками лінійний, то використовується лінійний коефіцієнт кореляції, що характеризує не тільки тісноту, але й напрямок.
Лінійний коефіцієнт кореляції  можна розрахувати як:
можна розрахувати як:
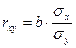 (1.7)
(1.7)
Оцінка щільності зв’язку здійснюється за такою шкалою:
 – зв'язок відсутній;
– зв'язок відсутній;
 – зв'язок слабкий;
– зв'язок слабкий;
 – зв'язок помірний;
– зв'язок помірний;
 – зв'язок помітний; (1.8)
– зв'язок помітний; (1.8)
 – зв’язок сильний;
– зв’язок сильний;
 – зв’язок достатньо сильний;
– зв’язок достатньо сильний;
 – зв’язок функціональний.
– зв’язок функціональний.
У випадку вже готового значення лінійного коефіцієнта кореляції, коефіцієнт детермінації розраховується як квадрат лінійного коефіцієнта кореляції 
 . Коефіцієнт детермінації показує, якою мірою варіація залежної змінної
. Коефіцієнт детермінації показує, якою мірою варіація залежної змінної 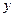 визначається варіацією незалежної змінної
визначається варіацією незалежної змінної  .
.
Коефіцієнт детермінації приймає значення від 0 (відсутній лінійний зв’язок між показниками) до 1 (відсутній кореляційний зв’язок між показниками).
Щоб мати загальне уявлення про якість моделі з відносних відхилень за кожним спостереженням, визначають середню помилку апроксимації:
 . (1.9)
. (1.9)
Середня помилка апроксимації не повинна перевищувати 8-10%.
Оцінка значимості рівняння регресії в цілому провадиться на основі  - критерію Фішера. Величина
- критерію Фішера. Величина  - критерію пов’язана з коефіцієнтом детермінації
- критерію пов’язана з коефіцієнтом детермінації  , і її можна розрахувати по наступній формулі:
, і її можна розрахувати по наступній формулі:
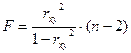 . (1.10)
. (1.10)
Фактичне значення  - критерію Фішера порівнюється з табличним значенням
- критерію Фішера порівнюється з табличним значенням 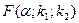 при рівні значимості
при рівні значимості  й степенях свободи
й степенях свободи  й
й 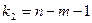 (для парної лінійної регресії
(для парної лінійної регресії  ). При цьому, якщо фактичне значення
). При цьому, якщо фактичне значення  - критерію більше за табличне, то визнається статистична значимість рівняння в цілому.
- критерію більше за табличне, то визнається статистична значимість рівняння в цілому.
У парній лінійній регресії оцінюється значимість не тільки рівняння в цілому, але й окремих його параметрів. Із цією метою по кожному з параметрів визначається його стандартна помилка:  і
і  .
.
Стандартна помилка коефіцієнта регресії визначається по формулі:
 ,
,
де 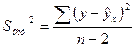 – залишкова дисперсія на одну степінь свободи.
– залишкова дисперсія на одну степінь свободи.
Величина стандартної помилки разом з  - розподілом Стьюдента при
- розподілом Стьюдента при  степенях свободи застосовується для перевірки істотності коефіцієнта регресії й для розрахунку його довірчого інтервалу.
степенях свободи застосовується для перевірки істотності коефіцієнта регресії й для розрахунку його довірчого інтервалу.
Для оцінки істотності коефіцієнта регресії його величина порівнюється з його стандартною помилкою, тобто визначається фактичне значення  - критерію Стьюдента:
- критерію Стьюдента: 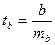 , яке потім порівнюється з табличним значенням при певному рівні значимості
, яке потім порівнюється з табличним значенням при певному рівні значимості  й числі степенів свободи
й числі степенів свободи  .
.
Довірчий інтервал для коефіцієнта регресії визначається як 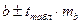 .
.
Стандартна помилка параметра  визначається по формулі:
визначається по формулі:

Процедура оцінювання істотності даного параметра не відрізняється від розглянутої вище для коефіцієнта регресії. Обчислюється  -критерій:
-критерій:  , його величина порівнюється з табличним значенням при
, його величина порівнюється з табличним значенням при  степенях свободи.
степенях свободи.
Довірчий інтервал для параметра 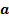 визначається як
визначається як  .
.
Значимість лінійного коефіцієнта кореляції перевіряється на основі величини помилки коефіцієнта кореляції  :
:
 .
.
Обчислюється  - критерій:
- критерій:  , його величина порівнюється з табличним значенням при
, його величина порівнюється з табличним значенням при  степенях свободи.
степенях свободи.
Розглянемо приклад 1 Одержали рівняння:  . Заповнимо стовпці 5-9.
. Заповнимо стовпці 5-9.
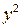
| 
| 
| 
|  , % , %
| |
| 0,81 | 1,038 | –0,138 | 0,0190 | 15,33 | |
| 1,44 | 1,357 | –0,157 | 0,0246 | 13,08 | |
| 3,24 | 1,726 | 0,074 | 0,0055 | 4,11 | |
| 4,84 | 2,079 | 0,121 | 0,0146 | 5,50 | |
| 6,76 | 2,449 | 0,151 | 0,0228 | 5,81 | |
| 8,41 | 2,818 | 0,082 | 0,0067 | 2,83 | |
| 10,89 | 3,272 | 0,028 | 0,0008 | 0,85 | |
| 14,44 | 3,978 | –0,178 | 0,0317 | 4,68 | |
| Разом | 50,83 | 18,717 | –0,017 | 0,1257 | 52,19 |
| Середнє значення | 6,35 | 2,34 | – | 0,0157 | 6,52 |

| – | – | – | – | – |
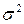
| – | – | – | – | – |
Як було зазначено вище, рівняння лінійної регресії завжди доповнюється показником тісноти зв'язку – лінійним коефіцієнтом кореляції  (1.7):
(1.7):
 .
.
Близькість коефіцієнта кореляції до 1 указує на те,що зв'язок між ознаками достатньо сильний.
Коефіцієнт детермінації  показує, що рівнянням регресії пояснюється 98,7% дисперсії результативної ознаки, а на частку інших факторів доводиться лише 1,3%.
показує, що рівнянням регресії пояснюється 98,7% дисперсії результативної ознаки, а на частку інших факторів доводиться лише 1,3%.
Оцінимо якість рівняння регресії в цілому за допомогою 
 - критерію Фішера. Обчислимо фактичне значення
- критерію Фішера. Обчислимо фактичне значення  - критерію (1.10):
- критерію (1.10):
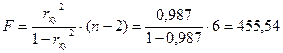 .
.
Табличне значення  .
.  , то визнається статистична значимість рівняння в цілому.
, то визнається статистична значимість рівняння в цілому.
Для оцінки статистичної значимості коефіцієнтів регресії й кореляції розрахуємо  - критерій Стьюдента й довірчі інтервали кожного з показників.
- критерій Стьюдента й довірчі інтервали кожного з показників.
Розрахуємо випадкові помилки параметрів лінійної регресії й коефіцієнта кореляції
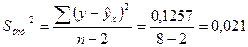



Фактичні значення  - статистик:
- статистик:
 ,
,  ,
, 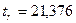 .
.
Табличне значення  критерію Стьюдента при
критерію Стьюдента при  й числі ступенів свободи
й числі ступенів свободи 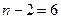 є
є  . Так як
. Так як  ,
, 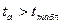 і
і  , то визнаємо статистичну значимість параметрів регресії й показника тісноти зв'язку.
, то визнаємо статистичну значимість параметрів регресії й показника тісноти зв'язку.
Розрахуємо довірчі інтервали для параметрів регресії  й
й 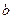 :
:  і
і 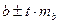 . Одержимо, що
. Одержимо, що 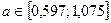 й
й  .
.
Середня помилка апроксимації (1.9) (знаходимо за допомогою стовпця 9)  говорить про високу якість рівняння регресії, тобто свідчить про добрий підбір моделі до вихідних даних.
говорить про високу якість рівняння регресії, тобто свідчить про добрий підбір моделі до вихідних даних.
|
|
|
|
|
Дата добавления: 2017-02-01; Просмотров: 185; Нарушение авторских прав?; Мы поможем в написании вашей работы!