
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Общее уравнение прямой на плоскости
|
|
|
|
Прямая на плоскости. Уравнение прямой с угловым коэффициентом. Общее уравнение прямой и его исследование
Определение 29.1: Под прямой линией будем понимать геометрическое место точек l такое, что для любых двух точек M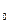 и M из данного множества вектор
и M из данного множества вектор 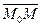 коллинеарен заданному ненулевому вектору
коллинеарен заданному ненулевому вектору 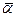 .
.
Или  .
.
Получим уравнение прямой линии на плоскости (то есть получим такое уравнение, которому должны удовлетворять координаты всех точек на прямой линии l и наоборот, если координаты некоторой точки удовлетворяют составленному уравнению, то эта точка лежит на прямой l).
Пусть и
и  (29.1)
(29.1)
Рассмотрим следующие случаи:
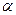 = 0. Тогда
= 0. Тогда  оси ординат OY, и первая координата x-x
оси ординат OY, и первая координата x-x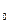 пропорциональна нулю, т.е.
пропорциональна нулю, т.е. (в этом случае
(в этом случае ) (29.2)
) (29.2)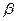 = 0. Тогда
= 0. Тогда 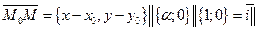 оси абсцисс OX, и вторая координата
оси абсцисс OX, и вторая координата 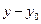 пропорциональна нулю, то есть
пропорциональна нулю, то есть 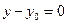 (в этом случае
(в этом случае  ) (29.3)
) (29.3)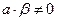 Так как
Так как  , то
, то 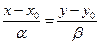 или
или 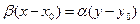 (29.4)
(29.4)
Раскрывая скобки и перенося все слагаемые в уравнении (29.4) в левую часть, получим.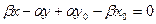 Положив
Положив 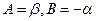 и
и 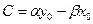 , из последнего уравнения имеем (при этом
, из последнего уравнения имеем (при этом  (см.(29.1)).
(см.(29.1)).
 (29.5)
(29.5)
и 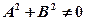 (29.6)
(29.6)
Отметим, что уравнения (29.2) (при A=1, B=0, C = ) и (29.3) (тогда A=0, B=1, C=
) и (29.3) (тогда A=0, B=1, C= ) является частичными случаями уравнения (29.5) с условием (29.6). Итак, мы показали, что если точка M принадлежит некоторой прямой l, то её координаты удовлетворяют некоторому уравнению (29.5) с условием (29.6) на коэффициенты A и B.
) является частичными случаями уравнения (29.5) с условием (29.6). Итак, мы показали, что если точка M принадлежит некоторой прямой l, то её координаты удовлетворяют некоторому уравнению (29.5) с условием (29.6) на коэффициенты A и B.
Покажем обратное, то есть если координаты всех точек M удовлетворяющих некоторому уравнению (29.5) с условием (29.6), то эти точки лежат на некоторой прямой l (удовлетворяющей определению 29.1).
ЗАДАЧА. Доказать, что если векторы 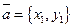 и
и 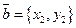 ортогональны некоторому вектору
ортогональны некоторому вектору 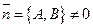 , то
, то 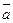 и
и  коллинеарные.
коллинеарные.
Для её решения заметим, что координаты векторов 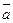 и
и  должны удовлетворять уравнению Ax+By=0, которое (см §17,18,19) является линейным пространством размерности 1 и, следовательно, всякие два решения этого уравнения линейно зависимы. Далее - §16.
должны удовлетворять уравнению Ax+By=0, которое (см §17,18,19) является линейным пространством размерности 1 и, следовательно, всякие два решения этого уравнения линейно зависимы. Далее - §16.
Заметим, что уравнение (29.5) имеет решения(например, если  (см.(29.6)), то координаты точек
(см.(29.6)), то координаты точек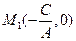 удовлетворяют уравнению (29.5).
удовлетворяют уравнению (29.5).
Пусть  и M(x,y) – любые решения уравнения (29.5), то есть:
и M(x,y) – любые решения уравнения (29.5), то есть:
 (29.5)
(29.5)
и 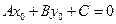 (29.7)
(29.7)
Вычитая из уравнения (29.5) уравнение (29.7), получим
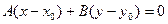 (29.8)
(29.8)
Это означает, что вектор 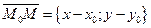 ортогонален вектору
ортогонален вектору 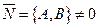 (см.(29.6)). Но и вектор
(см.(29.6)). Но и вектор 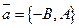 также ортогонален вектору
также ортогонален вектору  , потому что и скалярное произведение
, потому что и скалярное произведение  (см. §24). Поэтому
(см. §24). Поэтому  то есть точки
то есть точки 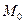 и М находятся на некоторой прямой линии l. Таким образом, уравнение (29.5) с условием (29.6) задает некоторую прямую линию l на плоскости
и М находятся на некоторой прямой линии l. Таким образом, уравнение (29.5) с условием (29.6) задает некоторую прямую линию l на плоскости  и наоборот, всякую линию l на плоскости
и наоборот, всякую линию l на плоскости  можно описать некоторым уравнением (29.5) с условием (29.6).
можно описать некоторым уравнением (29.5) с условием (29.6).
Определение 29.2: Уравнение (29.5) с условием (29.6) называется общим уравнением прямой линии на плоскости.
Определение 29.3: А вектор  называется нормальным вектором (или нормалью) к прямой l, заданной уравнением (29.5).
называется нормальным вектором (или нормалью) к прямой l, заданной уравнением (29.5).
Как уже было показано, вектор , то есть
, то есть 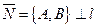
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 759; Нарушение авторских прав?; Мы поможем в написании вашей работы!