
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Случай общего уравнения прямых линий
|
|
|
|
| |||
 | |||
 Пусть прямые
Пусть прямые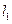 и
и 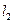 заданы уравнениями:
заданы уравнениями:
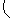
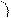

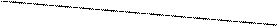

|
|
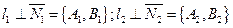
Тогда (см. чертеж 30.3) угол между прямыми 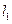 и
и 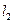 можно определить как угол между их нормалями
можно определить как угол между их нормалями 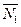 и
и 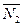 , и из §24 имеем:
, и из §24 имеем:
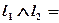
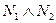
 (30.12)
(30.12)
Координаты точки пересечения прямых 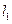 и
и 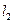 можно найти, решая систему из двух линейных уравнений (30.10) и (30.11). По формулам Крамера (см. §8) имеем:
можно найти, решая систему из двух линейных уравнений (30.10) и (30.11). По формулам Крамера (см. §8) имеем:
|
 x=
x= 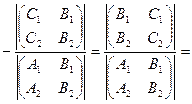
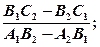
y= 
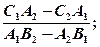
Для взаимного расположения прямых 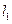 и
и 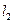 рассмотрим матрицы:
рассмотрим матрицы:

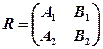 и
и 
(R - является матрицей системы линейных уравнений (30.10) и (30.11), а Q – её расширенной матрицей третий столбец которой, взят с противоположным знаком).
По теореме Кронекер-Капелли и критерию определенности системы (см. §13) имеем:
1.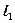 =
= 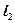
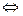
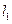 и
и 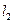 имеют бесконечно много точек пересечения, следовательно, система линейных уравнений (30.10) и (30.11) не определена
имеют бесконечно много точек пересечения, следовательно, система линейных уравнений (30.10) и (30.11) не определена  (30.14).
(30.14).
2. 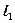 ||
|| 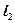
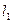 и
и  не имеют общих точек, следовательно, система линейных уравнений (30.10) и (30.11) не совместна
не имеют общих точек, следовательно, система линейных уравнений (30.10) и (30.11) не совместна 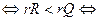
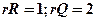 (30.15) (ввиду условия (29.6)
(30.15) (ввиду условия (29.6) 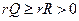 , а
, а 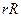 - ранг матрицы R).
- ранг матрицы R).
3. 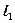 и
и 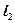 пересекаются в одной точке, следовательно, система линейных уравнений (30.10) и (30.11) определена
пересекаются в одной точке, следовательно, система линейных уравнений (30.10) и (30.11) определена 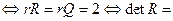
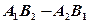 (30.16) и координаты их точки пересечения можно найти по формуле (30.13).
(30.16) и координаты их точки пересечения можно найти по формуле (30.13).
Условие перпендикулярности прямых 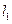 и
и 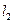 :
:
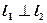
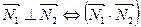 =
=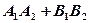 (30.14)
(30.14)
(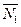 – нормаль к прямой
– нормаль к прямой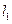 , а
, а 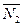 – нормаль к прямой
– нормаль к прямой 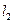 (см. чертёж 30.3))
(см. чертёж 30.3))
§31. Уравнение прямой на плоскости по двум точкам и «в отрезках»
31.1 Уравнение прямой проходящей через точку  и коллинеарной заданному вектору
и коллинеарной заданному вектору 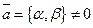
Данная прямая уже была получена в §29. Её уравнение имеет вид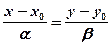 , или
, или 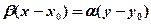 (см. уравнение (29.4))
(см. уравнение (29.4))
Второе равенство (29.4), в отличие от первого, допускает возможность 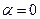 или
или 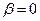 .
.
31.2 Уравнение прямой проходящей через заданную точку  и ортогональной заданному вектору
и ортогональной заданному вектору 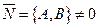
Эта прямая также была получена в §29, и её уравнение имеет вид:
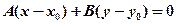 (см. уравнение (29.8)).
(см. уравнение (29.8)).
31.3 Уравнение прямой проходящей через две заданные точки 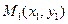 и
и 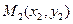
Это уравнение имеет вид:
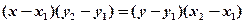 (31.1)
(31.1)
В случае 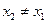 в (31.1) у можно выразить через x:
в (31.1) у можно выразить через x:
 (31.2)
(31.2)
А для 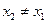 и
и 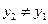 уравнение (31.1) можно записать следующим образом:
уравнение (31.1) можно записать следующим образом:
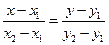
Читателю предполагаем самостоятельно получить уравнения (31.2) и (31.3) из (31.1), а также непосредственно проверить, что координаты точек 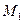 и
и  удовлетворяют
удовлетворяют
линейному уравнению (31.1), и поэтому прямая линия, задаётся уравнением (31.1), искомая (и единственная как прямая, проходящая через две заданные точки).
31.4 Уравнение прямой «в отрезках»
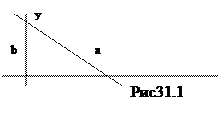 | |||
| |||
В §29 было показано, что всякую прямую, не параллельную ни одной из координатных осей и не проходящую через начало координат, можно записать уравнением
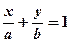 (29.9)
(29.9)
Подставив в уравнение (29.9) x=0, получим y=b, а из y=0 имеем x=a, то есть точки с координатами (a,0) и (0,b) находятся на прямой l (см. чертеж 31.1).Тогда 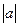 и
и 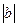 являются длинами отрезков, отсекаемых прямой l от координатного угла (числа a и b могут быть и отрицательными, из-за чего длины отрезков -
являются длинами отрезков, отсекаемых прямой l от координатного угла (числа a и b могут быть и отрицательными, из-за чего длины отрезков -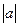 и
и 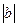 ).
).
Определение 31.1: Поэтому уравнение (29.9) называется уравнением прямой «в отрезках».
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 383; Нарушение авторских прав?; Мы поможем в написании вашей работы!
 l1
l1