Эллипс, как кривая второго порядка

Эллипс, как кривая второго порядка. Его полуоси, эксцентриситет, фокусы и директрисы. Окружность в качестве частного случая эллипса.

Определение 33.2. Эллипсом называется геометрическое место точек плоскости, для каждой из которых сумма расстояний до двух данных точек той же плоскости, называемых фокусами эллипса, есть величина постоянная.

Для эллипса можно дать еще несколько эквивалентных определений. Стоит отметить, что эллипс –– это кривая, получающаяся как проекция на плоскость π окружности, лежащей в плоскости, которая образует острый угол с плоскостью π.

В отличие от окружности, записать в "удобном" виде уравнение эллипса в произвольной системе координат крайне сложно. Поэтому для фиксированного эллипса приходится подбирать систему координат так, чтобы его уравнение было достаточно простым, т.е. получаем каноническое уравнение эллипса.

Пусть F₁ и F₂ –– фокусы эллипса. Начало O системы координат расположим на середине отрезка F₁F₂. Ось O_x направим вдоль этого отрезка, ось O_y –– перпендикулярно к этому отрезку (рис. 33.1).

Теорема 33.1. Пусть сумма расстояний от точки эллипса до фокусов равна 2a, а расстояние между фокусами –– 2c. Тогда в выбранной системе координат эллипс имеет уравнение

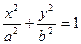
(33.2)

где

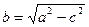
(33.5)

Доказательство. Пусть M (x; y) –– текущая точка эллипса. По определению эллипса F₁M + F₂M =2a. Из треугольника F₁MF₂ видно, что F₁M + F₂M > F₁F₂, то есть 2a > 2c, a > c, и поэтому число 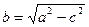существует (см. рис 33.1).

Рис. 33.1.

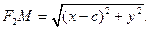Фокусами в выбранной системе координат являются точки F₁(-c; 0), F₂ (c; 0). Легко заметить, что

Тогда по определению эллипса

Перенесем один из корней вправо и обе части возведем в квадрат:

После того, как раскроем скобки и приведем подобные члены, приходим к выражению

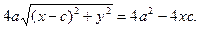
Разделим обе части этого уравнения на 4 и возведем в квадрат

Раскроем скобку и приведем подобные члены

Учитывая, что 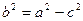(33.5), имеем равенство

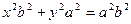
Наконец, разделив обе части на 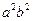, получим уравнение

(33.4)

Определение 33.3. Уравнение (33.4) называется каноническим уравнением эллипса.

Дата добавления: 2014-01-04