Расстояние от точки до прямой на плоскости

Для этого проведём прямую , проходящую через заданную точку и перпендикулярную заданной прямой 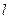. Пусть - точка пересечения прямых 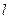и . Тогда расстояние от точки до прямой 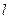совпадает с расстоянием между точками и 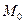(см. чертёж32.1).

Попутно мы решаем задачу получения уравнения прямой, проходящей через заданную точку и перпендикулярной заданной прямой.

Итак, пусть прямая задана уравнением (29.5) и – её нормаль .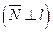

Тогда , то есть получается как прямая, проходящая через точку и коллинеарная вектору . Согласно §29 (см. равенство 29.4), её уравнение имеет вид 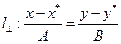или 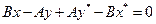(32.1)

Тогда - точка пересечения прямых, заданных уравнениями (29.5) и (32.1) и, по формулам (30.13) (для , и 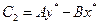), её координаты можно найти из уравнений:

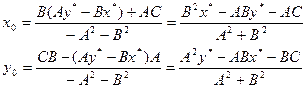(32.2)

	рис.32.1

Тогда расстояние:

=

=

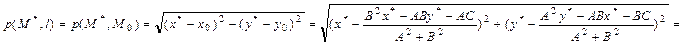
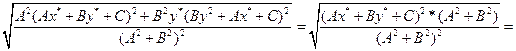
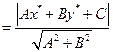
Итак, расстояние от точки M*(x*,y*) до прямой l, задаётся уравнением (29.5), можно найти по формуле:

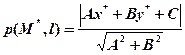(32.3)

ЗАДАЧА. Доказать, что координаты проекции точки M*(x*,y*) на прямую l, заданную уравнением (29.5), можно найти по формулам (32.2).

§§3335 Кривые второго порядка

Пусть на плоскости задана прямоугольная декартова система координат.

Определение 33.1. Линией второго порядка называется множество точек, координаты которых удовлетворяют уравнению второго порядка

ax^2 + bxy + cy^2 + dx +fy +g = 0

(33.1)

где a, b, c, d, f, g –– вещественные числа, и хотя бы одно из чисел a, b, c отлично от нуля.

Уравнение (33.1) в зависимости от коэффициентов может задавать только три типа кривых, а именно, эллипс (частным случаем которого является окружность), гиперболу и параболу. (Впрочем, могут быть также распадающиеся и вырожденные линии; более подробнее об этом в § 35).

Дата добавления: 2014-01-04