Определение f(A) в общем случае

Пусть m(x) – минимальный многочлен А и он имеет такое каноническое разложение 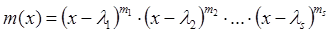, , 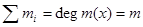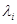– собственные значения А. Пусть многочлены g(x) и h(x) принимают одинаковые значения.

Пусть g(A)=h(A) (1), тогда многочлен d(x)=g(x)-h(x) – аннулирующий многочлен для А, так как d(A)=0, следовательно, d(x) делится на линейный многочлен, т.е. d(x)=m(x)*q(x) (2).

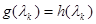Тогда , т.е. (3), , , .

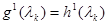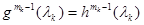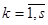Условимся m чисел для f(x) таких 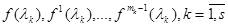называть значениями функции f(x) на спектре матрицы А, а множество этих значений будем обозначать .

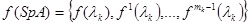Если множество f(Sp A) определено для f(x), то функция определена на спектре матрицы А.

Из (3) следует, что многочлены h(x) и g(x) имеют одинаковые значения на спектре матрицы А.

Наши рассуждения обратимы, т.е. из (3) Þ (3) Þ (1). Таким образом, если задана матрица А, то значение многочлена f(x) вполне определяется значениями этого многочлена на спектре матрицы А, т.е. все многочлены g_i(x), принимающие одинаковые значения на спектре матрицы имеют одинаковые матричные значения g_i(A). Потребуем, чтобы определение значения f(A) в общем случае подчинялось такому же принципу.

Значения функции f(x) на спектре матрицы А должны полносильно определить f(A), т.е. функции, имеющие одни и те же значения на спектре должны иметь одно и то же матричное значение f(A). Очевидно, что для определения f(A) в общем случае, достаточно найти многочлен g(x), который бы принимал те же значения на спектре А, что и функция f(A)=g(A).

Df. Если f(x) определена на спектре матрицы А, то f(A)=g(A), где g(A) – многочлен, принимающий на спектре те же значения, что и f(A),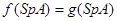

Df. Значением функции от матрицы А назовем значение многочлена от этой матрицы при .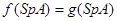

Среди многочленов из С[x], принимающих одинаковые значения на спектре матрицы А, что и f(x), степени не выше (m-1), принимающий одинаковые значения на спектре А, что и f(x) – это остаток от деления любого многочлена g(x), имеющего те же значения на спектре матрицы А, что и f(x), на минимальный многочлен m(x)=g(x)=m(x)*g(x)+r(x).

Этот многочлен r(x) называют интерполяционным многочленом Лагранжа-Сильвестра для функции f(x) на спектре матрицы А.

Замечание. Если минимальный многочлен m(x) матрицы А не имеет кратных корней, т.е. 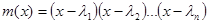, то значение функции на спектре .

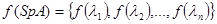Пример:

Найти r(x) для произвольной f(x), если матрица

. Построим f(H₁). Найдем минимальный многочлен H₁ – последний инвариантный множитель [xE-H₁]:

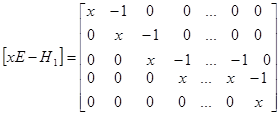, d_n-1=x²; d_n-1=1;

m_x=f_n(x)=d_n(x)/d_n-1(x)=xⁿÞ 0 – n –кратный корень m(x), т.е. n-кратные собственные значения H₁.

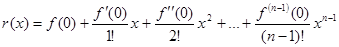, r(0)=f(0), r’(0)=f’(0),…,r^(n-1)(0)=f^(n-1)(0) Þ .

Дата добавления: 2014-01-04