КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Условный экстремум
|
|
|
|
Определение.Функция Rn®R имеет максимумв точке, если для всех из некоторой окрестности этой точки выполнено неравенство. Если неравенство строгое, то и максимум называется строгим. В случае неравенства говорят о точке минимума. И снова, если неравенство строгое, то − точка строгого минимума. Наконец, понятия максимума и минимума объединяет название экстремум.
Точки экстремума функций нескольких переменных.
Теорема 1. (Необходимое условие экстремума)В точке экстремума функции  каждая из её частных производных первого порядка равна нулю, либо не существует.
каждая из её частных производных первого порядка равна нулю, либо не существует.
Доказательство. Пусть, например, 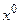 − точка максимума функции
− точка максимума функции  . В таком случае функция переменной
. В таком случае функция переменной 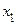
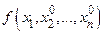 также имеет максимум
также имеет максимум 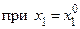 , следовательно, производная
, следовательно, производная 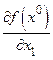 равна нулю или не существует. Это же относится и к другим частным производным первого порядка.
равна нулю или не существует. Это же относится и к другим частным производным первого порядка.
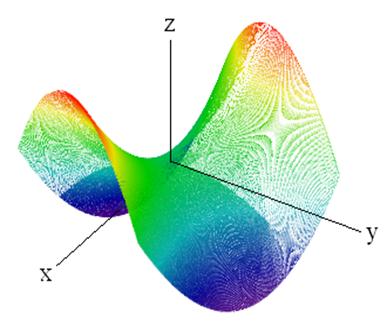
Замечание. Указанное необходимое условие экстремума не является достаточным. Это видно из простейших контрпримеров. Например, если 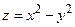 , то
, то 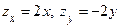 . Поэтому
. Поэтому 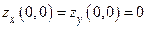 . В то же время, в любой окрестности точки
. В то же время, в любой окрестности точки  значение
значение 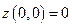 не является ни наибольшим, ни наименьшим. Действительно,
не является ни наибольшим, ни наименьшим. Действительно, 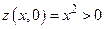 ,
, 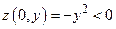 . (Это − так называемая седловая точка).
. (Это − так называемая седловая точка).
Теорема 2. (Достаточное условие наличия или отсутствия экстремума).
Пусть о функции 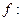 Rn®R класса
Rn®R класса 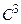 вблизи
вблизи 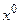 известно, что "
известно, что "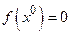 . В таком случае,
. В таком случае,
1) если 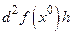 − положительно определенная квадратичная форма, т.е.
− положительно определенная квадратичная форма, т.е. 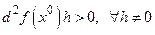 , то
, то 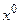 − точка минимума
− точка минимума  ;
;
2) если 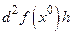 − отрицательно определенная квадратичная форма, т.е.
− отрицательно определенная квадратичная форма, т.е. 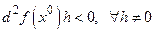 , то
, то 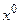 − точка максимума
− точка максимума  ;
;
3) если 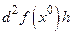 − знакопеременная квадратичная форма, т.е.
− знакопеременная квадратичная форма, т.е. 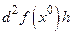 меняет знак, то в точке
меняет знак, то в точке 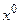 у данной функции нет экстремума;
у данной функции нет экстремума;
4) если 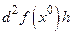 − полуопределённая квадратичная форма, т.е.
− полуопределённая квадратичная форма, т.е. 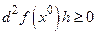 (либо
(либо 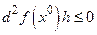 ), причем
), причем 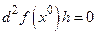 не только
не только 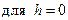 , то для получения ответа требуются дополнительные исследования (случай неопределённости).
, то для получения ответа требуются дополнительные исследования (случай неопределённости).
Доказательство. Как мы знаем, 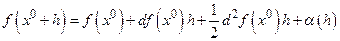 , где
, где
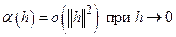 . Так как по условию "
. Так как по условию "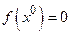 , то
, то 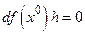 и
и
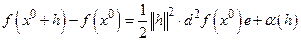 , где
, где 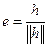 .
.
1) По теореме Вейерштрасса функция 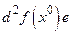 принимает на сфере
принимает на сфере 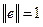 своё наименьшее значение
своё наименьшее значение 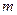 в некоторой точке
в некоторой точке 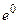 . Так как
. Так как 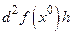 − положительно определенная форма и
− положительно определенная форма и 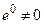 , то
, то 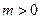 , поэтому
, поэтому 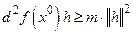 . С другой стороны, при достаточно малых значениях
. С другой стороны, при достаточно малых значениях 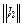 будет выполняться неравенство
будет выполняться неравенство 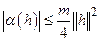 . Отсюда следует, что в окрестности точки
. Отсюда следует, что в окрестности точки 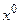 будем иметь
будем иметь
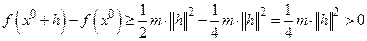 .
.
А это значит, что 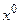 − точка минимума функции
− точка минимума функции  .
.
2) Для доказательства достаточно изменить знак 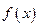 .
.
3) В этом случае существуют единичные векторы 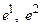 и число
и число 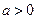 , для которых
, для которых 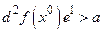 и
и 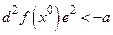 , Так как при достаточно малых значениях
, Так как при достаточно малых значениях 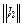 будет выполняться неравенство
будет выполняться неравенство 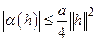 , то получим
, то получим
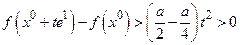 и
и 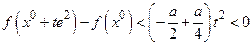
при малых положительных значениях 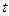 . Мы видим, что в точке
. Мы видим, что в точке 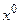 нет экстремума.
нет экстремума.
4) В этом случае, как показывают примеры, функция может иметь экстремум, а может и не иметь экстремума. (Рассмотреть функции 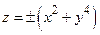 ,
, 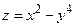 вблизи начала координат).
вблизи начала координат).
Для выяснения является ли квадратичная форма 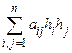 , где
, где 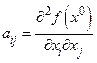 , положительно (отрицательно) определенной, можно использовать следующую теорему.
, положительно (отрицательно) определенной, можно использовать следующую теорему.
Критерий Сильвестра. Рассмотрим квадратичную форму 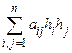 с матрицей коэффициентов A=
с матрицей коэффициентов A=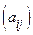 ,
, 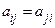 . Обозначим
. Обозначим 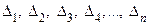 главные угловые миноры матрицы A. Для положительной определенности квадратичной формы необходимо и достаточно, чтобы знаки этих миноров были +, +, +, +,…,+; для ее отрицательной определенности необходимои достаточно, чтобы эти знаки были −, +, −, +,….
главные угловые миноры матрицы A. Для положительной определенности квадратичной формы необходимо и достаточно, чтобы знаки этих миноров были +, +, +, +,…,+; для ее отрицательной определенности необходимои достаточно, чтобы эти знаки были −, +, −, +,….
Частный случай: Пусть 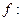 R2®R.
R2®R.
Обозначим 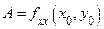 ,
, 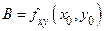 ,
, 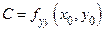 и
и 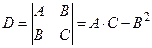 .
.
Если 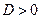 , то экстремум есть, именно:
, то экстремум есть, именно:
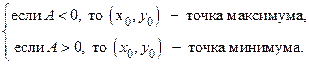
Если 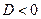 , то в точке
, то в точке 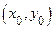 нет ни максимума, ни минимума.
нет ни максимума, ни минимума.
Если 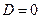 , то требуется дополнительное исследование.
, то требуется дополнительное исследование.
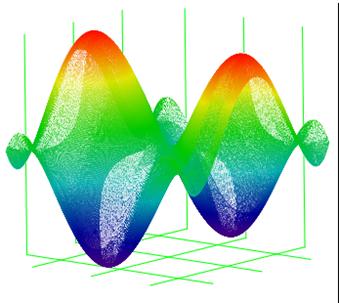
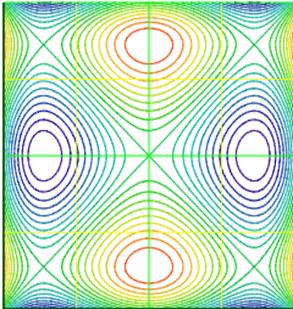
Пример. Исследовать на экстремум функцию 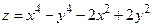 .
.
Решение. 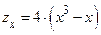 ,
, 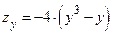 ;
;
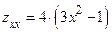 ,
, 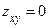 ,
, 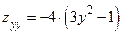 .
.
1) Используем необходимое условие экстремума для нахождения критических точек:
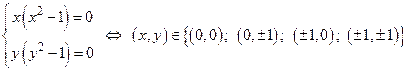 .
.
2) Применяем достаточные условия наличия или отсутствия экстремума. Результаты оформляем в виде таблицы.
| (0,0) | (0, ±1) | (±1,0) | (±1,±1) | Результат. | ||||
| A | -4 | -4 | Точки максимума: (0, ±1); zmax=1. Точки минимума: (±1, 0); zmin=−1. | |||||
| B | ||||||||
| C | -8 | -8 | ||||||
| D | -16 | -64 | ||||||
| нет | Макс. | Мин. | нет | |||||
| 
| |||||||
|
|
|
|
|
|
Дата добавления: 2013-12-13; Просмотров: 848; Нарушение авторских прав?; Мы поможем в написании вашей работы!