Решение. Наибольшее и наименьшее значение функции в замкнутой ограниченной области

Наибольшее и наименьшее значение функции в замкнутой ограниченной области.

Напомним. Для отыскания наибольшего (наименьшего) значения функции на отрезке мы добавляли к критическим точкам функции, лежащим внутри отрезка, его граничные точки. Затем сравнивали значения функции во всех указанных точках и отбирали наибольшее (наименьшее) из них.

В многомерном случае мы будем действовать по той же схеме. Только в этом случае граница области не сводится к двум концевым точкам. Найдя критические точки функции, лежащие внутри области, необходимо искать точки, подозрительные по условному экстремуму вдоль частей границы. У плоской области обычно части границы − это дуги границы и концы этих дуг. 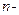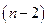В случае мерной области приходится иметь дело с -мерными, -мерными,...,1-мерными (дугами), наконец 0-мерными (точками) частями границы.

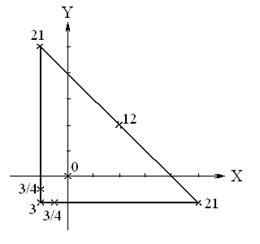
Пример 1. Найти наименьшее и наибольшее значения функции

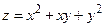
в замкнутой области .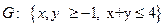

I. Критические точки функции в треугольнике .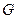

, .

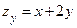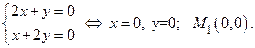
II. Отыскание критических точек функции вдоль отрезков границы.

1) 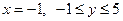. Обозначим . Критическая точка функции вдоль этой стороны − .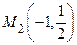

2) 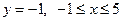. Обозначим . Критическая точка функции вдоль этой стороны − .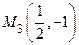

3) 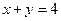, 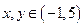. В предыдущей лекции мы нашли, что точка условного экстремума − .

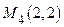III. Вершины треугольника:, , .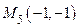

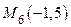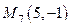IV. Отобранные точки: , , , , , , .

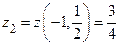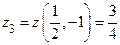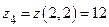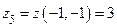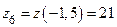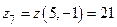V. , .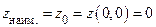

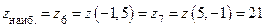Пример 2. Пусть 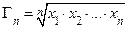− среднее геометрическое положительных чисел 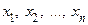и 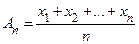− их среднее арифметическое. Доказать, что всегда справедливо неравенство .

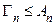Доказательство. Для доказательства требуемого неравенства можно свести её к следующей задаченайти наибольшее значение произведения положительных чисел 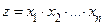при условии, что 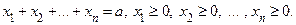. Так как

выписанные условия определяют замкнутое ограниченное множество 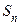в пространстве Rⁿ, то по теореме Вейерштрасса функция 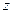принимает в некоторых точках множества 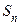свое наибольшее и наименьшее значения. Всюду на границе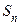 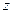обращается в нуль. Поэтому своего наибольшего значение 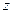достигает во внутренних точках 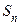. Для их отыскания применим метод неопределенных множителей Лагранжа.

Составляем функцию Лагранжа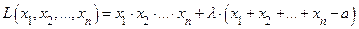

и приходим к системе уравнений

.

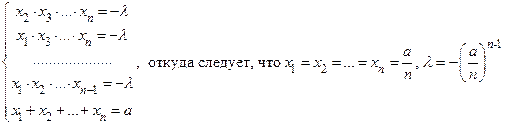Поэтому 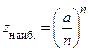или 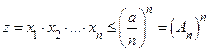. Извлекая корень степени 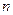из обеих частей полученного неравенства, получаем 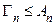. Ч и т.д.

Замечание. Применяя метод множителей, мы воспользовались только необходимыми условиями экстремума. Достаточные условия нам удалось обойти, сославшись на теорему Вейерштрасса о максимуме.

Дата добавления: 2013-12-13