Случай функции двух переменных. Метод множителей Лагранжа

Простейший пример.

Исследовать на экстремум функцию (так называемую целевую функцию )

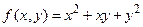
при условии, что переменные 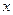и связаны уравнением

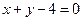
(называется функцией связи ).

Это − задача на экстремум при наличии условия связи или задача на условный экстремум в отличие от задач на безусловный экстремум, которые нам встречались раньше.

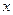Первое решение. Так как неявное уравнение связи в данном примере легко можно заменить явным выражением через переменную в виде , мы приходим к задаче на экстремум для функции одной переменной

.

Далее, как обычно, находим производные , 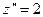. Это даёт: функция 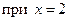имеет точку минимума, а целевая функция имеет в точке 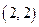условный минимум, равный .

Отметим, что безусловный минимум достигается в начале координат. Он равен нулю, т.е. меньше, чем условный минимум.

Даны две функции: 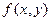− целевая функция и 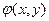− функция связи. Кривую с уравнением 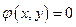мы будем называть линией связи и обозначать .

Определение. Точка 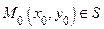называется точкой условного максимума функции при выполнении условия связи 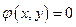, если в некоторой окрестности 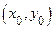для всех других точек , выполняется неравенство . Ясно как определить условный минимум, условный экстремум.

Предположим, что функции принадлежат классу 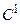в окрестности точки 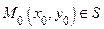, и что 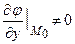. Образуем так называемую функцию Лагранжа .

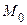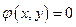Теорема 1. (Необходимое условие экстремума). Если − точка условного экстремума при условии связи , то существует значение такое, что

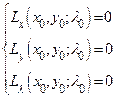. (Это ─ необходимое условие обычного экстремума функции Лагранжа.)

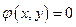Доказательство. По теореме о неявной функции существует решение уравнения связи такое, что и при этом . Обозначим 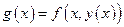. По условию теоремы 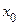− точка экстремума этой функции. Поэтому , и мы имеем

=.

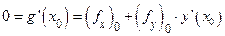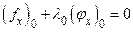Из равенства нулю определителя следует пропорциональность его строк. Поэтому существует такое число , что и или , 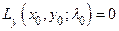. Остается заметить, что , а это равносильно равенству . Доказательство закончено.

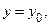
Теорема 2. (Достаточное условие экстремума.) Предположим, что 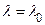выполнены необходимые условия из теоремы 1. Пусть при этом известно, что функции и 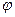принадлежат классу 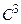в окрестности точки и 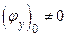. Рассмотрим квадратичную форму

,

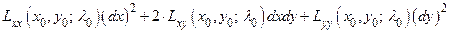где дифференциалы 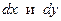связаны соотношением . Если полученная после указанной подстановки форма положительно определена, то 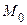− точка условного минимума. Если полученная форма отрицательно определена, то 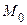− точка условного максимума. Если же эта форма знакопеременная, то в точке 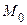нет условного экстремума.

Доказательство. На линии функции и 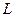совпадают, т.к. там , поэтому вместо приращения функции можно рассматривать приращение функцию Лагранжа 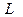на этой линии.

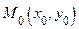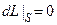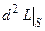Перейдем по кривой из точки в точку . При этом будет , так как по условию теоремы . Отсюда следует, что знак совпадает со знаком вблизи точки 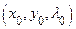. Выпишем 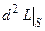, учитывая, что в точке 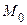будет ,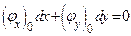

.

Поэтому, если указанная квадратичная форма положительно определена, то и 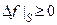вблизи т 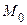, т.е. 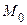─ точка условного минимума функции . Точно так же рассматриваются случаи отрицательно определённой и знакопеременной формы.

Пример. Решим вторым способом задачу, с которой мы начинали тему. Снова и снова 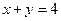. На этот раз мы применим метод неопределенных множителей. Для этого составляем функцию Лагранжа . Используем необходимые условия экстремума. Так как , , 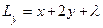приходим к системе

. Решая систему, находим , , .

Применим теперь теорему о достаточных условиях экстремума. Так как 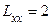, , 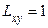, то квадратичная форма имеет вид . Учитывая, что из уравнения связи следует равенство 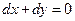или , получим 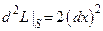. А так как 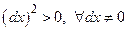, то мы снова видим, что 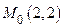− точка условного минимума.

Обобщение. Сходные формулировки необходимого и достаточного условий экстремума справедливы и в случае целевой функции 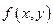, где Rⁿ, R^m. В этом случае условия связи 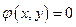− это уже система из 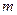уравнений: . Вместо условия , приходится требовать, чтобы определитель матрицы был
отличен от нуля. Наконец, функция Лагранжа содержит 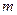неопределенных коэффициентов. Именно, .

В этих предположениях, если целевая функция 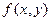имеет экстремум при условиях связи 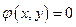в точке 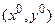, то найдётся набор чисел такой, что

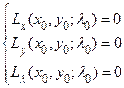(необходимое условие экстремума при наличии связей).

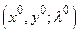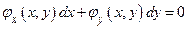Достаточный признак условного экстремума состоит в положительной (отрицательной) определённости второго дифференциала функции Лагранжа в точке при условии, что связаны условиями , вытекающими из равенства .

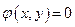Добавление. Можно доказать, что достаточный признак условного экстремума приводит

к правилу, подобному критерию Сильвестра.

Докажем, например, что следует рассмотреть определитель

,

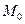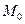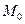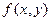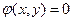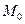где – точка, где выполняется необходимое условие экстремума. При этом, если , то – точка условного минимума, т.е. в точке – функция имеет максимум при условии связи , а если , то – точка условного минимума.

Действительно, при услови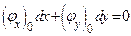и или (по условию теорем 1 и 2 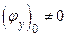) выражение

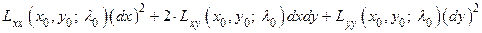
приобретает вид

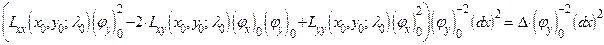, так как

.

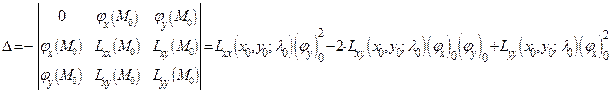Таким образом, наличие экстремума и его вид зависит от знака .

Напоследок снова обратимся к рассмотренному ранее примеру. В данном случае . Поэтому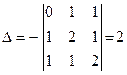

Так как , то мы приходим к тому же выводу, что и прежде: 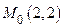− точка условного минимума функции при условии .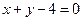

Дата добавления: 2013-12-13