Лишково - Хеммінгові і лишково-матричні коди

У лишково - Хеммінгових (ЛХ) кодах, як і при контрольному додаванні, двійкові базові кодові слова розбиваються на n b − розрядних узагальнених символів і записуються у вигляді α₁, α₂,..., α _n, де α _i ≤ 2 ^b – 1, а
N = bn. Так само, як і в двійковому коді Хеммінга (класична форма запису коду) узагальнені символи з номерами 2 ^j (j = 0, 1,…) є перевірочними, решта символів - інформаційні. Причому для отримання перевірочних символів при кодування використовується алгоритм, аналогічний алгоритму для двійкового коду Хеммінга, тобто для отримання першого перевірочного символу необхідно скласти по деякому модулю (одержати лишки) всі узагальнені символи, що мають в коді свого номера одиницю в першому (молодшому) розряді; для отримання другого перевірочного символу - скласти по модулю усі символи, що мають в коді свого номера одиницю в другому розряді і т.д.

Як модуль для отримання контрольних символів необхідно використовувати величину s = 2 ^b, тобто

α₁ = {α₃ + α₅ + α₇ + ………………} _{s ,}

α₂ = {α₃ + α₅ + α₆ + α₇ + …………} _{s ,}

………………………………

При декодування зберігається той же алгоритм розрахунку перевірочних α _i символів, що і при кодуванні, без використання в модульному складання контрольних символів. Знов одержані перевірочні символи порівнюються з відповідними перевірочними символами, обчисленими при кодувань. При їх відповідності робіться висновок про відсутність спотворення, в решті випадків - про наявність спотворення.

Якщо приписати результатам порівняння значення 0, а результатам не порівняння - значення 1, то одержана сукупність нулів і одиниць утворює код, який також, як і в двійковому коді Хеммінга, є номером спотвореного символу.

Приклад. Хай необхідно закодувати ЛХ-кодом восьми розрядну
(M = 8) послідовність 10001101 Якщо код орієнтований на виправлення двократних спотворень, то b = 2, а s = 4. Кількість узагальнених символів
m = M / b = 4. Відомо, що при цьому потрібно три перевірочні символи α₁, α₂, α₄, а інформаційними символами є α₃ = 10, α₅ = 00, α₆ = 11, α₇ = 01. Для отримання першого перевірочного символу складемо по модулю чотири α₃, α₅, α_7.

α₁ = {α₃ + α₅ + α₇}₄ = 11

Аналогічно цьому

α₂ = {α₃ + α₆ + α₇}₄ = 10,

α₄ = {α₅ + α₆ + α₇}₄ = 00.

Після кодування одержано код

11. 10. 10. 00. 00. 11. 01 = α₁, α₂, α₃, α₄, α₅, α₆, α₇,

який повинен бути записаним в ЗП, переданим в канал зв’язку і т.д.

Хай зчитаний або прийнятий з каналу зв’язку код має спотворення у п’ятому символі:

α₁, α₂, α₃, α₄, ά₅, α₆, α₇ = 11.10.10.00.01.11.01.

Після обчислення нових контрольних символів, одержимо

α₁ = {α₃ + ά₅ + α₇}₄ = 00 (11)→1,

α₂ = {α₃ + α₆ + α₇}₄ = 10 (10) →0,

α₄ = {ά₅ + α₆ + α₇}₄ = 01 (00) →1.

Результати порівняння дадуть код 101, оскільки перший а третій перевірочні символи не співпадають. Це свідчить об виявлення помилки в п’ятому символі, що і було насправді.

Неважко визначити і величину спотворення. Насправді, будь-який з перевірочних символів, наприклад α_i, при спотворень будь-якого інформаційного, наприклад α_j, що приймає участь у формуванні символу α_i має величину

ά _і = {α _c + α _d + …… + { α_j + Δα_j } + ……}_s = { α_і + Δα_j } _s. (1)

Звідки

Δα_j = {ά _i − α _i } _{s .} (2)

Для вищерозглянутого прикладу

Δα₅ = {ά₁ – α₁}₄ = {00 − 11}₄ = 01

або

Δα₅ = {ά₄ – α₄}₄ = {01 − 00}₄ = 01.

Знаючи величину (ά _i) і місце спотворення (i), легко здійснити корекцію, оскільки з (2) слідує

Α_i = { ά_i − Δα_j } _{s .}

У нашому прикладі

α₅ = {ά₅ – Δα₅}₄ = {01 – 01}₄ = 00.

Алгоритм декодування ЛХ − коду може бути спрощеним, якщо при кодуванні замість перевірочних символів α_i в записану або передану послідовність записувати величину

Δα _і = { s − Δα_j } _s.

а при декодуванні використовувати алгоритм, повністю відповідний алгоритму Хеммінга, тобто включати в перевірку і необхідні перевірочні символи.

Тоді для вже розглянутого прикладу Δα₁ = 01, Δα₂ = 10, Δα₄ = 00 необхідно записати (передати) код

α₁, α₂, α₃, α₄, α₅, α₆, α₇ = 11. 10. 10. 00. 00. 01. 11.

Якщо зчитано або прийнято слово з тим же спотворенням, що і раніше, тобто

α₁, α₂, α₃, α₄, ά₅, α₆, α₇, = 11.10.10.00.01.01.11,

то після декодування отримаємо

Δ α ₁ = { α ₁ + α₃ + ά₅ + α₇}₄ = 01,

Δ α ₂ = { α ₂ + α₃ + α₆ + α₇}₄ = 00,

Δ α ₄ = { α ₄ + ά₅ + α₆ + α₇}₄ = 01.

При цьому, якщо відмінним від нуля перевірочним символам приписати значення 1, а іншим - код 0, то одержимо код синдрому S = 101, що визначає місце спотворення, величина якого дорівнює значенню будь-якого ненульового перевірочного символу. Для розглянутого прикладу величина спотворення
Δα _і = 01, корекція якого нескладна.

У лишково − матричних кодах початковий код розбивається на узагальнені символи, які зводяться в прямокутну матрицю розмірності mn (m стовпців і n рядків) вигляду

.

Ця матриця при кодуванні розширюється на один рядок і один стовпець за рахунок перевірочних символів, кожний з яких є доповненням до s суми по модулю s елементів відповідного рядка або відповідного стовпця, при цьому одержують нову матрицю

Одержана розширена матриця записується в ЗП (передається в канал зв’язку). При декодуванні ті перевірочні елементи з додаткових рядка і стовпця, які відповідають рядку або стовпцю, що містить спотворені символи, відрізнятимуться від нуля, що дає можливість визначати місце спотворення. Якщо спотворений тільки один елемент в рядку і стовпці, то ненульове значення відповідних перевірочних символів визначить величину цієї помилки. У цьому значенні можливості ЛМ-коду до відношенню до узагальнених символів повністю співпадатимуть з можливостями по виявленню і виправленню спотворень двійкового матричного коду по відношенню до двійкових символів.

Приклад. Хай необхідно закодувати ЛМ-кодом восьми розрядну послідовність 10.00.11.10 Для b = 2 і s = 4 одержимо матрицю

= .

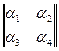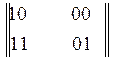Після кодування розширена матриця має вигляд

=

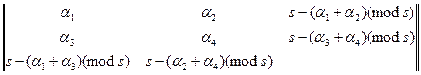Хай зчитана (прийнята з каналу зв’язку) послідовність, що відповідає матриці (спотворений елемент першого рядка другого стовпчика)

.

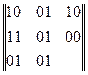В результаті декодування, одержуємо матрицю

,

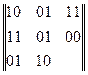з якої виходить, що спотвореним є елемент першого рядка і другого стовпця, а величина спотворення дорівнює 01. Після чого корекція спотворення стає тривіальною.

Дата добавления: 2014-01-04