Використання z - алгоритму

Для виявлення помилок в z - алгоритмі використовується відмічений вище факт, що спотворене число виходить за межі робочого діапазону, тобто

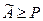. (2)

Скористаємося відомим з співвідношенням для перекладу чисел із CЛК в позиційну систему числення

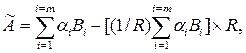(3)

де В_і – константа системи обчислення, її ортогональний базис, причому

В_і = R· m_i / p_i (i = 1, 2,..., m + 1) (4)

(m + 1) - число умовних основ, включаючи контрольну;

m_i - ціле позитивне число, зване “вагою” ортогонального базису В_і таке, при якому

В_і (mod p_i) = 1.

Підставивши вираз (3) в (2) із врахуванням (4), отримаємо

> R/p_k. (5)

Скоротивши обидві частини (5) на R отримаємо

z < 1/ р_k (6)

де

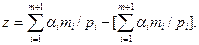(7)

Вирази (6, 7) визначають z -алгоритм декодування для ЛУ-коду. Цей алгоритм включає (m + 1) незалежне (при необхідності одночасне) множення коди i -ої групи (i = 1,..., m +1) на відповідну константу і потім складання (m +1) отриманих добутків.

Для побудови алгоритму, здатного не тільки виявляти але і виправляти помилки використовуємо наступні міркування.

Оскільки помилка по i - тій основі, як показано вище, має величину
Δ А = l_i·R_i = l_i·R/p_i те очевидною є нерівність

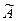– l_i·R_i < Р (8)

причому величина l_i визначається з виразу

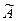[/ R_i ] = [(A + l_i·R_i) / R_i ] = l_i. (9)

Тоді з врахуванням (3, 7, 9) вираз (8) прийме вигляд

z · p_i – [ z · p_i ] < p_i/р_к. ( 10)

Ясно, що вираз (8) і еквівалентний йому вираз (10) справедливі тільки для тієї основи p_i, в залишку якої є спотворення. Отже, вираз (10) дозволяє визначити місце (номер групи), де виникла помилка. Неважко переконається, що величина цього спотворення

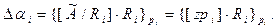(11)

Таким чином, вирази (7, 10, 11) визначають z - алгоритм декодування для
ЛУ-коду, що коректує.

Власне виправлення зводиться до операції

,

причому оскільки залишки по будь-яких основах є рівноправними, то все вище сказане відноситься і до контрольної основи. Прийнявши на етапі кодування α _k = 0, отримаємо

α _k = (р_k - P ·[z· р_k ]) (mod р_k) (12)

і тоді вирази (7, 12) визначають z - алгоритм кодування. Достоїнствами
z -алгоритма є:

1) можливість паралельного обчислення величини z;

2) простота алгоритму;

3) всі величини алгоритму є детермінованими, тому виявлена помилка виправляється з вірогідністю, що дорівнює одиниці;

4) місце і величина помилки визначаються з розрахункових співвідношень;

5) розрядність використовуваних констант значно менша, ніж в алгоритмі нулізації і лише декілька перевищує розрядність контрольної основи р_k.

До недоліку z - алгоритму слід віднести наявність у виразах (6, 7, 10) серед операцій z -алгоритмів кодування-декодування операції ділення на числа, що є простими, коли результат ділення може бути, найчастіше, нескінченним дробовим числом. Це, в наслідок обмеженої розрядності сучасних пристроїв, а отже наявності вимушених округлень результатів, може привести до неточних обчислень і поставити під сумнів трете достоїнство алгоритму.

Розглянемо приклади використання z - алгоритму стосовно умов прикладів 2, 3, розрахувавши заздалегідь константи, необхідні для обчислення змінних z. Для вибраних р ₁ = 4, р ₂ = 5, р ₃ = 7, р_k = 71 отримаємо: Р = 4·5·7 = 140; R =Р· р_k = 9940.

При цьому R₁ = 2485; R₂ = 1988; R₃ = 1420; R₄ = Р = 140, m₁ = 1; m₂ = 2; m₃ = 6;
m₄ = 3. Позначивши значення m_i / p_i, як g_i отримаємо:

g ₁ = 0,25; g ₂ = 0,4; g ₃ = 0,85714; g ₄ = 0,492957

Приклад 4. Закодувати послідовність 11.01.10 з використанням z -алгоритма ЛУ-коду. Приймемо на етапі кодування α₄ = 0. З виразу (7) отримаємо

Z = ]α₁·В₁ + α₂·В₂ + α₃·В₃ + α₄·В₄[ = ]3·0.25 + 1·0,4 + 2·0,857142 + 0·0,492957[ = ]2,86428[ = = 0,86428,

де знак ] х [ означає обчислення дробової частини від величини х.

Тоді відповідно до (11)

α₄ = (р ₄ - P·[z· р ₄]) (mod р ₄) = (71 - 140·[0,86428·71]) (mod 71) = 51.

Порівнюючи набутого значення α₄ з результатами розрахунків в прикладі 2 переконуємося в їх ідентичності.

Приклад 5. Виявити і виправити помилку в послідовності, використовуваній в прикладі 3, де 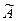= 11.01.01.0110011. Як і в прикладі 4 отримуємо

Z = ]3·0.25 + 1·0,4 + 1·0,857142 + 51·0,492957[ =
= ]27,147949[ = 0,147949.

Оскільки відповідно до виразу (6)

z = 0,147949 > 1/ р_к

то робимо вивід про наявність помилки в представленій кодовій послідовності.

Для знаходження місця спотворення оцінюємо справедливість нерівностей (10).

z ·p₁ – [ z ·p₁] = 0,91796 < p ₁ /р_к = 0,09859

Нерівність не справедлива.

z ·p₂ – [ z ·p₂] = 0,739745 < p ₂ /р_к = 0,070422

Нерівність не справедлива.

z ·p₃ – [ z ·p₃] = 0,035643 < p ₃ /р_к = 0,09859

Нерівність справедлива.

Звідси слідує вивід про спотворення в третій групі розрядів величиною

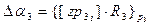= {[1,035623]·1420} ₇ = {1420}₇ = 6

тому

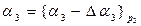= {1 -6} ₇ = 2 = 10₍₂₎.

Порівнюючи набуте значення α₃ з початковим (приклад 3) переконуємося в правильній корекції виявленого спотворення.

Приклади 4 і 5 підтверджують як відмічені достоїнства z – алгоритму, так і його недолік – наявність операцій обчислення і порівняльна багаторозрядних, можливо нескінченних величин.

Дата добавления: 2014-01-04