Алгоритм нулізації

Суть алгоритму нулізації зводиться до того, що як при кодуванні, так і при декодуванні по першим m лишкам α _i (i = 1, 2,..., m) із спотвореного числа

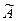= (α₁, α₂..., { α _i + Δα _i } (mod p_i),…, α _m, α _k)

послідовно формуються, так звані мінімальні числа вигляду

t₁ = (α₁, , ,_{..., ,} ),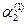

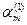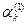t₂ = (0, (α₂ – 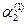) (mod p ₂), _,…, ,),

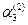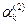t₃ = (0, 0, (α₃ - 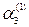- 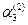) (mod p ₃), _., ,),

........................

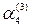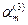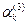t _n = (0, 0, 0...,(α _n - 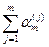) (mod p_m),),

де t_і (наприклад, t₃) – мінімальне із усіх можливих чисел, які мають лишок по основі p_і (наприклад, р ₃) такий, що на і – тому кроці нулізації дорівнює різниці по відповідному модулю між початковим значенням цього символу (наприклад, а ₃) і сумою значень символів із цим же номером, які одержані на попередній кроках (наприклад, 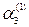+ 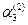). Звернемо увагу також на те, що оскільки на цьому кроці нулізації усі символи із номерами (наприклад, із = 1, 2) дорівнюють нулю, то це означає, що відповідне мінімальне число є кратним усім p_і із номерами (наприклад, р _1, р ₂), тобто є кратним добутку 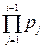(наприклад, р _1∙ р ₂).

Звернемо увагу на те, що кількість нулів в представленні мінімальних чисел послідовно збільшується, звідки і витікає назва алгоритму.

Cума мінімальних чисел Т = 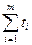має наступні дві властивості. По-перше, лишки цієї суми по всіх основах, окрім р_k завжди дорівнюють лишкам початкового числа Р. По-друге, відомо, що величина цієї суми завжди менше величини робочого діапазону Т < Р, тобто величина Т лежить а межах робочого діапазону і для неспотворених чисел Т = А.

Неважко помітити, що в останньому випадку в разі відсутності спотворень Т = А процес одержання величини α _k є процесом кодування початкового числа ЛУ-кодом, оскільки значення А залежить тільки від цього початкового числа і не залежить від невідомої при кодуванні величини лишку по контрольному модулю р_к (це означає, що знати значення α _к до кодування не має потреби). Цей лишок (шукана контрольна ознака) α _к формується як сума по модулю р_к проміжних величин t _і (і = 1, 2,..., n) чи їх лишків по основі р_к, тобто

α _k = 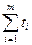(mod р_к) = 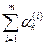(mod р_к).

Після кодування цілком сформоване число як набір лишків по усім основам, включаючи контрольну:

А = (α₁, α₂..., { α _i + Δα _i } (mod p_i),…, α _m, α _k)

передається в канал.

При декодуванні по прийнятому, можливо спотвореному числу 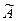знову формується величина T, яка віднімається з числа 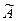. Це приводить до того, що отримана різниця

Г = 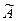– T = (0, 0, 0...,, γ) = k ∙ Р

має по всіх основах, окрім контрольної, лишки, що дорівнюють нулю, а по контрольній

γ = (α _k – (Т mod р_к)) (mod р_к) = (k∙Р) (mod р_к),

тобто

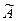- T = (0, 0., 0,...,0, (k ·Р) (mod р_к)),

де k може приймати будь-яке значення із діапазону k = 0, 1, 2,..., р_k –1.

Для неспотворених чисел, тобто при k = 0, величина γ = 0, для спотворених − γ ≠ 0. Вище доведено, що при р_k ≥ 2· р_m·p_{m -1} є взаємно однозначна відповідність між величиною помилки Δα _i і величиною γ, що дає можливість, отримавши γ, визначити місце і величину помилки, тобто здійснити її виправлення.

Недоліками цього алгоритму є:

1) обчислення величини T здійснюється послідовно, оскільки значення чергової величини t_j може бути визначеним тільки при відомих попередніх t_i (і = 1, 2,..., j -1), що виключає можливість розпаралелювання процесу і досягнення при цьому високої швидкодії алгоритму;

2) багаторозрядність мінімальних чисел t_j, оскільки перше мінімальне число потребує N розрядів, друге – (N – b)..., m - не – (N – (m – 1)∙ b) розрядів, що вимагає наявність ЗП великій ємності;

3) відсутність розрахункових співвідношень між Δα _i і γ, що потребує використовувати таблиці відповідності типу (γ→ Δα _i).

Для ілюстрації можливостей алгоритму розглянемо два приклади.

Приклад 2. Хай необхідно закодувати з використанням алгоритму нулізації початковий код 110110, вважаючи, що можлива тривалість пакету спотворень b = 2. Тоді можливе розбиття початкового коду на три (n = 3) дворозрядні групи α₁ =11, α₂ =01, α₃ =10, s = 4, а як умовні основи можна вибрати р₁ = 4, р₂ = 5, р₃ = 7. При цьому значення контрольної основи (р_к > 2· р_n ·р_{n -1} = 2·5·7 = 70) можна вибрати р_к = 71, що вимагає для свого відображення семи розрядів. В результаті цього для кодування формується код

А = 11.01.10.0000000.

Перше мінімальне число t ₁ повинне мати залишок по першій основі, який дорівнює 11₍₂₎= 3₍₁₀₎. Таким числом є t ₁ = 3 або при представленні в СЛК з вибраними основами

t ₁ = 11.11.011.0000011.

Друге мінімальне число t ₂ повинне мати залишок по першій основі, рівний нулю (тобто число, яке є кратним 4), а по другій

((α₂ - 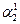) (mod p₂) = (1 – 3) (mod 5) = 11₍₂₎.

Мінімальним числом, що має такі залишки по першій і другій основах, є t ₂ = 8, тобто

t ₂ = 00.11.001.0001000.

Третє мінімальне число t ₃ повинне мати нульові залишки по перших двох основах (тобто число, яке є кратним 20), а по третьому

((α₃ - 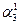- 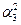) (mod p ₃) = (2 – 3 - 1) (mod 7) = 5 = 101₍₂₎.

Мінімальним числом, що має такі залишки, є t ₃ = 40, тобто

t ₃ = 00.00.101.0101000.

Тоді сума цих чисел Т= 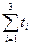рівна 51, тобто

Т = 11.01.10.0110011.

Код Т = А є шуканим результатом кодування.

Звернемо увагу на те, що величини t ₁, t ₂, t ₃ формуються послідовно, а також на їх велику розрядність.

Приклад 3. Декодувати з використанням алгоритму нулізації для умов прикладу 2 код 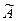= 11.01.01.0110011, в якому спотворена третя пара розрядів. Як і раніше

t ₁ = 11.11.011.0000011 = 3₁₀.

t ₂ = 00.11.001.0001000 = 8₁₀.

Для третього мінімального числа t ₃

((α₃ - 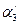- 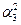) (mod p ₃) = (1 – 3 - 1) (mod 7) = 4 = 100₍₂₎.

Мінімальним числом (тобто числом, яке є кратним 20), що має такі залишки, є t ₃ = 60, тобто

t ₃ = 00.00.100. 0111100

При цьому

Т = 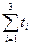=71,

тобто оскільки Т (mod 71) = 0, то

Т = 11.01.01.0000000

і

γ = (α _k – (Т mod р_к)) (mod р_к) = (0110011 - 0000000) (mod 71) = 51.

Оскільки γ ≠ 0, то робиться вивід про наявність в декодованому числі помилки. Оскільки, при цьому

γ = (k · Р) (mod р_к) = (k ·140) (mod 71),

то k = 10, тому що 1400 (mod 71) = 51.

Нескладно переконатися в тому, що декодоване число A = 1471 може бути отримано тільки в результаті спотворення початкового числа А = 51 на величину
Δ А = 1420 = = 00.00.110.0000000, тобто при спотворенні третьої групи розрядів на величину Δα₃ = 110, після чого корекція результату здійснюється просто:

α₃ = (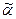₃ - Δα₃) (mod 7) – (1 – 6) (mod 7) = 2 = 10₍₂₎.

Порівнявши набутого значення з початковим, неспотвореним (умова прикладу 1), переконуємося в тому, що корекція проведена вірно.

Дата добавления: 2014-01-04