
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Загальні відомості щодо теорії лишкових класів
|
|
|
|
Код умовних лишків (ЛУ – код) відноситься до узагальнених кодів, тобто до кодів, коли певна група двійкових символів розглядаються як один символ, чи коли один символ є багаторозрядним.
Теоретичною основою ЛУ – коду є теорія лишкових класів. З теорії лишкових класів відомо, що будь-яке ціле число можна представити у вигляді набору лишків від ділення цього числа на набір взаємно простих чисел, які мають назву основ системи числення, – pi, де і = 1, 2., т, т – кількість таких основ. Вибір величини т здійснюється з умови, які викладені нижче. Тоді будь-яке число А представляється як:
А = α1, α2., α т, (1)
де:
α i = А – [ А/pi ] ∙pi,
а знак [ А/pi ] означає операцію обрахування цілої частини від дробового числа А/pi.
При цьому між числами А і їх представленням (1) існує взаємна однозначна відповідність, якщо і числа і результати операцій над ними є цілими числами і не перевищують величини так званого робочого діапазоні:
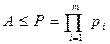 .
.
У цьому виразі величина Р [0, P) – діапазон представлення або робочий діапазон чисел. Звернемо увагу на те, що у виразі (1) α і є групою двійкових розрядів, кількість яких не перевищує розрядності відповідної основи pi.
Приклад. Нехай потрібно представити число А = 7 в системі лишкових класів із основами p 1 =2, p 2 =3, p 3 =5. В цьому разі  . Тоді
. Тоді
α1 = 7 – [7/2] ∙ 2 = 1, α2 = 7 – [7/3] ∙ 3 = 1, α т = 7 – [7/5] ∙ 5 = 2 і тоді це число запишеться як:
А = 7 = 1, 1, 2,
якщо ж В = 3, то це число запишеться як:
В = 3 = 1, 0, 3.
В системі лишкових класів усі арифметичні операції над числами виконуються шляхом паралельних операцій над кожним із лишків по відповідним модулям. Будемо ці операції, наприклад, операції над числами А та В по модулю d позначати як: 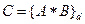 . За рахунок розпаралелювання операцій загальна швидкість їх виконання значно перевищує швидкість операцій над числами в позиційних системах числення.
. За рахунок розпаралелювання операцій загальна швидкість їх виконання значно перевищує швидкість операцій над числами в позиційних системах числення.
Операції додавання та віднімання виконуються за правилами:
 ,
,
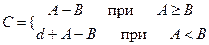
Операції множення виконуються за правилами:
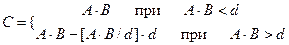
Операції ділення 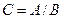 може бути виконаною при умовах, якщо, по-перше, в лишках, якими представлений знаменник відсутні такі, що дорівнюють нулю (на нуль ділити неможливо), а по-друге, величина А ділиться на В націло. В цих випадках ділення здійснює виконуються за правилами:
може бути виконаною при умовах, якщо, по-перше, в лишках, якими представлений знаменник відсутні такі, що дорівнюють нулю (на нуль ділити неможливо), а по-друге, величина А ділиться на В націло. В цих випадках ділення здійснює виконуються за правилами:
 ,
,
де d = 0, 1, 2, …, поки не буде одержано ціле значення С.
Приклад. Здійснити арифметичні операції над числами А = 7 = 1, 1, 2 та
В = 3 = 1, 0, 3. Тоді
А + В =7 + 3 = 10 = 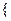 1 + 1
1 + 1 2,
2, 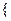 1 + 0
1 + 0 3,
3, 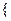 2 + 3
2 + 3 5 = 0, 1, 0,
5 = 0, 1, 0,
А – В =7 – 3 = 4 = 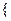 1 – 1
1 – 1 2,
2, 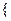 1 – 0
1 – 0 3,
3, 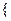 2 – 3
2 – 3 5 = 0, 1, 4,
5 = 0, 1, 4,
А · В =7 · 3 = 21 = 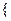 1 · 1
1 · 1 2,
2, 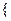 1 · 0
1 · 0 3,
3, 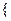 2 · 3
2 · 3 5 = 1, 0, 1.
5 = 1, 0, 1.
Спроба ж розподілити А на В буде невдалою, тому що, по-перше, результат ділення не є цілим числом, а, по-друге, по основі 3 буде ділення на нуль, що є не припустимим. Це є певним недоліком системи числення, який долається за рахунок застосування спеціальних програмних методів ділення чисел. З урахуванням того, що сама по собі операція ділення в позиційних системах числення є дуже довгою (потребує багато мікрооперацій), а швидкість операцій в системі лишкових класів є суттєво вищою, загальний час виконання ділення може бути навіть меншим ніж при використанні позиційних систем числення.
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 372; Нарушение авторских прав?; Мы поможем в написании вашей работы!