
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Анализ движения жидкой частицы
|
|
|
|
Рассмотрим виды движения, в которых может принимать участие жидкая частица.
На рис.26 показана траектория, по которой движется частица в виде кубика а. Как и твердое тело, частица может двигаться поступательно (рис.26, 1) и вращаться вокруг мгновенной оси с угловой скоростью  (рис.26, 2). Но в отличие от твердого тела жидкая частица может участвовать еще в одном виде движения, который называется деформационным. В силу деформируемости жидкости жидкая частица может иметь линейные деформации (рис.26, 3), когда она сжимается или растягивается, сохраняя неизменным свой объем и углы между соседними ребрами и так называемую угловую деформацию (рис.26, 4), когда происходит скашивание углов. В общем случае движения жидкая частица может участвовать во всех рассмотренных видах движения.
(рис.26, 2). Но в отличие от твердого тела жидкая частица может участвовать еще в одном виде движения, который называется деформационным. В силу деформируемости жидкости жидкая частица может иметь линейные деформации (рис.26, 3), когда она сжимается или растягивается, сохраняя неизменным свой объем и углы между соседними ребрами и так называемую угловую деформацию (рис.26, 4), когда происходит скашивание углов. В общем случае движения жидкая частица может участвовать во всех рассмотренных видах движения.
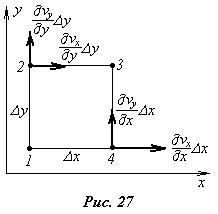
На рис.27 показана плоская частица в виде прямоугольного параллелепипеда со сторонами Dx и Dy, которую для простоты рассуждений будем рассматривать в плоском движении, зависящем только от координат x и y. Если точку 1 принять за полюс, вместе с которым частица движется поступательно со скоростью, имеющей проекции на оси координат vx и vy, то можно показать, что в общем случае точки 2 и 4 частицы имеют дополнительные скорости относительно полюса, проекции которых на оси координат показаны на рис.27. Используя эти значения скоростей, можно получить выражения для деформационного и вращательного движения жидкой частицы. При этом в гидромеханике принимаются во внимание не сами величины деформаций, а скорости деформаций.
 А). Линейные деформации возникают, в случае, когда
А). Линейные деформации возникают, в случае, когда
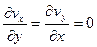 .
.
Оставшиеся составляющие скорости 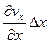 и
и  приводят к тому, что частица деформируется вдоль оси x (скоростью
приводят к тому, что частица деформируется вдоль оси x (скоростью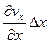 ) и вдоль оси y (скоростью
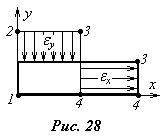
) и вдоль оси y (скоростью  ), то есть происходит линейная деформация (рис.28). Скорости линейной деформации выражаются обычно относительной величиной скорости, отнесенной к первоначальному размеру грани, вдоль которой происходит деформация. Тогда относительная скорость линейной деформации вдоль соответствующих осей записываются как
), то есть происходит линейная деформация (рис.28). Скорости линейной деформации выражаются обычно относительной величиной скорости, отнесенной к первоначальному размеру грани, вдоль которой происходит деформация. Тогда относительная скорость линейной деформации вдоль соответствующих осей записываются как
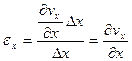 ,
,
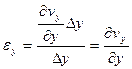 , (3.10)
, (3.10)
и, по аналогии, вдоль оси z
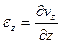 . (3.11)
. (3.11)
Если составляющие относительной скорости линейной деформации сложить, то
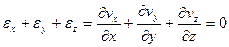 ,
,
 так как мы получили уравнение неразрывности в дифферен-циальной форме (3.7). Из полученной зависимости следует, что частица не может только растягиваться или только сжиматься в силу закона сохранения объема (3.3).
так как мы получили уравнение неразрывности в дифферен-циальной форме (3.7). Из полученной зависимости следует, что частица не может только растягиваться или только сжиматься в силу закона сохранения объема (3.3).
Б). Угловые деформации. Этот вид движения возникает, когда
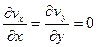 .
.
Оставшиеся составляющие скорости 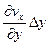 и
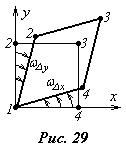
и  приводят к тому, что грани 1-2 и 1-4 начинают вращаться вокруг полюса. В результате происходит скашивание прямых углов, приводящее к угловой деформации. В результате этого частица примет форму, показанную на рис.29, жирной линией. Величину угловой деформации принято характеризовать среднеарифметическим значением угловых скоростей вращения граней:
приводят к тому, что грани 1-2 и 1-4 начинают вращаться вокруг полюса. В результате происходит скашивание прямых углов, приводящее к угловой деформации. В результате этого частица примет форму, показанную на рис.29, жирной линией. Величину угловой деформации принято характеризовать среднеарифметическим значением угловых скоростей вращения граней:
 .
.
Угловые скорости вращения каждой грани имеют вид
 ,
,
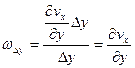 ,
,
тогда  . (3.12)
. (3.12)
В случае рассматриваемого плоского движения угловая деформация возможна только вокруг оси z, а в общем случае пространственного движения могут существовать и две другие составляющие скорости угловой деформации
 ,
,  . (3.13)
. (3.13)
В). Вращательное движение.
Если  или угловые скорости скашивания направлены в одну сторону (рис.30), биссектриса угла при полюсе начнет вращаться, то есть частица будет участвовать во вращательном движении вокруг оси проходящей через полюс. При этом угловая скорость вращения характеризуется среднеалгебраическим значением угловых скоростей скашивания. Учитывая, что положительное направление вращения вокруг оси z принято от оси x к оси y (против часовой стрелки), проекция угловой скорости вращения равна
или угловые скорости скашивания направлены в одну сторону (рис.30), биссектриса угла при полюсе начнет вращаться, то есть частица будет участвовать во вращательном движении вокруг оси проходящей через полюс. При этом угловая скорость вращения характеризуется среднеалгебраическим значением угловых скоростей скашивания. Учитывая, что положительное направление вращения вокруг оси z принято от оси x к оси y (против часовой стрелки), проекция угловой скорости вращения равна
 . (3.14)
. (3.14)
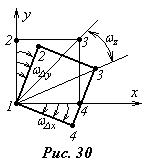
В общем случае пространственного движения могут существовать две другие составляющие угловой скорости вращения частиц:
 ,
,
 . (3.15)
. (3.15)
Если хоть одна из составляющих угловой скорости вращения частиц не равно нулю, движение называется вихревым. В противном случае, когда 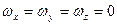 , движение называется безвихревым.
, движение называется безвихревым.
ГЛАВА IV
Динамика невязкой жидкости
|
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 1863; Нарушение авторских прав?; Мы поможем в написании вашей работы!