Интегрирование уравнений движения. Уравнение Бернулли

Дифференциальные уравнения движения невязкой жидкости в общем случае не интегрируются, но в трех частных случаях возможно получение так называемых интегралов уравнений движения. Получим один из них. Для этого будем считать движение жидкости установившимся и проинтегрируем уравнения движения (4.2) вдоль линии тока. При установившемся движении частицы жидкости движутся по линиям тока, которые совпадают с траекториями (п.3.2) и за время dt проходят путь dl=vdt или в проекциях на оси координат

, , .

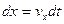Умножим каждую строчку системы (4.2) на соответственно на записанные проекции пути:

;

;

.

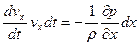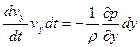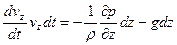Сложив левые и правые части уравнений и проведя необходимые сокращения, получим

.(4.7)

Выражение, входящее в круглые скобки, есть полный дифференциал давления

,

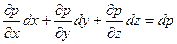а левая часть равна , так как

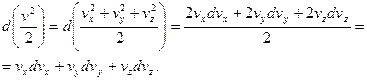
С учетом этого выражение (4.7) примет вид

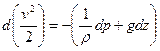, (4.8)

или, имея в виду, что r и g – величины постоянные, сумма дифференциалов равна дифференциалу суммы, выражение (4.8) можно представить в виде

.

Если дифференциал выражения равен нулю, то само выражение является постоянной величиной, то есть

. (4.9)

Умножая все слагаемые на постоянную величину r, можно получить

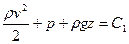, (4.10)

а деля уравнение (4.9) на постоянную g, имеем

. (4.11)

Уравнения (4.9), (4.10), (4.11) называются интегралом (уравнением) Бернулли для невязкой жидкости. Интеграл Бернулли справедлив при установившемся течении для частицы жидкости, движущейся по линии тока. Величина C (C₁, C₂) является константой только вдоль линии тока.

Выясним, каков физический смысл уравнения Бернулли. Для этого умножим каждое слагаемое уравнения (4.11) на вес частицы DG. Тогда

. (4.12)

В первом слагаемом - масса частицы. Значит, первое слагаемое 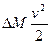представляет собой кинетическую энергию частицы жидкости.

Для того чтобы разобраться со вторым слагаемым, обратимся к рис.32. Если поместить в жидкости совершенно пустую (торичеллиеву) трубку так, что у ее основания давление равно p, жидкость поднимется на высоту и давление p будет уравновешиваться давлением столбика жидкости высотой h. Значит, второе слагаемое можно представить как работу, которую совершает давление, поднимая частицу весом DG на высоту h, или как потенциальную энергию давления.

Наконец, последнее слагаемое, как и в механике твердого тела, характеризует потенциальную энер-гию положения частицы весом DG относительно горизонтальной плос-кости сравнения, от которой рас-сматриваемая частица отстоит на z.

Следовательно, уравнение Бернулли представляет собой уравнение энергии. Чтобы от рассмотренного уравнения (4.12) снова вернуться к уравнению (4.11), необходимо (4.12) разделить на вес DG. Таким образом, уравнение Бернулли в форме (4.11) представляет собой уравнение удельной механической энергии частицы, отнесенной к ее весу. Из аналогичных рассуждений следует, что уравнение в форме (4.9) – это уравнение удельной механической энергии, отнесенной к массе, а в форме (4.10) – отнесенной к объему. Из уравнений (4.9)-(4.11) следует, что сумма трех удельных механических энергий – величина постоянная вдоль линии тока при установившемся движении невязкой жидкости.

Таким образом, уравнение Бернулли выражает закон сохранения механической энергии при установившемся движении вдоль линии тока. Каждое слагаемое в отдельности может изменяться, энергия может переходить из одного вида в другой, но их сумма должна оставаться постоянной.

В общем случае, при переходе от одной линии тока к другой, постоянная C, а значит, и величина суммарной удельной механической энергии будут меняться.

ГЛАВА V

Гидравлика

Дата добавления: 2014-01-05