Режимы движения вязкой жидкости

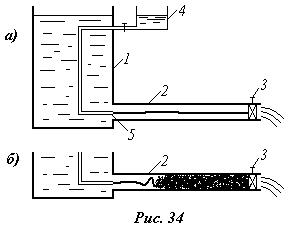
При движении вязкой жидкости, как показывает опыт, могут существовать два режима течения. Рассмотрим содержание опыта, идея которого принадлежит Рейнольдсу. Бак 1 (рис.34) заполнен жидкостью, которая может течь по трубе 2 с прозрачными стенками с различными скоростями в зависимости от степени открытости крана 3. Сосуд 4 заполнен подкрашенной жидкостью для визуализации течения основной жидкости в баке. Если скорость потока в трубе незначительна, подкрашенные частицы движутся в трубе четкой струйкой, как показано на рис.34, а. Если скорость увеличивать, то до определенного предела никаких качественных изменений не произойдет, однако, начиная с некоторой скорости, четко обозначенная струйка начнет размываться (рис.34, б) и в результате перемешивания поток жидкости в трубе оказывается подкрашенным. Случай слоистого течения без перемешивания слоев жидкости называется ламинарным режимом; случай, когда происходит интенсивное перемешивание слоев жидкости, называется турбулентным режимом.

Такого же результата, т. е. перехода из ламинарного режима течения в турбулентный, можно добиться, изменив диаметр трубы d или кинематический коэффициент вязкости n (путем подогрева жидкости). При этом переход произойдет при другой скорости течения.

Опыты показали, что переход практически однозначно определяется величиной безразмерного комплекса, называемого числом Рейнольдса

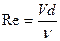, (5.2)

где в качестве характерного линейного размера принят диаметр трубы. Если Re меньше некоторого критического значения Re_кр, то режим течения ламинарный; при Re>Re_кр течение турбулентно. Опыты, проведенные при обычных условиях, дают значение критического числа Рейнольдса для круглых труб: Re_кр =2300¸2400. При числе Рейнольдса Re>Re_кр режим течения, как правило, переходит в турбулентный.

Переход ламинарного режима течения в турбулентный связан с потерей устойчивости потока. Устойчивость течения зависит не только от числа Рейнольдса, но и от интенсивности случайных возмущений, вносимых в поток. К ним можно отнести возмущения, вносимые острыми кромками, образованными входом из бака в трубу, вибраций основания и т. д. При сведении таких возмущений к минимуму критическое число Рейнольдса можно повысить на порядок. Однако вне зависимости от степени начальных возмущений при Re <2300¸2400 ламинарный режим устойчив и сохраняется в трубопроводе всегда.

Рассмотрим подробнее каждый из режимов в круглых трубах.

а) Ламинарный режим. В этом случае профиль скоростей (рис. 35) имеет вытянутую форму; на стенках трубы скорость равна нулю и достигает своего наибольшего значения V_max на оси трубы. Распределение скоростей в круглой трубе представляется параболой вида

,

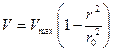где r – текущий радиус, на котором скорость равна V; r₀ – радиус трубы.

Средняя скорость, эпюра которой пока-зана на рис.35 пунктирной ли-нией равна по-ловине макси-мальной:

.

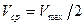Касательные напряжения при ламинарном течении определяются по формуле Ньютона (5.1). В соответствии с этим касательные напряжения на стенке t₀ определяются выражением

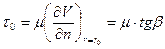, (5.3)

где b - угол между касательной к профилю скорости у стенки и нормалью к стенке (совпадает с радиусом трубы), как показано на рис.35. Характеристики ламинарного движения жидкости в трубах можно получить теоретически.

Следует подчеркнуть, что ламинарное течение при неравномерном распределении скоростей по сечению потока является вихревым. Действительно, если рассмотреть частицу, движущуюся между соседними линиями тока (см. рис.35), скорости которых неодинаковы, то станет очевидным, что из-за разницы скоростей граней частицы она начнет вращаться, как бы перекатываясь между соседними линиями тока с угловой скоростью w.

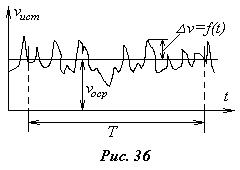б) Турбулентное движение всегда вихревое и, в результате непрерывного и интенсивного перемешивания слоев жидкости, всегда неустановившееся. Если безынерционным прибором измерить мгновенное значение скорости в какой-либо точке турбулентного потока, то можно обнаружить непрерывное ее изменение как по направлению, так и по абсолютной величине. На рис.36 представлен график зависимости величины мгновенной продольной состав-ляющей (вдоль оси трубы) скорости от времени. Эта зависи-мость случайна и чрезвычайно сложна. Турбулентное течение, как правило, характеризуется так называемой осредненной скоростью, величина которой получается осреднением мгновенной (истинной) скорости течения за достаточно большой промежуток времени T и определяется выражением

.

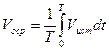Если осредненная скорость турбулентного движения постоянна, что соответствует постоянному расходу Q в трубопроводе, то такое турбулентное движение условно называется установившимся. В противном случае про турбулентное течение говорят, что оно неустановившееся. Разность между истинной и осредненной скоростями дает величину пульсации скорости

.

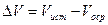Если взять сумму пульсаций скорости в точке за достаточно большой промежуток времени, то она будет равна нулю

.

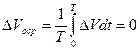Это происходит за счет взаимного уничтожения пульсаций скорости в противоположных направлениях. Если же осреднить квадрат пульсаций, то эта величина уже не будет равна нулю и может характеризовать средние по абсолютной величине пульсации скорости течения

.

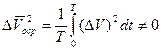Для характеристики турбулентности вводится величина степени турбулентности потока, которая выражается через осредненный по времени квадрат пульсаций

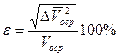. (5.4)

По абсолютной величине степень турбулентности весьма незначительна. Так, для свободных слоев атмосферы e =(0.03¸0.05)%, для потоков в аэродинамических трубах e =(0.2¸1.0)% и т. п. Однако, как показывают опыты, столь малая величина оказывает существенное влияние на характеристики турбулентного течения.

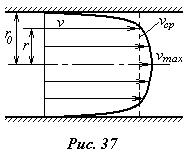На рис.37 показана эпюра осредненной скорости в трубе при турбулентном режиме течения, эта эпюра значительно «полнее» ламинарной. Выравнивание осредненных скоростей по сечению потока, приводящее к более «полной» эпюре, обусловлено интенсивным поперечным перемешиванием слоев жидкости и обменом между ними количеством движения. При ламинарном режиме обмен количеством движения идет только за счет трения слоя о слой.

Распределение осредненных скоростей в трубе круглого сечения при турбулентном потоке может быть приближенно представлено следующим степенным законом:

,

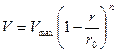где показатель степени n изменяется в пределах от 1/7 до 1/11 и тем меньше, чем больше число Рейнольдса потока.

За счет перемешивания слоев жидкости при турбулентном течении возникают дополнительные турбулентные касательные напряжения t_турб, величина которых пропорциональна пульсациям скорости. Таким образом, касательные напряжения в турбулентном потоке выражаются формулой

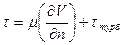, (5.5)

где первое слагаемое – обычные ньютоновские касательные напряжения, которые вдали от стенки значительно меньше t_турб. Из-за того, что касательные напряжения в турбулентном потоке выражаются формулой (5.5), а не формулой Ньютона (5.1), обычные уравнения движения вязкой жидкости неприменимы к описанию турбулентного движения.

Из-за более равномерного распределения осредненных скоростей по сечению трубы средняя скорость (пунктир на рис.37) при турбулентном режиме гораздо ближе к величине V_max по сравнению с ламинарным режимом и составляет

.

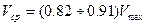В непосредственной близости к стенкам трубы перемешиванию, обуславливающему турбулентность, препятствует стенка, в результате чего у стенок в турбулентном потоке всегда есть тонкий слой жидкости, в котором движение ламинарно. Эта область ламинарного движения называется ламинарным подслоем и характеризуется его толщиной d_л. Она составляет величину долей миллиметра, но играет огромную роль в механике образования сопротивления трения трубопроводов. Толщина ламинарного подслоя, как показывают исследования, обратно пропорциональна средней скорости потока, т. е. с увеличением скорости течения толщина ламинарного подслоя уменьшается.

На рис.38 в большом масштабе показана пристеночная область потока в трубе. Турбулентный поток по поперечному сечению принято делить на две зоны – ламинарный подслой и турбулентное ядро потока. При прочих равных условиях касательные напряжения, а 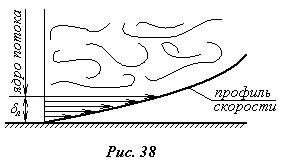значит, и сопро-тивление трения в турбулентном потоке сущест-венно больше, чем при лами-нарном. Это связано с появ-лением допол-нительных тур-булентных напряжений. На рис.39 показаны пристеночные участки ламинарной и турбулентной эпюр скоростей. Так 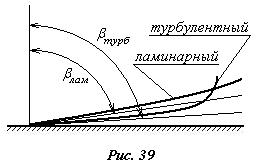как в турбулентном потоке всегда есть ламинарный под-слой, и в том и в другом случае ка-сательные напря-жения на стенке определяются по формуле Ньютона. Тогда на основании рис.39 b_турб>b_лам, а это значит, что по формуле (5.3) t_0турб>t_{0 лам}.

Дата добавления: 2014-01-05