Начальные и граничные условия

Для решения системы дифференциальных уравнений (4.2) ее следует подчинить начальным и граничным условиям. Начальные условия имеют смысл только при неустановившемся движении и характеризуют величины, входящие в систему (4.2) в начальный момент времени, т. е. в момент времени t₀ должны быть заданы v_x(x,y,z), v_y(x,y,z), v_z(x,y,z) и p(x,y,z) во всей области течения.

Граничные условия выполняются всегда, в любой момент времени, и характеризуют величины p, v_x, v_y и v_z на границах потока. Различают два вида граничных условий – кинематические, относящиеся к скоростям, и динамические, накладываемые на давления.

I. Кинематические граничные условия.

1). Условия для обращенного движения, когда на тело набегает поток со скоростью v₀ (рис.31, а).

a). Далеко от тела, там, где в жидкости не ощущается присутствие тела (теоретически на границе потока, лежащей на бесконечности) скорость жидкости равна скорости набегающего потока, то есть

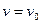при . (4.3)

Это условие называется условием отсутствия возмущений на бесконечности.

б). На поверхности тела S, которая также ограничивает поток и является непроницаемой для жидкости, нормальная по отношению к телу составляющая скорости равна нулю:

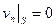. (4.4)

Условие (4.4) называется условием непротекания. Исходя из этого условия, скорость жидкости на теле касательна к его поверхности. Данное условие справедливо только для невязкой жидкости.

2). Условия для абсолютного движения, когда в покоящейся жидкости движется тело со скоростью v₀ (рис.31, б).

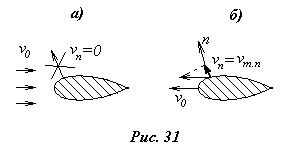
а). На большом удалении от тела (на бесконечности) скорость движения жидкости должна быть равна нулю

при . (4.5)

б). Как и в случае обращенного движения, должно выполняться условие непротекания через поверхность тела S. Это условие для нормальной скорости жидкой частицы, находящейся на поверхности тела, можно записать в виде

, (4.6)

где v_т.n – проекция скорости рассматриваемой точки тела на нормаль к поверхности в этой точке.

II. Динамические граничные условия.

1). На свободной поверхности давление жидкости принимается равным давлению, действующему на эту поверхность: p=p₀. В открытых водоемах и сосудах на свободной поверхности давление равно атмосферному: p=p_a.

2). При истечении жидкости из труб и отверстий давление в струе p принимается равным давлению в той среде, куда происходит истечение (p_сред), т.е. p=p_сред. Если струя вытекает в атмосферу, то давление в струе будет равно атмосферному.

Дата добавления: 2014-01-05