Физические теории 2 страница

2. На рис.8 показано а.т.т. произвольной формы, вращающееся вокруг вертикальной оси, закрепленной в неподвижных подшипниках, изображенных скобочками. Указаны траектории движения двух точек тела. Радиусы и плоскости окружностей, описываемых этими точками, различны, а вот центральные углы, на которые опираются дуги, описанные разными точками при вращении тела, одинаковы. Из этих рассуждений следует, что вращающееся тело имеет всего одну степень свободы: i =1. Его положение в пространстве задает одна координата - угол поворота тела j относительно некоторого положения, выбранного за начало отсчета. Закон вращательного движения выражает уравнение

j = j (t) (1.4.1)

Разность угловых координат в конечный t₂ и начальный t₁ моменты времени равна пути при вращении, измеряемом углом Dj = j₂ - j₁. Малые угловые перемещения (Dj <<2p) можно считать векторами[2], будем их обозначать 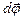. Этот вектор направлен вдоль оси в соответствии с правилом правого винта, т.е. указывает направление вращения тела, и не имеет фиксированной точки закрепления. Такой вектор называется аксиальным (осевым) в отличие от полярных векторов 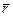,,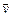 , 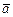рассмотренных нами в § 1.2.

Быстроту вращения характеризует угловая скорость w.

Средняя угловая скорость

<w>=Dj / Dt (1.4.2)

Мгновенная угловая скорость

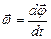(1.4.3)

Быстроту изменения угловой скорости описывает угловое ускорение e. Его среднее значение

< e > = Dw / Dt (1.4.4)

Мгновенное угловое ускорение

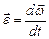(1.4.5)

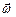и 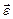- аксиальные векторы, направленные вдоль оси, как и 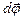. Направление вектора угловой скорости определяет правило правого винта, а направление вектора углового ускорения зависит от знака изменения угловой скорости: при ускоренном вращени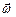и и 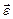направлены вдоль оси в одну сторону, при замедленном – в противоположные стороны. В СИ угловая координата измеряется в радианах (рад), угловая скорость в рад/с, угловое ускорение в рад/с².

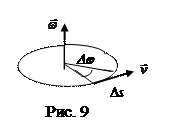3. Найдем связь между линейными и угловыми кинематическими характеристиками точки вращающегося тела. На рис. 9 показана траектория некоторой точки тела, отстоящей от оси вращения на расстоянии R, ее линейная скорость 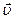и угловая скорость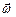. За промежуток времени Dt тело повернулось на угол Dj, а точка прошла путь Ds. Очевидно, Ds=RDj. Исходя из определений линейной и угловой скоростей (формулы 1.2.8 и 1.4.3) получаем:

υ=wR (1.4.6)

Используя формулы (1.2.13) и (1.2.15), получаем:

a_t = e R (1.4.7)

a_n=w ²R (1.4.8)

Обратите внимание, что нормальное ускорение всегда бывает у точек вращающегося тела, а тангенциальное только при неравномерном вращении.

§ 1.5. Краткие итоги главы 1.

Проследим аналогию кинематических характеристик и формул поступательного и вращательного движений.

Поступательное Вращательное

Координата s j

Путь Ds Dj

Скорость средняя < υ > =Ds / Dt <w>=Dj / Dt

Скорость мгновенная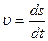

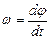
Ускорение среднее < a >= Dυ / Dt <e>=Dw / Dt

Ускорение мгновенное a_t=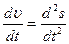

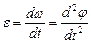
Равномерное движение

a_t= 0 e=0

υ= const w = const

s=s₀+vt j =j₀+w t

Равнопеременное движение

a_t= const e=const

υ=υ₀+a_t t w =w₀+e t

s=s₀+υ₀ t+at²/ 2 j =j₀+w₀ t+e t² /2

Подводя итог изучения Главы 1 «Кинематика», еще раз заметим, что, рассматривая движение конкретного физического тела, следует использовать такую последовательность:мы

1. выбрать систему отсчета,

2. заменить тело соответствующей моделью, сделать рисунок, поясняющий задачу,

3. определить число степеней свободы и характер движения тела и только после этого вспоминать и искать формулы.

Глава 2. Динамика материальной точки.

§ 2.1.Задача динамики. Состояние материальной точки. Динамические характеристики движения.

1. Задача динамики – найти закон движения тела, если известно, каким внешним воздействиям оно подвергается, или, наоборот, найти, каким внешним воздействиям должно подвергаться тело, чтобы выполнялся заданный закон движения. Для теоретического решения такой задачи необходимо уметь: а) задать динамическое состояние тела, б) задать внешнее воздействие, в) составить и решить уравнение динамики. Подтверждением справедливости теории является совпадение ее результатов с опытом.

2. Опыт показывает, что состояние м.т. определено, если известен ее радиус – вектор 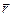и скорость 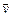. Нам это кажется очевидным, однако понимание этого появилось только в эпоху Ньютона. Еще Аристотель удивлялся тому, что топор, приставленный к полену, не оставляет на нем даже следа, а топор, с размаху ударяющий по полену, раскалывает его. Одно и то же положение топора – соприкосновение с поленом – соответствует разным его состояниям, потому что различаются его скорости. Поэтому неудивительно, что разные состояния в начальный момент ведут к разным результатам. Индивидуальной динамической характеристикой м.т. является ее масса m, так что более информативные параметры состояния м.т. - 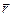и импульс 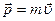(его устаревшее название – количество движения). В СИ единицей измерения импульса является 1 кг^. м/с.

Мерой воздействия служит сила 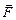, ее единица измерения в СИ называется ньютон (Н).

Уравнением динамики м.т. является второй закон Ньютона, его мы обсудим в следующем параграфе.

§ 2.2. Законы Ньютона. Второй закон как уравнение движения.

1. Первый закон Ньютона, он же закон инерции Галилея, мы уже упоминали в § 1.1. Смысл этого закона сводится к тому, что само тело изменить свою скорость не может. Первый закон Ньютона определяет инерциальные системы отсчета, и в этом проявляется его фундаментальность. Напомним, что инерциальная система отсчета вследствие принципа относительности является преимущественной, и именно для такой системы мы будем рассматривать законы динамики.

2. Второй закон Ньютона отражает утверждение опыта о том, что причиной изменения скорости тела (т.е. его ускорения) является воздействие на него другого тела. Количественно этот закон выражается формулой: 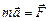. Опыт показывает (вспомните басню И.А. Крылова про лебедя, рака и щуку), что если на тело действует несколько сил, то их можно заменить одной – равнодействующей, равной векторной (геометрической сумме всех сил), так что уравнение второго закона Ньютона примет вид:

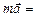S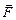 (2.2.1)

Второй закон Ньютона можно записать, используя понятие импульса тела: 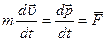. Разумеется, в правой части этой формулы стоит равнодействующая сил. Второй закон в формулировке Ньютона: «Изменение количества движения пропорционально приложенной движущей силе и происходит в направлении той прямой, по которой эта сила действует» соответствует этой формуле. Для случая постоянной силы и прямолинейного движения эта формула принимает вид:

mυ₂ – mυ₁=FDt (2.2.2)

Произведение силы на время ее действия называется импульсом силы: FDt.

3. Третий закон Ньютона отражается в известной пословице: «Как аукнется, так и откликнется». Этот закон опирается на определение силы как меры воздействия одного тела на другое и на опытный факт, что действие всегда есть взаимодействие:

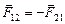(2.2.3)

Здесь индекс 12 принадлежит силе, действующей на первое тело со стороны второго, индекс 21 – силе, действующей со стороны первого тела на второе (т.е. силе противодействия первого тела). Заметим, что сила действия и сила противодействия приложены к разным телам, так что их равнодействующая не имеет смысла.

4. Законы Ньютона являются обобщением опыта, и в этом смысле они фундаментальные законы динамики. Второй закон Ньютона называют основным законом динамики м.т. или уравнением движения. Это означает, что если известны действующие на тело силы, то известно ускорение тела. Зная начальное состояние тела (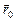, 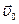), проинтегрируем уравнение второго закона Ньютона и получим скорость как функцию времени, а затем и закон движения, т.е. решим обратную задачу кинематики: , .

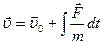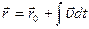Напомним, что в векторное уравнение числа подставлять нельзя, их можно подставлять только в скалярное (алгебраическое) уравнение. При решении задачи динамики чаще всего бывает целесообразно записать уравнение движения рассматриваемого тела в векторной форме, затем, выбрав подходящие оси координат, записать это уравнение в проекции на соответствующую координатную ось, и после этого интегрировать его и подставлять численные значения.

§ 2.3. Силы в механике.

1.Мерой взаимодействия тел служит сила. Физика насчитывает четыре вида фундаментальных взаимодействий. Два из них – гравитационное и электромагнитное имеют бесконечный радиус действия и проявляют себя как в макро-, так и в микромире. Еще два – сильное (ядерное) и слабое (отвечает за радиоактивный распад) вследствие малости радиуса действия проявляют себя только в микромире, спрятавшись внутри ядра атома, и поэтому в классической физике их не рассматривают. Все механические взаимодействия тел есть проявление силы гравитационной, силы упругой или силы трения. Сила трения и сила упругости имеют электромагнитную природу: все тела состоят из атомов, в состав которых входят электрически заряженные частицы.

2. Гравитационное взаимодействие представляет собой взаимное притяжение тел: две материальные точки массами m₁ и m₂ на расстоянии r друг от друга притягиваются с силой, описываемой законом всемирного тяготения:

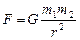(2.3.1)

G – гравитационная постоянная, она введена для согласования единиц измерения величин в обеих частях формулы, в СИ G = 6,67^.10^-11 Н^.м²/кг² = 6,67^.10^-11 м³/(кг^.с²). В форме (2.3.1) закон применим также для вычисления сил тяготения между материальной точкой и телом шарообразной формы или между двумя шарами. В этом случае r – расстояние от м.т. до центра шара, или, соответственно между центрами шаров, и сила тяготения направлена вдоль радиуса шара.

Формулы второго закона Ньютона (2.2.1) и закона всемирного тяготения содержат массу. Заметим, что в этих случаях проявляются разные свойства одного и того же тела. Во втором законе Ньютона масса инертная, измеряющая способность тела сопротивляться изменению состояния под воздействием другого тела. В законе всемирного тяготения масса гравитационная или тяготеющая. Экспериментально установлено, что эти массы равны друг другу (Р. Этвеш, 1894 г.). Этот опытный факт получил название принципа эквивалентности и лежит в основе общей теории относительности Эйнштейна (теории тяготения).

Из принципа эквивалентности, в частности, следует, что сила тяготения со стороны одного тела сообщает всем другим телам одинаковое ускорение независимо от их масс. Например, все тела притягиваются к земле, действующая на них сила тяготения называется силой тяжести. Определим ее по формуле (2.3.1): 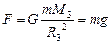. Здесь 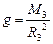– ускорение свободного падения, M₃ и R₃ соответственно масса земли ее радиус. Форма Земли отличается от шара, к тому же плотность вещества неодинакова в разных местах ее объема, но влияние этих параметров столь незначительно, что им можно пренебречь, так что во всех точках поверхности Земли g»9,8 м/с². Сила тяжести на поверхности земли выражается формулой:

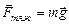(2.3.2)

Из рассмотренного понятно, почему уменьшается сила тяжести космического путешественника, значительно удалившегося от поверхности Земли, и почему на разных планетах на него будет действовать разная сила тяжести. В частности, сила тяжести на Луне почти в 6 раз меньше, чем на Земле.

3. Сила тяжести является причиной того, что отсутствие опоры (подвеса) вызывает падение тела. Сила, действующая со стороны опоры (подвеса), называется реакцией опоры и направлена всегда перпендикулярно поверхности опоры к телу, т.е. от опоры. Понятно, почему вертикальная поверхность не может служить опорой. Весом тела называется сила, с которой тело давит на опору или тянет подвес, удерживающий его от падения на землю. В соответствии с третьим законом Ньютона вес и реакция опоры (сила действия и сила противодействия) равны друг другу. Понятие невесомости означает отсутствие этих сил, в частности, стоит нам подпрыгнуть, чтобы оторваться от опоры, как мы попадаем в состояние невесомости. В течение всего времени движения, пока мы вновь не приземлимся на опору, сила тяжести не перестает действовать, замедляя движение вверх и ускоряя движение вниз, а вот вес отсутствует. Космонавты в космическом корабле, движущемся с выключенными двигателями, также находятся в состоянии невесомости. Зато при разгоне корабля они испытывают перегрузки, когда вес значительно превышает силу тяжести: реакция опоры должна не только компенсировать силу тяжести, прижимающую космонавта к сиденью, но и сообщить ускорение, направленное от земли. Впрочем, с подобными перегрузками встречаются не только космонавты.

4. Сила упругости возникает в упруго деформированном теле и противодействует внешней 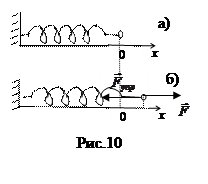деформирующей силе. Деформации, т.е. изменение расстояний между точками тела в результате внешнего воздействия, называются упругими, если они исчезают после снятия воздействия. Упругими, как правило, бывают только малые деформации. Примером служит упругая сила сжатой или растянутой пружины. На рис.10 а) показана недеформированная пружина, на рис 10 б) эта же пружина растянута внешней силой на величину x, в результате в пружине возникает . Величину упругой силы выражает закон Гука:

F= -kx (2.3.3)

k – коэффициент упругости (жесткость), постоянная для данного тела величина, в СИ измеряется в ньютонах на метр (Н/м). Знак минус указывает на противоположность направлений упругой силы и деформации.

5. Сила трения препятствует движению тела. Различают трение сухое и трение жидкое.

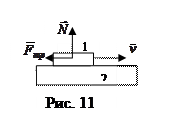Сила сухого трения возникает между твердыми телами, контактирующими друг с другом вдоль некоторой поверхности. Она вызвана тем, что шероховатости поверхности одного тела, цепляясь за шероховатости поверхности другого тела, препятствуют их скольжению друг относительно друга. Рис.11 иллюстрирует рассматриваемую ситуацию: тело 1 движется со скоростью 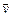по поверхности тела 2. Опыт показывает, что сила трения скольжения F_тр пропорциональна реакции опоры N и направлена в сторону, противоположную скорости:

F_тр = mN (2.3.4)

m - коэффициент трения, безразмерная величина. Его значение зависит от мате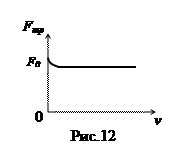риалов трущихся поверхностей, качества их обработки, загрязненности и обычно считается приблизительно постоянным для двух конкретных тел. В действительности, при стремлении скорости к нулю отмечается некоторое возрастание силы трения до значения F₀. На рис. 12 приведен график модуля силы трения скольжения от величины скорости для движения, изображенного на рис.11. Чтобы покоящееся тело 1 пришло в движение, к нему надо приложить силу, чуть превышающую F₀. Если внешняя сдвигающая сила

F< F₀ , то тело 1 останется неподвижным. Это значит, что внешняя сила не в состоянии преодолеть трение, и она уравновешивается силой трения покоя F_пок.. Из законов Ньютона следует, что сила трения покоя численно равна и противоположно направлена F_. Из сказанного ясно, что 0£ F_пок. £ F₀. Для максимальной силы трения покоя иногда пользуются коэффициентом трения покоя m₀ в формуле:

F₀=m₀N (2.3.5)

Отметим, что формула (2.3.5) и m₀ имеют смысл только применительно к максимальной силе трения покоя.

Трение жидкое или вязкое возникает при движении слоев жидкости или газа друг относительно друга. Оно встречается при движении твердого тела в жидкости или газе, а также при наличии жидкой (вязкой) смазки между трущимися поверхностями твердых тел. Особенностью жидкого трения является отсутствие трения покоя. Вам, вероятно, приходилось наблюдать, что тяжелое бревно в воде даже ребенок перемещает без труда, тогда как это же бревно, лежащее на суше, не всегда может сдвинуть даже сильный мужчина. Еще отличительной особенностью вязкого трения является возрастание силы трения с увеличением скорости, причем, для небольших скоростей эта зависимость линейная, а при больших скоростях она становится квадратичной. С силой вязкого трения мы встречаемся в ветреную погоду, плавая в воде и ныряя в воду.

§ 2.4. Работа силы. Мощность.

1. При перемещении тела под действием силы совершается работа A. Пусть под действием постоянной силы F тело прошло путь Ds в направлении линии действия силы, тогда работа силы по определению:

A= FDs (2.4.1)

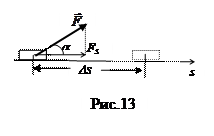Если перемещение и сила направлены под углом друг к другу (рис.13), то

A= FDs cosa =F_sDs (2.4.2)

F_s – проекция силы на направление перемещения, иногда ее называют движущей силой. Работа - скалярная величина: A>0 при условии 0 £ a £ p; A<0 при p/2 £ a £ p; A = 0 при a =p/2, т.е. сила, направленная перпендикулярно перемещению, работу не совершает. В СИ работа измеряется в джоулях (Дж): 1 Дж = 1Н^. 1с.

Если во время движения сила, а также угол a изменяются (сила переменная, траектория криволинейная), то поступают так. Разбивают путь на сумму столь малых (элементарных) участков ds, на каждом из которых сила и угол ее наклона еще не успели заметно измениться, вычисляют работу на таком элементарном участке: dA =F_sds, а затем суммируют все элементарные работы. Формула работы переменной силы при перемещении тела из точки с координатой s₁ в точку с координатой s₂::

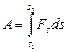(2.4.3)

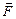Отметим, что сила и перемещение 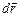- векторы, и |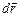| = ds, так что в формуле (2.4.3) можно использовать скалярное произведение этих векторов: F_sds=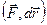. Напомним геометрический смысл определенного интеграла – это площадь, заштрихованная на рис. 14.

Работа при перемещении по траектории складывается из элементарных работ на элементарных участках траектории, каждому из которых соответствует определенное состояние тела. Любое изменение состояния называется процессом, и работа - характеристика процесса.

2. Мощность N – интенсивность совершения работы. Средняя мощность

< N >=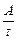 (2.4.5)

Здесь A – работа, совершенная за время t. В СИ мощность измеряют в ваттах (Вт): 1Вт=1Дж/1с. На технических устройствах и агрегатах указывают их среднюю мощность, которая реализуется при их работе. Мгновенная мощность зависит от скорости движения и равна:

N = 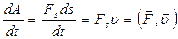(2.4.6)

Из формулы (2.4.6) следует, что мгновенная мощность мотора автомобиля при разгоне растет даже при неизменной силе тяги мотора.

§ 2.4. Механическая энергия.

1. Энергия – важная характеристика состояния тела, и она широко используется не только в физике, но и во всех других областях жизни. Энергия – физическая величина, характеризующая способность тела совершать работу. Механика рассматривает два вида энергии – кинетическую и потенциальную. Их сумма образует полную механическую энергию тела. Энергия тела уменьшается, когда тело совершает работу против внешних сил, и увеличивается, когда внешние силы совершает работу над телом. Работа – это способ изменения энергии тела, передачи энергии от одного тела к другому. Энергия и работа имеют одинаковую единицу измерения. Мы отмечали, что работа сопровождается изменением состояния тела, она – характеристика процесса. Энергия определяется состоянием тела, ее называют функцией состояния. Это означает, что изменение энергии тела при переходе из одного состояния в другое не зависит от процесса. Оно равно разности энергий тела в конечном и начальном состояниях.

2. Пусть тело перемещается под действием силы. Элементарная работа dA =F_sds =F_sds. Применив второй закон Ньютона и определение тангенциального ускорения, получаем: Fs=ma_t=mdυ/dt и далее: dA =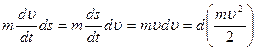. Этот результат свидетельствует о том, что работа превращается в приращение некоторой величины, соответствующей данному состоянию тела. Эту величину называют кинетической энергией тела - E_к:

E_к=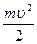 (2.4.1)

Кинетическую энергию можно выразить через характеристику состояния тела – импульс p=mv:

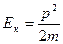(2.4.2)

Кинетическая энергия – энергия движения, она численно равна работе, которую может совершить тело до полной остановки. При перемещении тела из точки 1 в точку 2 работа внешней силы на этом пути A₁₂ равна изменению его кинетической энергии:

A₁₂=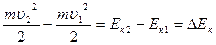 (2.4.3)

3. Существуют силы, работа которых не зависит от формы траектории, связывающей начальное и конечное положения тела. Такие силы называются консервативными или потенциальными. Поясним это рисунком 15. Тело переместилось из точки 1 в точку 2 по траектории 1а2, при этом сила совершила работу А_1а2,. При перемещении по траектории 1б2 работа равна А_1б2. По определению консервативной силы А_1а2= А_1б2. Работа силы по замкнутому пути A o (например, 1а2б1) равна нулю. Действительно, A o = А_1а2+ А_2б1= А_1а2 - А_1б2 = 0. Заметим, что при измении направления движения на противоположное (см. рис. 13) угол межде векторами силы и перемещения из острого превращается в тупой, при этом их косинусы отличаются только знаком. Это означает, что если при движении в одном направлении работа силы положительная, то при движении в противоположном направлении она отрицательная. Отсюда же следует еще одно свойство консервативной силы – равенство нулю работы по любой замкнутой траектории.

Покажем, что из трех сил – тяжести, упругости и трения первые две консервативные.

Пусть на тело действует сила тяжести, и тело перемещается из точки 1 в точку 2 (рис.16). Вектор силы тяжести m и элементарное перемещение ds (для наглядности пренебрегли математической строгостью, нарисовав его) образуют угол a. Вычислим работу силы тяжести, учитывая, что ds^.соsa=- dy: 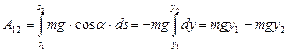. Полученный результат показывает, что работа силы тяжести выражается через характеристики состояния тела в начальном и в конечном

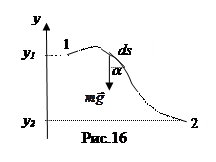его положениях, задаваемых координатами y₁ и y₂, а также показывает, что работа силы тяжести на замкнутом пути равна нулю – сила тяжести консервативная.

Аналогичный результат дает сила упругости F = -кх: 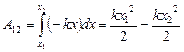, что доказывает ее консервативный характер.

Сила трения неконсервативная. Действительно, при любом направлении движения эта сила направлена против движения, ее работа на любом элементарном перемещении отрицательна, следовательно, работа на замкнутом пути не равна нулю.

4. Работа консервативной силы равна уменьшению некоторой величины, являющейся функцией состояния тела и измеряющейся в СИ в джоулях. Эту функцию называют потенциальной энергией Е_п, разность ее значений в начальном -1 и в конечном – 2 положениях тела равна работе силы при перемещении тела по любой траектории, связывающей два его положения:

А₁₂=Е_л1 – Е_п2 (2.4.4)

Оказывается, что мы уже вывели формулы потенциальной энергии. Напомним, что потенциальная энергия – это энергия взаимодействия, зависящая от взаимного положения тел. Потенциальная энергия тела в поле силы тяжести земли зависит от его высоты h над горизонтальным уровнем, принятым за нулевой, и выражается формулой:

E_п =mgh (2.4.5)

Дата добавления: 2014-01-06