Физические теории 5 страница

υ _вер=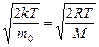 (5.5.2)

Это же распределение позволяет вычислить среднюю арифметическую < υ > и среднюю квадратичную скорости молекул υ _кв по формулам[12]: < υ >=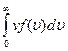 и υ _кв=. В результате

< υ >=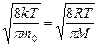 (5.5.3)

υ _кв= (5.5.4)

Обратите внимание, что средняя квадратичная скорость, рассмотренная нами ранее в § 5.2, выражается формулой, совпадающей с (5.5.4)[13]. Напомним обозначения величин: m₀ -масса молекулы, M- молярная масса, k -постоянная Больцмана, R -универсальная газовая постоянная, T -абсолютная температура.

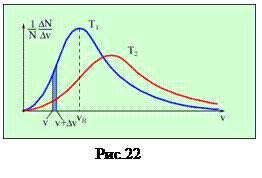2. На рис. 22 представлено распределение Максвелла молекул газа по скоростям для двух разных значений температуры, причем, Т ₁< Т ₂.На вертикальной оси отложена функция распределения f (υ)= 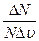(вспомните ее физический смысл). Доля заштрихованной площади под каждым графиком на этом рисунке равна доле числа молекул газа, скорости которых в данный момент времени имеют значения от υ до υ+Dυ при данной температуре Т: 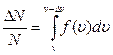(вспомните геометрический смысл определенного интеграла). Физически это означает, что при более высокой температуре молекулы начинают двигаться быстрее, и доля числа молекул в том же самом промежутке скоростей уменьшается. Общая площадь под кривой распределения всегда равна 1: действительно, 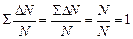. Характерные скорости теплового движения υ _вер (на графике она обозначена v₀)_, < υ >, υ _кв пропорциональны 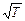. Эти закономерности отражены на графиках. Площади под ними одинаковые, тогда как график для более высокой температуры ниже и шире, его максимум смещен вправо по сравнению с графиком для температуры пониже.

3. Еще раз отметим, что распределение Максвелла выполняется для равновесного состояния газа и есть отражение статистической закономерности в молекулярном хаосе, каким является тепловое движение. Каким бы ни было исходное распределение молекул газа по скоростям, при наступлении равновесия оно станет максвелловским. Например, будем заполнять сосуд газом, впуская туда через маленькое отверстие молекулы поодиночке. Пусть все молекулы влетают с одинаковыми по величине и по направлению скоростями. Заполним сосуд, закроем его и оставим при неизменных внешних условиях. Исходное неравновесное состояние будет «забыто» газом, наступит равновесие, молекулы будут двигаться хаотически, их скорости при столкновениях будут изменяться случайным образом, но в соответствии с распределением Максвелла.

§ 5.6. Барометрическая формула. Распределение Больцмана.

1. Атмосферное давление создает сила тяжести столба воздуха, высота которого по мере подъемы над поверхностью земли уменьшается, соответственно, уменьшается атмосферное давление. Зависимость атмосферного давления от высоты над поверхностью земли выражается барометрической формулой. Получим ее, используя следующую модель:

• атмосферный воздух является идеальным газом,
• изменением ускорения свободного падения при удалении от земли в пределах земной атмосферы (ее толщина около 20 км) можно пренебречь,
• изменением температуры воздуха при удалении от земли в пределах земной атмосферы можно пренебречь (температура за бортом самолета, выполняющего полет на высоте 10 км, ниже на несколько десятков Кельвинов по сравнению с 300 К на земле).

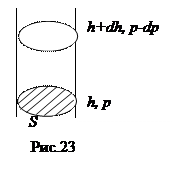Мысленно выделим из земной атмосферы вертикальный столб воздуха в виде цилиндра с площадью сечения S (рис. 23). Hа высоте h+dh атмосферное давление уменьшается на dp по сравнению с высотой h, так как на сечение S на этой высоте не давит сила тяжести массы воздуха dm, заключенного между указанными на рисунке сечениями. Пренебрегая изменением плотности газа r в элементарном объеме газа dV=Sdh, получаем: . Выражая плотность из уравнения Клапейрона - Менделеева, находим:

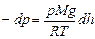. Получили дифференциальное уравнение с разделяющимися переменными. Его интегрирование дает: 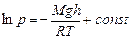. Найдем постоянную интегрирования из условия: при h= 0 p=p₀ – так обозначим давление на поверхности земли, и получим барометрическую формулу:

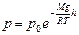(5.6.1)[14]

Вывод: атмосферное давление экспоненциально уменьшается с увеличением высоты над поверхностью земли, причем, летом это изменение происходит медленнее, нежели зимой (влияет температура Т). Физический механизм этого понятен: тепловое движение стремится «увести» молекулы как можно дальше друг от друга, и повышение температуры – меры средней энергии хаотического движения - способствует этому, тогда как сила тяжести стремится все молекулы воздуха прижать к поверхности земли. Отсутствие атмосферы на луне есть следствие того, что сила тяжести там примерно в 6 раз меньше земной.

2. Преобразуем формулу (5.6.1), учитывая, что p=nkT, Mgh/R=m₀ Nagh/R=m₀ gh/kT и потенциальная энергия частицы в поле силы тяжести E=m₀gh. Получаем формулу распределения Больцмана:

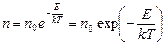(5.6.2)

Эта формула выражает зависимость концентрации частиц от величины их потенциальной энергии. Мы получили ее для частного случая поля силы тяжести. Однако эта формула применима для любого потенциального силового поля и представляет собой закон физики о распределении числа классических частиц по уровням энергии.

Действие этого закона проявляется и в социальной жизни: чем больше социальная значимость человека, измеряемая его общественной пользой, тем выше та ступенька общественной лестницы, на которой он находится, и тем меньше людей на этой ступеньке. Напомним, что энергия характеризует способность совершать работу, так что высота ступеньки общественной лестницы измеряется общественно значимой работой.

§ 5.7. Среднее число столкновений и средняя длина свободного пробега молекул.

1. Длиной свободного пробега молекулы называется путь, пройденный ей от одного столкновения до другого при хаотическом движении. Для конкретной молекулы эта длина меняется случайным образом, также случайным образом меняется число ее столкновений в единицу времени с другими молекулами. Их средние значения зависят от состояния термодинамической системы и являются выражением закономерности, которая проявляется в хаосе. Обозначим среднюю длину свободного пробега молекулы <l>, среднее число ее столкновений в единицу времени t, тогда пройденный за единицу времени средний путь, равный средней скорости < υ >, выразится так:

< υ >=< l >t (5.7.1)

2. Рассмотрим следующую модель. Пусть молекулы являются твердыми шариками диаметром d_э [15]. При столкновении молекул друг с другом расстояние между их центрами равно d_э. Пусть все молекулы, кроме одной, покоятся. Проследим ее путь за единицу времени. Он складывается из отрезков прямых (рис.24). На рисунке движущаяся молекула – черный шарик, ее траектория показана штриховой линией. При столкновении с другими молекулами (белые шарики) она изменяет направление и скорость движения. Траектория ее движения за единицу времени является осью коленчатого цилиндра длиной < υ >, радиусом d_э и объемом V= < υ > S= < υ >p d_э². Боковые стенки этого цилиндра изображены на рисунке сплошными линиями, площадь его поперечного сечения S заштрихована. Движущаяся молекула (черный шарик) столкнулась со всеми молекулами, центры которых оказались внутри коленчатого цилиндра (белые шарики), и их число N=nV равно числу столкновений молекулы с другими в единицу времени. В действительности движутся все молекулы, так что столкновений будет еще больше. Расчеты, которые мы не приводим, показывают, что их число возрастет в 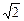раз. Таким образом, среднее число столкновений молекулы в единицу времени

t = 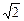n < υ >p d_э² (5.7.2)

Из формул (5.7.1) и (5.7.2) получаем формулу средней длины свободного пробега молекул:

<l>=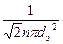 (5.7.3)

3. Проанализируем полученные нами формулы. При условиях, близких к обычным атмосферным (р» 10⁵ Па, п»10²⁵ м^-3) получаем <l>»10^-5 м, t»10⁹ с^-1. Учитывая, что давление пропорционально концентрации молекул (р=пкТ), видим, что средняя длина свободного пробега молекул растет с понижением давления. При р= 1 Па» 0,01 мм рт.ст. <l>»1 м, это значит, что в сосуде с линейными размерами порядка 1 м молекулы газа свободно летают от стенки к стенке, практически не сталкиваясь друг с другом. Такой газ называется ультраразреженным, его состояние соответствует техническому вакууму. Заметим, что в мельчайших порах материала газ находится в состоянии технического вакуума даже при атмосферном давлении.

§ 5.8. Выводы из главы 5.

В газе, находящемся в состоянии термодинамического равновесия, молекулы движутся хаотически, состояния отдельных молекул изменяются случайным образом. Однако эти случайности подчиняются определенным статистическим закономерностям, которые проявляются в характеристиках состояния всей системы. Давление и температура газа, наиболее вероятная скорость теплового движения молекул, их средняя длина свободного пробега есть интегральные характеристики всей термодинамической системы, а не отдельной частицы.

Глава 6. Термодинамика.

§ 6.1. Тепловые процессы

1. Состояние термодинамической системы (тела) изменяется при изменении внешних условий. Если после изменения внешних условий тело снова окажется термодинамически изолированным, то в нем установится новое состояние теплового равновесия. Каждому такому состоянию соответствуют свои макроскопические параметры состояния, задаваемые соответствующими особенностями теплового движения. Для идеального газа эти параметры p,V,T связаны уравнением состояния Менделеева – Клапейрона. Всякое изменение параметров состояния тела (или некоторых из них) называется термодинамическим или тепловым процессом. Законы тепловых процессов изучает термодинамика.

2. Различают равновесные и неравновесные тепловые процессы. Равновесный процесс предполагает, что при незначительном изменении внешних условий в теле успевает установиться равновесное состояние прежде, чем опять произойдет изменение внешних условий. Равновесный процесс состоит из последовательности равновесных состояний тела, т.е. в каждый момент времени состояние тела можно с требуемой точностью считать равновесным. На термодинамических диаграммах[16] равновесное состояние газа изображается точкой, а равновесный процесс - линией. Точки этой линии соответствуют промежуточным состояниям тела. Важнейшим свойством равновесных процессов является их обратимость. Обратимым называется процесс, который можно провести в обратном направлении через те же промежуточные состояния, при этом после возвращения в исходное состояние ни в теле, ни в окружающих его телах никаких изменений не останется.

Если внешние условия изменяются так быстро, что тепловое движение в системе не успевает привести ее в равновесные промежуточные состояния, то процесс называется неравновесным. Такой процесс является необратимым и его нельзя изобразить графически.

Опыт показывает, что многие практически важные процессы, используемые технической термодинамикой в тепловых и холодильных машинах, можно с достаточной точностью считать равновесными. Далее мы рассмотрим законы равновесной термодинамики.

§ 6.2. Первое начало термодинамики.

1. Внутренняя энергия U термодинамической системы (тела) складывается из кинетической энергии теплового движения его частиц, потенциальной энергии их взаимодействия друг с другом и собственной внутренней энергии частиц, имеющих определенное внутреннее строение. В модели идеального газа потенциальная энергия взаимодействия молекул пренебрежимо мала. Молекулы рассматриваются как м.т. или как их жесткие системы, так что собственная внутренняя энергия молекул не изменяется, и ее можно считать равной нулю. Внутренняя энергия идеального газа равна сумме кинетических энергий хаотического движения его молекул. Учитывая, что средняя энергия теплового движения молекулы пропорциональна температуре (формула 5.4.3), вычислим внутреннюю энергию идеального газа, состоящего из N частиц: U=N < E >=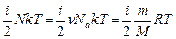. Итак, внутренняя энергия идеального газа выражается формулой:

U= (6.2.1)

Отметим, это внутренняя энергия идеального газа определяется только температурой. В каждом состоянии она имеет определенное значение, не зависящее от того, каким путем и из какого предыдущего состояния газ перешел в данное состояние. Такие характеристики состояния в физике называют функциями состояния. Отметим, что функциями состояния являются кинетическая и потенциальная энергии, рассмотренные в механике. Для функции состояния характерно, что ее изменение не зависит от процесса перехода из начального состояния 1 в конечное состояние 2 и равно разности ее значений в конечном и начальном состояниях:

D U=U₂ –U₁ (6.2.2)

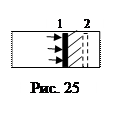2. При изменении состояния газа изменяются его параметры состояния: p,V,T (или некоторые из них). Объем газа задается положением внешних тел (объемом сосуда). На рис. 25 изображен сосуд с газом, закрытый подвижным поршнем площадью S. На поршень действует сила давления F=pS, под действием которой поршень перемещается из положения 1 в положение 2 на малое расстояние dl. При этом объем газа увеличивается на dV=Sdl (на рисунке он заштрихован), а сила давления совершает элементарную работу dA=FdS=pdV. Работа газа при изменении его объема от V₁ до V₂ равна:

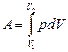(6.2.3)

При увеличении объема работа газа положительная, при уменьшении – отрицательная. Напомним, что графически работа выражается площадью под графиком процесса на pV – диаграмме.

Для совершения работы всегда требуется источник энергии, в частности, для совершения работы газ может использовать свою внутреннюю энергию: dA= - dU.

3. Пусть газ нагревается без изменения объема, т.е. механическая работа не происходит. В этом случае внутренняя энергия газа увеличивается за счет сообщения ему от внешних более нагретых тел количества тепла Q. Напомним, что средняя кинетическая энергия теплового движения молекул пропорциональна температуре. Более «горячие» молекулы внешних тел, сталкиваясь снаружи со стенками сосуда, передают через стенки более «холодным» молекулам газа дополнительную кинетическую энергию, в результате увеличивается внутренняя энергия и температура газа в сосуде. С микроскопической точки зрения процесс передачи тепла представляет собой работу по ускорению «медленных» молекул при их столкновении с «быстрыми». Этот процесс является статистическим, усредненным по всей совокупности частиц системы. Количество тепла dQ, переданное газу при элементарном процессе, алгебраическая величина: dQ >0, если оно передано извне газу, dQ <0, если оно забрано у газа. Таким образом, dU= dQ.

4. В общем случае изменение внутренней энергии газа может происходить одновременно путем совершения работы и передачи ему тепла: dU=dQ-dA. Закон сохранения энергии, учитывающий особую форму ее передачи в виде тепла, называется первым началом (законом) термодинамики. Его формулу для бесконечно малого изменения состояния тела называют первым началом термодинамики в дифференциальной форме и записывают так:

dQ=dU+dA (6.2.4)

Первый закон термодинамики в интегральной форме имеет вид: количество тепла, переданное телу, идет на изменение его внутренней энергии и на совершение механической работы против внешних сил. Его формула:

Q=DU+A (6.2.5)

Количество тепла, энергия, работа измеряются в одних и тех же единицах (в СИ это джоуль) и могут превращаться друг в друга. С точки зрения физической сути между ними существует принципиальное различие. Энергия является функцией состояния системы, тело обладает запасом энергии. Количество тепла и работа не есть функции состояния, они есть характеристики процесса. О количестве тепла и о работе можно говорить только при изменении состояния тела, применительно к ним понятие «запаса» лишено физического смысла. Количество тепла и работа есть формы изменения энергии тела. При переходе тела из одного состояния в другое его энергия изменяется одинаково при любых процессах, связывающих эти состояния, тогда как работа и количество тепла в разных процессах могут быть разными. Это отличие физического смысла отражается в формулах первого начала термодинамики: в его интегральной форме DU означает изменение (приращение) внутренней энергии, в дифференциальной форме dU -дифференциал (приращение), dQ и dA- бесконечно малые величины, а не их приращения (дифференциалы). Чтобы подчеркнуть это смысловое различие с точки зрения математики, иногда пишут dQ, dA, но dU.

Первое начало термодинамики есть закон сохранения энергии, он является фундаментальным законом природы. Его областью применения являются все тепловые процессы, происходящие в газах, жидкостях, твердых телах. Действие этого закона сопровождает нас постоянно. Например, поставим чайник на плитку. Тепло идет на нагревание воды и окружающих тел, соответственно, на увеличение их внутренней энергии. Если своевременно не снять чайник, то при кипении пар поднимает крышку, и теперь тепло идет и на совершение механической работы.

§ 6.3 Изопроцессы.

При изопроцессах во всех промежуточных состояниях термодинамической системы какой-либо ее параметр имеет неизменное значение. Рассмотрим такие процессы с точки зрения первого начала термодинамики.

1. При изохорном процессе не изменяется объем газа: V=const, а давление и температура изменяются пропорционально друг другу. При неизменном объеме газ не совершает механическую работу, и переданное ему извне тепло целиком превращается во внутреннюю энергию[17]:

Q_V=DU=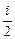nRDT (6.3.1)

Способность тела нагреваться при сообщении ему тепла характеризует теплоемкость. Различают удельную и молярную теплоемкости. Будем их обозначать соответственно строчной (маленькой) и прописной (заглавной) буквами: с и С. Напомним: Q=mcDT=nCDT. Из этих формул следует, что C=Mc. При разных процессах подвода тепла газ нагревается по-разному. Теплоемкость газа при конкретном процессе обозначают соответствующим индексом. Для молярной теплоемкости идеального газа при постоянном объеме получаем, используя формулу 6.3.1:

C_V =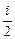R (6.3.2)

Анализируя формулу 6.3.2, видим, что молярная теплоемкость зависит от числа степеней свободы молекулы и одинакова для любых газов, молекулы которых содержат одинаковое число атомов. Экспериментальные исследования показали, что для газов, в частности, для молекулярного водорода (Н₂) при температурах не слишком низких или не слишком высоких по сравнению с обычными (10² К< T< 10³ K) эта формула дает хорошее согласие с опытом. При низких температурах теплоемкость двухатомного газа такова, как если бы его молекула имела не пять, а только три степени свободы, соответствующие ее поступательному движению. При высоких температурах у двухатомной молекулы появляются еще две степени свободы, т.е. кроме поступательного и вращательного у молекулы появляются дополнительные виды движения. Объяснение этому дает квантовая механика. Мы уже упоминали, что классическая модель идеального газа, как и всякая физическая модель, имеет определенную область применения, и реальный газ можно считать идеальным только при условиях, мало отличающихся от обычно встречающихся в природе.

Отметим еще раз, что внутренняя энергия является функцией состояния тела, и ее изменение одинаково для любых процессов, связывающих начальное и конечное состояния системы. В частности, как видно из рассмотренного, для идеального газа при любом процессе

DU=nC_VDT (6.3.3)

2. Изобарный процесс: р=const. Работа газа (см. формулы 6.2.3 и 5.3.2)

А=рDV=nRDT (6.3.4)

Изменение температуры газа при сообщении ему тепла Q_p зависит от теплоемкости газа при постоянном давлении С_р:

Q_p=n С_р DT (6.3.5)

Из формул 6.2.4, 6.3.3, 6.3.4 и 6.3.5 получаем:

С_р= C_V+R (6.3.6)

Этот результат имеет ясный физический смысл. При нагревании газа при постоянном объеме все тепло идет на увеличение внутренней энергии. При нагревании при постоянном давлении помимо этого тепло идет на совершение работы по расширению газа. В результате молярная теплоемкость идеального газа при постоянном давлении больше его молярной теплоемкости при постоянном объеме на величину газовой постоянной. Из формул 6.3.6 и 6.3.2 следует:

С_р=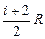 (6.3.7)

Отметим, что, зная число степеней свободы молекулы i и одну из величин Q, DU, A, остальные две нетрудно найти. Получите эти формулы самостоятельно.

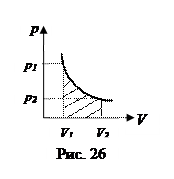3. Изотермический процесс: Т=const. В этом процессе внутренняя энергия не изменяется, и все переданное газу тепло идет на совершение работы: Q=A. Уравнение изотермического процесса pV = const, на pV - диаграмме его график - гипербола (рис. 26). Выведем формулу работы при изотермическом процессе, используя формулу (6.2.3) и уравнение Менделеева – Клапейрона:

A=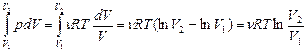 (6.3.8)

При изотермическом процессе DT =0 при сообщении телу любого количества тепла. Из определения теплоемкости следует, что C _T = ¥, поэтому иногда про изотермический процесс говорят как про процесс, происходящий с телом с бесконечной теплоемкостью.

4. Адиабатный процесс происходит в теплоизолированной системе, когда ни в нее, ни из нее не проникает тепло: Q= 0. Этот процесс называется еще изоэнтропийным [18]: S = const. Из первого начала термодинамики следует: DU+A= 0, и A= -DU. Работа газа при расширении положительная, при адиабатическом процессе она происходит за счет уменьшения его внутренней энергии. Это значит, что при адиабатном расширении газ охлаждается, а при адиабатном сжатии нагревается. Такие примеры хорошо известны из повседневной практики. Быстро протекающие процессы, когда не успевает происходить теплообмен с окружающей средой, приближаются к адиабатным. Вероятно, Вы замечали, что при накачивании насосом камеры велосипедной или автомобильной шины насос нагревается тем больше, чем быстрее Вы работаете. При накачивании воздух сжимается и нагревается, если не успевает происходить теплообмен. Процесс распространения звука в воздухе связан с быстрым расширением и сжатием малых объемов воздуха с частотой звуковых колебаний (несколько тысяч раз в секунду), и он приблизительно адиабатный.

Выведем уравнение адиабаты, связывающее параметры состояния газа при адиабатном процессе. Для него dA=-dU, т.е. pdV=-nC_VdT. Продифференцировав уравнение состояния, получаем:

pdV+Vdp=nRdT. Из двух последних уравнений следует: pdV+Vdp=-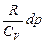 и далее:

(1+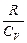) pdV+Vdp= 0. Учитывая, что , и обозначая

g =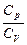= 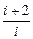(6.3.9)

перепишем предыдущее дифференциальное уравнение с разделяющимися переменными так: , проинтегрируем его: glnp+lnV=ln const и после потенцирования получим уравнение адиабатного процесса:

pV^g= const (6.3.10)

Это уравнение называют уравнением Пуассона. Пользуясь уравнением Клапейрона – Менделеева, уравнение адиабаты можно записать еще так[19]: TV^g-1= const или так: p ^{1 - g}T^g= const.

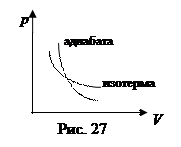
g - безразмерная величина, называется показателем адиабаты. Его значение больше единицы и зависит от числа степеней свободы молекулы (см. формулу 6.3.9). Сравнивая уравнение Пуассона с уравнением изотермы (pV= const) видим, что на pV - диаграмме график адиабаты похож на график изотермы, но более крутой (рис.27). Из рисунка видно, что при одинаковом расширении газа работа в изотермическом процессе больше, чем при адиабатном. При сжатии результат обратный (сравните площади под соответствующими графиками).

§ 6.4. Тепловая и холодильная машины

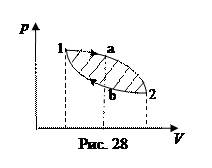1. Тепловая машина (двигатель) совершает механическую работу, превращая в нее тепло. Рабочим телом служит газ, заключенный в цилиндре двигателя. При сообщении газу тепла он расширяется, толкает поршень, и движение поршня приводит в движение, например, колеса автомобиля. Процесс совершения газом работы при переходе его из состояния 1 в состояние 2 представлен на рис. 28 графиком 1а2. Работа газа А_1а2 равна площади под графиком процесса на диаграмме. Для восстановления работоспособности двигателя поршень надо вернуть в исходное состояние, т.е. сжать газ. Если сжимать его процессом 2а1, то работа сжатия равна работе расширения, и после возвращения газа в состояние 1 суммарная работа обратится в ноль. Понятно, что сжимать газ надо другим путем, график которого идет ниже графика расширения. Тогда суммарная работа (она изображена на графике заштрихованной площадью) окажется положительной. Процесс, в результате которого тело после ряда изменений своего состояния возвращается в исходное состояние, называется круговым процессом или циклом. Понятно, что в тепловой машине используется цикл.

Отметим еще одно обстоятельство. На стадии расширения температура газа выше, чем на стадии сжатия. Действительно, из рис. 28 видно, что при одном и том же объеме давление газа при расширении больше, чем при сжатии. Согласно уравнению состояния, той же закономерности следуют температуры. Это означает, что газ получает тепло при более высокой температуре, нежели отдает, и источником тепла служит горячее тело, а приемником тепла – холодное тело.

Рассмотрим цикл с точки зрения первого начала термодинамики. На стадии расширения газ получает тепло Q ₁ и совершает положительную работу A _1a2, на стадии сжатия отдает тепло - Q ₂ и совершает отрицательную работу - A _2b1. Запишем для обоих процессов уравнения первого начала термодинамики: Q ₁= U₂-U₁+A_1a2

Дата добавления: 2014-01-06