
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Физические теории 4 страница
|
|
|
|
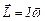 (4.5.1)
(4.5.1)
Момент импульса – аксиальный вектор, его единица в СИ обозначается (кг.м2/с). Основной закон динамики вращательного движения (4.4.2) констатирует, что момент импульса изменяется под действием момента силы, и это изменение пропорционально времени воздействия.
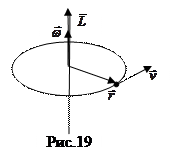 2. Рассмотрим тело как систему материальных точек, и воспользуемся соответствующим определением момента инерции (формула 4.1.1): L=Iw=Smiri2w =Smivi ri. Мы получили, что момент импульса а.т.т. равен сумме моментов м.т., образующих это тело. Момент импульса м.т. массы m, движущейся со скоростью v по окружности радиусом r равен:
2. Рассмотрим тело как систему материальных точек, и воспользуемся соответствующим определением момента инерции (формула 4.1.1): L=Iw=Smiri2w =Smivi ri. Мы получили, что момент импульса а.т.т. равен сумме моментов м.т., образующих это тело. Момент импульса м.т. массы m, движущейся со скоростью v по окружности радиусом r равен:
L=mvr (4.5.2)
На рис. 19 изображена такая точка: ось вращения лежит в плоскости рисунка, на рисунке указаны векторы 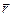 - положение точки на траектории,
- положение точки на траектории, 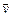 - ее скорость,
- ее скорость, 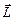 - момент импульса точки,
- момент импульса точки, 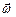 - угловая скорость тела. Вектор момента импульса м.т. определяется векторным произведением:
- угловая скорость тела. Вектор момента импульса м.т. определяется векторным произведением:
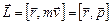 (4.5.3)
(4.5.3)
Напомним, 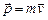 - импульс точки.
- импульс точки.
Момент импульса тела складывается из моментов импульсов всех его точек:
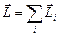 (4.5.4)
(4.5.4)
Отметим, что полученная нами формула (4.5.4) применима для определения момента импульса любой системы тел, а не только совокупности м.т., образующих а.т.т.
3. Рассмотрим систему тел. Каждое из них подчиняется основному закону динамики вращательного движения: 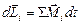 . Просуммируем эти формулы по всем телам системы. Напомним, что силы взаимодействия тел системы друг с другом и, соответственно, моменты этих сил, называются внутренними и, согласно третьему закону Ньютона, уравновешивают друг друга. В результате сложения получим в левой части уравнения изменение момента импульса системы, а в правой части сумму моментов внешних сил – их равнодействующую. Уравнение примет знакомую нам форму
. Просуммируем эти формулы по всем телам системы. Напомним, что силы взаимодействия тел системы друг с другом и, соответственно, моменты этих сил, называются внутренними и, согласно третьему закону Ньютона, уравновешивают друг друга. В результате сложения получим в левой части уравнения изменение момента импульса системы, а в правой части сумму моментов внешних сил – их равнодействующую. Уравнение примет знакомую нам форму 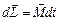 . В замкнутой системе тел
. В замкнутой системе тел 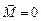 , поэтому изменение момента импульса
, поэтому изменение момента импульса 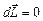 . Это проявление закона сохранения момента импульса: момент импульса замкнутой системы тел, равный векторной сумме моментов импульса всех ее частей, сохраняется:
. Это проявление закона сохранения момента импульса: момент импульса замкнутой системы тел, равный векторной сумме моментов импульса всех ее частей, сохраняется:
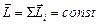 (4.5.5)
(4.5.5)
Есть много знакомых каждому из нас примеров проявления закона сохранения момента импульса: акробат выполняет сальто, балерина или фигурист выполняют пируэты, гироскоп (автопилот), опыты со скамьей Жуковского (вспомните лекционные демонстрации).
4. Приведенные выше рассуждения не следует считать выводом закона сохранения импульса, они разъясняют связь между разными законами, действующими в определенной физической системе. Применительно к системе материальных точек (§ 3.2), мы уже обсудили тот факт, что законы Ньютона и закон сохранения импульса – проявление одних и тех же свойств природы. Так и для системы вращающихся тел закон сохранения момента импульса и основной закон динамики вращательного движения взаимосвязаны. Напомним (см. § 3.1), что закон сохранения момента импульса называется фундаментальным, т.к. имеет самую широкую область применения (он «фундаментальнее» основного закона динамики вращательного движения) и есть следствие изотропности пространства.
§ 4.6. Краткие итоги главы 4
Обратим внимание на аналогию характеристик и формул законов динамики поступательного и вращательного движений, подчеркивающую общность их физического смысла. В частности, формулы поступательного движения превращаются в формулы вращательного движения (и, наоборот) при замене обозначений физических величин на их аналоги для другого вида движения.
| Характеристики и законы динамики | Вид движения | |
| Поступательное (м.т.) | Вращательное (а.т.т) | |
| Динамические характеристики | ||
| Мера инертности | m – масса | I - момент инерции |
| Мера внешнего воздействия | 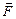 - сила - сила
| 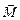 - момент силы - момент силы
|
| «Запас движения» | 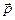 - импульс - импульс
| 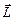 - момент импульса - момент импульса
|
| Формулы законов и определений | ||
| Уравнение движения | 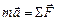 или или 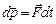
| 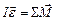 или или 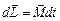
|
| Работа | 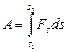
| 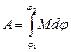
|
| Кинетическая энергия | 
| 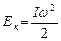
|
| Закон сохранения «запаса движения» замкнутой системы тел | 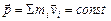
| 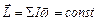
|
Раздел 2. Молекулярная физика и термодинамика
Глава 5. Кинетическая теория
§ 5.1. Тепловое движение
1. Вещество состоит из структурных элементов – атомов и молекул. Напомним, что массы атомов, измеренные в атомных единицах[6], указаны в таблице Менделеева. Массу молекулы вычисляют суммированием масс составляющих ее атомов. Эти массы называют относительной атомной, соответственно, относительной молекулярной массой. Даже микроскопическая с обыденной точки зрения масса вещества состоит из огромного числа частиц. Например, 1 см3 воздуха при обычных условиях имеет массу немного более 1 мг и содержит более 1019 частиц. В жидкостях и в твердых телах концентрация частиц еще больше, соответственно, больше плотность вещества. Макроскопическим считают тело, состоящее из такого числа частиц N, что ln N >>1[7].
Количество вещества принято измерять в молях. Моль – количество вещества, в котором содержится определенное число структурных единиц, оно называется числом (или постоянной) Авогадро: Na= 6,02.10 23 моль -1. Массу моля вещества называют молярной массой, ее численное значение в граммах равно относительной молекулярной массе. Для вещества в атомарном состоянии молярная масса численно равна атомной массе. Обозначим молярную массу М, массу одной молекулы т0, тогда
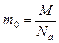 (5.1.1)
(5.1.1)
Совокупность частиц тела называют термодинамической системой. Термодинамической системой является любое макроскопическое тело: твердое, жидкое, газообразное.
2. Частицы (атомы и молекулы) вещества непрерывно хаотически движутся. Это движение называется тепловым. Именно оно определяет внутреннее состояние каждого тела и индивидуальные свойства вещества.
Фундаментальным свойством теплового движения является его «забывчивость». Поясним на примере. Капля окрашенной жидкости, попав в прозрачную воду, со временем равномерно распределится по всему объему. Окончательное состояние смеси будет одинаковым независимо от того, в каком месте в начальный момент появилась окрашенная капля - ее начальное состояние будет «забыто». Если внешние условия не изменяются, то равномерное распределение окрашенного вещества со временем меняться не будет. Не изменяющееся со временем состояние называется стационарным. В стационарном состоянии тела через его границы может переноситься не изменяющийся со временем поток вещества, энергии, импульса, электрического заряда. Например, при протекании тока по проводнику через его поперечное сечение происходит перенос заряда, а через поверхность проводника переносится энергия в виде количества тепла. Если через границы тела нет никаких потоков, то такое тело называется изолированной термодинамической системой. «Забывчивость» теплового движения приводит изолированную термодинамическую систему в состояние, которое называется тепловым или термодинамическим равновесием. В равновесном состоянии в любых участках системы характеристики одинаковы и неизменны.
Именно тепловое движение и его «забывчивость» являются причиной возникновения термодинамического равновесия.
3. Модель материального тела представляет собой систему огромного числа частиц. Каждая частица в зависимости от обстоятельств и рассматриваемого явления может быть представлена моделью классической, например, м.т. или а.т.т., или квантовой. Взаимодействие частиц друг с другом подчиняется известным законам (классическим или квантовым). Движение каждой отдельной частицы можно рассчитать, используя законы динамики. Действительно, зная начальное состояние всех частиц и законы их взаимодействия, можно для каждой из них составить и решить уравнение движения. Однако подумайте, какое громадное число уравнений надо решить и сколько для этого требуется времени, жизни не хватит! Если даже эти уравнения будут решены, то полученная из них информация окажется бесполезной: при термодинамическом равновесии состояние системы остается неизменным, тогда как состояние каждой частицы непрерывно изменяется в результате ее теплового движения. Это значит, что одному и тому же состоянию всей системы (его называют макросостоянием) соответствует множество разных состояний частиц системы (микросостояний).
Предметом изучения молекулярной физики и термодинамики являются свойства и поведение термодинамической системы как целого. Из сказанного ясно, что динамическое описание системы многих частиц неосуществимо с технической, непригодно с теоретической и бесполезно с практической точек зрения.
4. Для изучения свойств макротел (термодинамических систем) физика использует два метода: статистический и термодинамический.
Статистический метод основан на теории вероятностей и истолковывает свойства тел как суммарный, усредненный результат движения отдельных молекул. Статистический метод выявляет закономерности, которым подчиняется, казалось бы, полный беспорядок в движении отдельных молекул.
Термодинамический метод является феноменологическим[8]. Это означает, что он рассматривает тело «снаружи», не вдаваясь в его внутреннее строение, на основе небольшого числа фундаментальных законов (они называются началами термодинамики), полученных обобщением опыта. Термодинамический метод иногда называют энергетическим методом рассмотрения тел (первое начало термодинамики – закон сохранения энергии). Этот метод широко применяется при анализе различных физических систем и явлений, изучаемых в разных разделах физики.
Статистический и термодинамический методы взаимно дополняют друг друга, образуя, по сути, единое целое.
§ 5.2. Основное уравнение кинетической теории газа
1. Атомы и молекулы вещества на небольших по сравнению с их размерами расстояниях притягиваются друг к другу, причем, силы притяжения быстро уменьшаются при увеличении расстояния. В газах его частицы большую часть времени находятся так далеко друг от друга, что силы притяжения не в состоянии противодействовать разбрасывающему их тепловому движению. При сближении частиц на расстояния, соответствующие столкновению, силы притяжения частиц сменяются силами отталкивания, и частицы вновь разлетаются. Можно считать, что между столкновениями частицы движутся свободно, при этом время свободного движения значительно превосходит время столкновений, и газ вследствие теплового движения всегда полностью занимает предоставленный ему объем. Отсюда модель идеального газа:
· собственный объем молекул мал по сравнению с объемом газа (т.е.с объемом сосуда):
· потенциальная энергия взаимодействия молекул пренебрежимо мала по сравнению с кинетической энергией хаотического движения, так что можно считать, что между двумя последовательными столкновениями частицы движутся свободно, т.е. равномерно и прямолинейно;
· вследствие хаотичности любые направления движения частиц равновероятны, т.е. в любом направлении в любой момент времени движется примерно одинаковое число частиц;
· соударения молекул друг с другом и со стенками сосуда упругие.
2. При столкновении со стенкой сосуда молекула сообщает ей импульс. Напомним, что переданный в единицу времени импульс равен силе, действующей на стенку, а сила, направленная перпендикулярно к поверхности, и отнесенная к единице площади поверхности, равна давлению: 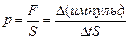 . Для простоты рассмотрим сосуд прямоугольной формы объемом V=Sl, где S – площадь боковой стенки, перпендикулярной оси х, l - длина ребра вдоль оси х (см. рис. 20). Одна из молекул (ее масса m 0) летит вдоль оси х со скоростью υ из точки 1, в точке 2 упруго сталкивается со стенкой, сообщает ей импульс 2 m 0 υ и отскакивает без потери скорости к противоположной стенке. Ударившись в точке 1, молекула опять движется в точку 2 и, спустя время
. Для простоты рассмотрим сосуд прямоугольной формы объемом V=Sl, где S – площадь боковой стенки, перпендикулярной оси х, l - длина ребра вдоль оси х (см. рис. 20). Одна из молекул (ее масса m 0) летит вдоль оси х со скоростью υ из точки 1, в точке 2 упруго сталкивается со стенкой, сообщает ей импульс 2 m 0 υ и отскакивает без потери скорости к противоположной стенке. Ударившись в точке 1, молекула опять движется в точку 2 и, спустя время 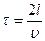 опять сообщит стенке такой же
опять сообщит стенке такой же 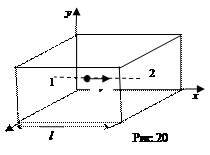 импульс. За единицу времени этот процесс произойдет 1/ t раз, так что удары одной молекулы о стенку сосуда создадут силу m 0 υ 2/l.
импульс. За единицу времени этот процесс произойдет 1/ t раз, так что удары одной молекулы о стенку сосуда создадут силу m 0 υ 2/l.
Учитывая, что в сосуде N молекул, и их направления движения равновероятны, без потери общности рассуждений можем предположить, что вдоль оси х движется 1/3 всех молекул, и их общая сила давления на стенку равна 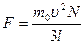 . Давление
. Давление 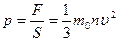 , где
, где 
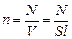 - концентрация молекул, т.е. их число в единице объема. Учтем, что скорости движения молекул различны, и вклад каждой молекулы в давление пропорционален квадрату ее скорости, тогда
- концентрация молекул, т.е. их число в единице объема. Учтем, что скорости движения молекул различны, и вклад каждой молекулы в давление пропорционален квадрату ее скорости, тогда
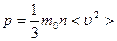 (5.2.1)
(5.2.1)
Здесь < υ 2> - среднее значение квадрата скорости, оно равно сумме квадратов скоростей всех молекул, деленной на их число. Эта величина также называется квадратом средней квадратичной скорости: 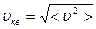 . Формула (5.2.1) выражает уравнение молекулярно-кинетической теории давления газа. Она показывает, что давление газа – статистический параметр, и равно среднему импульсу, переданному единице площади стенки сосуда в единицу времени при столкновении с ней молекул вследствие их теплового движения. Заметим, что газ, находящийся в состоянии термодинамического равновесия, такое давление будет оказывать на все стенки сосуда любой формы.
. Формула (5.2.1) выражает уравнение молекулярно-кинетической теории давления газа. Она показывает, что давление газа – статистический параметр, и равно среднему импульсу, переданному единице площади стенки сосуда в единицу времени при столкновении с ней молекул вследствие их теплового движения. Заметим, что газ, находящийся в состоянии термодинамического равновесия, такое давление будет оказывать на все стенки сосуда любой формы.
3. В рассмотренной модели идеального газа молекулы считаются материальными точками. Кинетическая энергия теплового движения 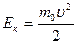 у разных молекул разная вследствие различия скоростей хаотического движения. Усредним ее по всем молекулам. и назовем средней кинетической энергией поступательного хаотического движения молекул <Eпост>. Она выражается формулой:
у разных молекул разная вследствие различия скоростей хаотического движения. Усредним ее по всем молекулам. и назовем средней кинетической энергией поступательного хаотического движения молекул <Eпост>. Она выражается формулой:
<Eпост> =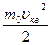 (5.2.2)
(5.2.2)
Основное уравнение кинетической теории газа можно записать еще и так:
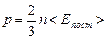 (5.2.3)
(5.2.3)
Уравнение (5.2.3) констатирует, что давление идеального газа зависит от концентрации молекул и их средней энергии поступательного движения. Формулы основного уравнения кинетической теории (5.2.1) и (5.2.3) связывают между собой величины, усредненные по всем молекулам: p, n, <Eпост>. Эти величины характеризуют не отдельную молекулу, а всю рассматриваемую термодинамическую систему – газ и являются характеристиками (параметрами) состояния газа. Таким образом, основное уравнение кинетической теории идеального газа является уравнением состояния идеального газа.
§ 5.3. Уравнение Клапейрона – Менделеева
1. Экспериментальное изучение поведения газов в XVII – XIX веках показало, что состояние газа определяют давление p, объем V и температура Т. Напомним, что температура характеризует степень нагретости тела. Абсолютная температура Т не бываем отрицательной, измеряется в кельвинах (К) и связана с температурой t, измеренной в градусах Цельсия так:
T = (t 0C + 273)К (5.3.1)
p, V и Т называются параметрами (или термодинамическими параметрами) состояния газа, и они взаимосвязаны друг с другом. Уравнение, связывающее между собой параметры состояния, называется уравнением состояния. Оно было получено из опытных газовых законов Бойля-Мариотта, Гей-Люссака и Шарля и называется уравнением Клапейрона – Менделеева или уравнением состояния идеального [9] газа:
рV=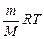 (5.3.2)
(5.3.2)
Здесь m – масса газа, M – молярная масса, R – универсальная (или молярная) газовая постоянная, в СИ R = 8,3 Дж/(моль.К). Напомним, что количество вещества 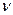 в СИ измеряют в моль, оно выражается так:
в СИ измеряют в моль, оно выражается так:
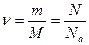 (5.3.3)
(5.3.3)
2. Используя понятие концентрации частиц и постоянную Больцмана
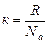 , (к = 1,38.10-23 Дж/К) (5.3.4)
, (к = 1,38.10-23 Дж/К) (5.3.4)
получаем еще одну формулу уравнения состояния газа:
р=пкТ (5.3.5)
Уравнение состояния содержит в себе, в частности, закон Авогадро, полученный из опыта. Он гласит, что при одинаковых температурах и одинаковых давлениях в одинаковых объемах любых газов содержится одинаковое число частиц. И это же уравнение содержит в себе опытный факт: при нормальных условиях [10] один моль любого газа занимает объем V= 22,4 л. (Вспомните, сколько структурных единиц в 1 моль и оцените, сколько молекул в воздухе того помещения, где Вы сейчас находитесь).
§ 5.4. Молекулярно-кинетический смысл абсолютной температуры. Средняя энергия теплового движения молекулы
1. Сравним уравнения состояния газа в форме (5.2.3) и в форме (5.3.5). Первое из них получено теоретически в модели идеального газа, второе есть обобщение опыта. Сравнение этих формул раскрывает смысл абсолютной температуры как меры средней энергии теплового движения молекул: 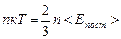 . Чаще эту формулу записывают так:
. Чаще эту формулу записывают так:
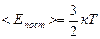 (5.4.1)
(5.4.1)
Формула (5.4.1) показывает, что абсолютная температура Т является статистической характеристикой. Понятие температуры не применимо к одной частице (молекуле) вещества. Оно имеет физический смысл только для равновесного состояния термодинамической системы, и является термодинамическим параметром состояния. В состоянии термодинамического равновесия средняя энергия теплового движения молекул разных газов одинакова при одинаковых температурах. Это означает, что в смеси газов, например, в воздухе, тяжелые частицы, например, молекулы кислорода, движутся в среднем медленнее легких молекул водорода.
Из приведенных рассуждений следует еще один важный вывод: модель идеального газа применима к реальному газу, подчиняющемуся опытным газовым законам, другими словами, идеальный газ - это реальный газ, подчиняющийся уравнению Клапейрона - Менделеева.
2. Напомним, что число независимых координат, однозначно задающих положение тела в пространстве, называют числом степеней свободы и обозначают i. Одноатомные молекулы в модели идеального газа считаются материальными точкам, для них i= 3. Это означает, что произвольное движение м.т. в пространстве можно рассматривать как сумму движений по трем осям координат одновременно. При поступательном движении твердого тела все его точки движутся одинаково, так что любое движение одноатомной молекулы, как и поступательное движение а.т.т., имеет три степени свободы поступательного движения: iпост = 3. Кинетическая энергия Е к= mυ2/ 2= m (υx2+υy2+υz2)/2 также является суммой трех слагаемых. Вследствие хаотичности движения средние значения квадратов проекций скоростей на все три оси координат одинаковы, и на каждую степень свободы поступательного движения приходится одинаковая энергия кТ /2. Формулу (5.4.1) можно записать так:
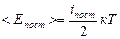 (5.4.2)
(5.4.2)
Из одноатомных молекул состоят инертные газы (He, Ne). Молекулы других газов (H2, O2, CO2, CH4 - метан) состоят из двух-, трех-, многоатомных молекул. Эти газы подчиняются уравнению Клапейрона – Менделеева, и тоже являются идеальными. В модели идеального газа их молекулы являются абсолютно твердыми телами, состоящими из двух, трех и более материальных точек (атомов). Твердое тело может двигаться поступательно и вращаться. Его число степеней свободы складывается из числа степеней свободы поступательного и вращательного движений:
i = iпост + iвр ащ (5.4.3)
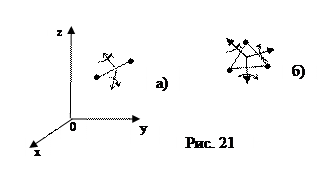 На рис. 21 показаны двухатомная и трехатомная молекулы. Положение двухатомной молекулы задают пять координат. Каждая точка (атом) имеет три координаты, и эти шесть чисел связаны между собой уравнением, выражающим неизменное расстояние между точками. Зная пять координат, шестую можно вычислить из этого уравнения. Таким образом, двухатомная молекула имеет пять степеней свободы. Рассуждая аналогичным образом, получаем, что число степеней свободы трехатомной молекула равно шести. Напомним, что моделью многоатомной молекулы служит а.т.т., положение которого в пространстве однозначно задают три точки, не лежащие на одной прямой. Следовательно, число степеней свободы жесткой молекулы, состоящей из трех и более атомов, равно шести.
На рис. 21 показаны двухатомная и трехатомная молекулы. Положение двухатомной молекулы задают пять координат. Каждая точка (атом) имеет три координаты, и эти шесть чисел связаны между собой уравнением, выражающим неизменное расстояние между точками. Зная пять координат, шестую можно вычислить из этого уравнения. Таким образом, двухатомная молекула имеет пять степеней свободы. Рассуждая аналогичным образом, получаем, что число степеней свободы трехатомной молекула равно шести. Напомним, что моделью многоатомной молекулы служит а.т.т., положение которого в пространстве однозначно задают три точки, не лежащие на одной прямой. Следовательно, число степеней свободы жесткой молекулы, состоящей из трех и более атомов, равно шести.
Любое движение молекулы, перемещающее ее в новое положение в пространстве, можно разделить на два: поступательное, задаваемое перемещением ее центра инерции по осям x, y и z, и вращательное вокруг других трех осей координат, жестко связанных с центром инерции. Эти оси координат показаны на рисунке, там же стрелками указаны возможные направления вращений, дающие новое положение молекулы. Итак, для любой молекулы iпост =3. Для двухатомной молекулы iвр ащ =2, для трех-, многоатомной молекулы iвр ащ =3 (см. формулу 5.4.3).
3. При столкновениях друг с другом молекулы обмениваются энергией. В результате удара поступательно движущаяся многоатомная молекула может начать вращаться, или, наоборот, вращающаяся молекула может начать двигаться поступательно. В общем случае кинетические энергии поступательного и вращательного движений при тепловом движении молекул газа изменяются хаотически. Эти соображения составляют суть теоремы о равном распределении энергии по степеням свободы (приводим ее без вывода): на каждую степень свободы теплового движения частицы приходится одинаковая средняя кинетическая энергия, равная  .
.
Средняя энергия теплового движения молекулы с учетом всех ее степеней свободы выражается формулой:
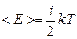 (5.4.3)
(5.4.3)
Еще раз отметим, что в модели идеального газа молекулы жесткие (а.т.т) и имеют только поступательные и вращательные степени свободы. Эта модель дает хорошее согласие с опытом при температурах, не слишком низких, или, наоборот, не слишком высоких. Этому диапазону соответствуют температуры (102 …103) К. При низких температурах «заморожены», т.е. отсутствуют вращательные степени свободы. При высоких температурах молекулы перестают быть жесткими, атомы в них колеблются, возбуждаются колебательные степени свободы. В этих температурных областях проявляются квантовые свойства движения, и классическая теория не работает.
§ 5.5. Распределение Максвелла молекул газа по скоростям
1. Тепловое движение молекул приводит к установлению равновесного состояния изолированной термодинамической системы, а это означает, что в хаосе есть определенная закономерность. Поясним это на следующем примере. Будем ежедневно в течение 40 минут наблюдать приход сотрудников и студентов к началу рабочего дня, считая, сколько человек приходят ежеминутно. Мы увидим, что по мере приближения звонка поток вначале нарастает, достигает максимума, и начинает снижаться в последние перед звонком минуты. Время прихода конкретных людей, особенно тех, кто вынужден пользоваться транспортом, день ото дня может изменяться случайным образом, тогда как общая закономерность зависимости потока людей от оставшегося до звонка времени сохраняется.
Обратимся к тепловому движению молекул газа в равновесном состоянии. Предположим, что в каждый момент времени мы знаем величины скоростей всех N молекул. Весь диапазон значений скоростей разделим на равные промежутки шириной Dυ, посчитаем для каждого промежутка число молекул DN, чья скорость попала в этот промежуток, и найдем долю этих молекул: 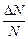 . В следующий момент времени хаотическое движение может переместить любую конкретную молекулу в другой промежуток скоростей, однако доля молекул в каждом из рассматриваемых промежутков практически не изменится: на место ушедшей приходит другая. При тепловом движении молекулы просто обмениваются местами в ряду скоростей, а число мест в каждом конкретном промежутке скоростей сохраняется. Доля, или частота определенных случайных событий, характеризует их вероятность. По определению вероятность есть
. В следующий момент времени хаотическое движение может переместить любую конкретную молекулу в другой промежуток скоростей, однако доля молекул в каждом из рассматриваемых промежутков практически не изменится: на место ушедшей приходит другая. При тепловом движении молекулы просто обмениваются местами в ряду скоростей, а число мест в каждом конкретном промежутке скоростей сохраняется. Доля, или частота определенных случайных событий, характеризует их вероятность. По определению вероятность есть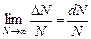 [11]. Функция f (υ)=
[11]. Функция f (υ)=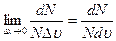 называется плотностью вероятности. Она показывает вероятность того, что, измерив в данный момент времени скорость выбранной наугад молекулы газа, получим значение υ. Наши рассуждения свидетельствуют, что скорости молекул изменяются хаотически, а вероятность того, что в любой момент времени скорость случайным образом выбранной молекулы окажется равной конкретной величине υ, имеет свое неизменное значение. Действительно, в хаосе действует определенная статистическая закономерность. Эта теоретическая закономерность была получена Максвеллом и называется распределением молекул газа по скоростям. Она выражается формулой:
называется плотностью вероятности. Она показывает вероятность того, что, измерив в данный момент времени скорость выбранной наугад молекулы газа, получим значение υ. Наши рассуждения свидетельствуют, что скорости молекул изменяются хаотически, а вероятность того, что в любой момент времени скорость случайным образом выбранной молекулы окажется равной конкретной величине υ, имеет свое неизменное значение. Действительно, в хаосе действует определенная статистическая закономерность. Эта теоретическая закономерность была получена Максвеллом и называется распределением молекул газа по скоростям. Она выражается формулой:
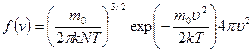 (5.5.1)
(5.5.1)
Формула (5.5.1) содержит два сомножителя, зависящих от величины скорости. Первый сомножитель – квадратичная функция (парабола) растет с увеличением скорости, второй – экспоненциальная с отрицательным показателем степени, наоборот, уменьшается. При υ= 0 е0=1, и для очень малых скоростей величина второго сомножителя мало отличается от 1, так что f (υ)~ υ 2. В итоге функция распределения вначале растет при возрастании скорости от нулевого значения. Для больших скоростей (υ ® ¥, e-¥®0) рост параболы не может противостоять резкому спаду экспоненты, и f (υ) ®0. Следовательно, при некотором значении скорости функция распределения достигает максимума. Это значение скорости υ вер называется наиболее вероятным, ему соответствует максимум вероятности. А это значит, что чаще всего нам будут попадаться молекулы, скорости которых близки к наиболее вероятной. Исследовав функцию распределения (5.5.1) на максимум, получим формулу:
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 387; Нарушение авторских прав?; Мы поможем в написании вашей работы!