Физические теории 7 страница

Рис. 34

Диполь – два точечных разноименных зарядов одинаковой величины. На рис. 34 в одной из точек поля диполя показано построение вектора напряженности с помощью принципа суперпозиции. Силовые линии – воображаемые, но их можно сделать видимыми (вспомните лекционные демонстрации).

§ 7.3. Теорема Гаусса.

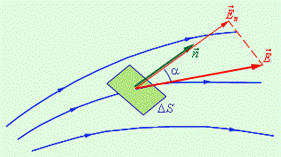1. Принцип суперпозиции позволяет рассчитать электрическое поле, созданное любыми заряженными телами, рассматривая их как систему точечных зарядов. Иногда это сопряжено с заметными математическими трудностями. Поле, созданное симметричным распределением зарядов, значительно легче рассчитать, используя теорему Гаусса. Ее формулировка использует понятие потока вектора напряженности через поверхность. Поток вектора – скалярная величина, он равен числу силовых линий, пересекающих эту поверхность. На рис. 35 силовыми линиями изображено электростатическое поле, в котором находится плоская поверхность площадью DS. Ее пространственную ориентацию указывает нормаль , образующая с угол a. Поток через эту элементарную поверхность равен EDScosa. = E_nDS. Из определения ясно, что поток положительный, если 0£ a < 90⁰ (силовые линии входят в поверхность); поток отрицательный, если 90⁰£ a <180⁰ (силовые линии выходят из поверхности); поток равен нулю, если a =90⁰ (силовые линии скользят по поверхности, не пересекая ее).

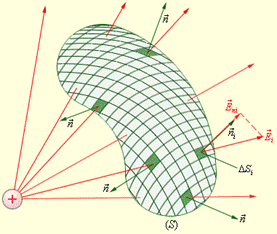Теперь найдем поток через замкнутую поверхность произвольной формы (рис.36). Разобьем эту поверхность на элементарные участки площадью dS (на рисунке они обозначены DS), найдем элементарные потоки и просуммируем их по всей поверхности. Заметим, что в любой точке замкнутой поверхности нормаль принято направлять наружу. Поток через замкнутую поверхность обозначают так: 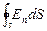. Кружок на интеграле указывает, что поверхность замкнутая. Заметим, что на нашем рисунке поток равен нулю: число входящих в поверхность силовых линий равно числу выходящих из нее, линии насквозь проходят через поверхность. Вспомним, что силовые линии электрического поля начинаются и заканчиваются на зарядах, т.е. источниками и стоками потока являются заряды. Понятно, что если внутри замкнутой Рис 36 поверхности нет зарядов, то поток через нее равен нулю. Поток – это разность числа входящих в поверхность и выходящих из нее силовых линий. Мысленно деформируйте или переместите на новое место поверхность на рис. 36. Поток через нее всегда равен нулю, если заряд находится снаружи. Если заряд окажется внутри, то поток через поверхность любого размера и формы один и тот же. Это и есть содержание теоремы Гаусса: поток вектора напряженности электростатического поля в вакууме через любую замкнутую поверхность равен алгебраической сумме зарядов, заключенных внутри этой поверхности, деленной на электрическую постоянную:

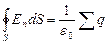(7.3.1)

2. Рассмотрим примеры применения теоремы Гаусса.

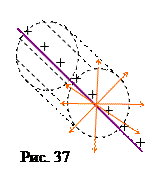а) Поле однородно заряженной бесконечной нити. На рис. 37 показан отрезок нити (фиолетовая линия), на нити равномерно распределен заряд (его обозначили знаками «плюс»). На каждом элементе длины dl содержится заряд dq, линейная плотность заряда t = dq/dl= const. Понятно, что поле обладает цилиндрической симметрией. Это значит, что линии напряженности (оранжевые векторы) направлены по радиусам прямого цилиндра, ось которого совпадает с нитью. В качестве замкнутой поверхности рассмотрим часть такого прямого цилиндра радиусом r и длиной l, на рисунке он показан пунктирными линиями. Силовые линии пересекают боковую поверхность цилиндра по нормали, создавая поток ES _бок= E 2p rl, и скользят вдоль оснований цилиндра, не создавая потока сквозь них. Суммарный заряд, заключенный внутри этой поверхности q=tl. Подставляя эти результаты в формулу (7.3.1), получаем:

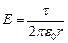(7.3.2)

б) Бесконечная однородно заряженная плоскость. Поверхностная плотность заряда s=dq/dS= const. Из соображений симметрии ясно, что силовые линии равномерно выходят из плоскости перпендикулярно к ней в обе стороны, если плоскость заряжена положительно, и входят в нее, если заряд плоскости отрицательный. (Сделайте рисунок самостоятельно). С каждой стороны плоскости линии напряженности направлены в противоположные стороны, но густота их одинакова. В качестве замкнутой поверхности выберем поверхность прямого цилиндра, образующие которого перпендикулярны заряженной плоскости, а основания параллельны ей. Силовые линии скользят по его боковой поверхности и пересекают оба основания параллельно нормали к каждому основанию. Суммарный поток равен 2 ES. Суммарный заряд, находящийся внутри поверхности, q=ES. Из теоремы Гаусса получаем:

E=s /2 e₀ (7.3.3)

в) Плоский конденсатор. Он образован двумя бесконечными разноименно заряженными плоскостями с одинаковой плотностью зарядов: s ₊= s_- = s = const (рис. 38). 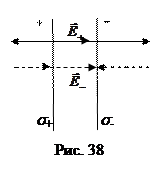На рисунке обозначены заряды плоскостей и нарисовано по одной силовой линии полей этих зарядов. Согласно принципу суперпозиции 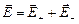, так что

E=s / e₀ , внутри конденсатора (7.3.4)

Е= 0, снаружи конденсатора (7.3.5)

Плоский конденсатор является источником однородного электрического поля, во всех точках которого векторы напряженности одинаковы, а силовые линии – параллельные прямые, проведенные с равномерной плотностью, при этом поле сосредоточено в пространстве между пластинами. Разумеется, реальный плоский конденсатор имеет пластины конечных размеров, и вблизи его краев поле неоднородное. Но чем меньше разница между расстоянием между пластинами и линейным размером пластин, тем точнее электростатическое поле в центральной части объема конденсатора соответствует однородному. На практике для получения однородного поля используют плоский конденсатор.

г) Поле равномерно заряженной сферы. Из соображений симметрии ясно, что силовые линии – радиальные прямые[23]. Такое поле называется сферически симметричным. Легко посчитать поток через любую сферическую поверхность радиуса r, центр которой совпадает с центром заряженной сферы: 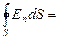ES=E 4p r². Если радиус поверхности интегрирования равен или больше радиуса сферы R (r ³ R), то находящийся внутри поверхности интегрирования заряд равен заряду сферы q. Если r < R, то внутри поверхности интегрирования нет заряда. Применяя теорему Гаусса, получаем: равномерно заряженная сфера снаружи создает такое же поле, как точечный заряд, помещенный в ее центр (см. формулы 7.2.2 и 7.2.3); внутри сферы поля нет, Е=0.

§ 7.4. Потенциал и работа электростатического поля.

1. Кулоновские силы консервативные, а их поле потенциальное. Напомним, что консервативными называются силы, работа которых одинакова для любых траекторий, соединяющих две точки. Работа консервативной силы по любому замкнутому пути равна нулю. Представим себе, что в электростатическом поле находится «чужой» заряд. На него действует кулоновская сила. Пусть этот заряд переместился по замкнутой траектории и вернулся в исходную точку. Источники электростатического поля неподвижны. После возвращения «чужого» заряда в исходное положение никаких изменений в системе не останется, все заряды окажутся в исходном положении. В соответствии с законом сохранения энергия системы не может измениться, и работа сил должна быть равна нулю. Следовательно, электростатическое поле потенциальное, и «чужой» заряд q в каждой точке поля имеет определенное значение потенциальной энергии W_п [24]. Работа по перемещению заряда q из точки 1 в точку 2 равна убыли его потенциальной энергии: А₁₂=W_п1-W_п2. С другой стороны, А₁₂=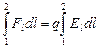. Здесь dl – элементарное перемещение заряда q. Сравнивая две эти две формул работы, получаем:

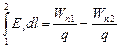(7.4.1)

2. Левая часть формулы (7.4.1) не зависит от величины заряда q, а определяется только полем, следовательно, и в правой части формулы стоит разность характеристик поля в двух его точках 1 и 2. Эту характеристику называют потенциалом электростатического поля в точке и обозначают j:

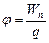(7.4.2)

Потенциал электростатического поля есть его энергетическая характеристика, он численно равен потенциальной энергии положительного единичного заряда, помещенного в данную точку. Единицу измерения потенциала в СИ называют вольт (В): 1В=1Дж/1Кл. Потенциальная энергия заряда q, находящегося в точке поля с потенциалом j

W_п=qj (7.4.3)

Работа электростатического поля по перемещению заряда из точки 1 в точку 2

А₁₂= q (j ₁ - j ₂) (7.4.4)

3. Формула (7.4.4) позволяет дать еще одно определение потенциала. Пусть точка 2 находится за пределами электростатического поля (т.е. бесконечно далеко от создавших его зарядов). Тогда j ₂=0, и потенциал в точке 1 поля численно равен работе по перемещению положительного единичного заряда из этой точки на бесконечность. Обозначим А_¥ - работу поля при перемещении «чужого» заряда q из точки поля с потенциалом j на бесконечность, тогда

j= А_¥ /q (7.4.5)

§ 7.5. Связь напряженности и потенциала электростатического поля.

1. Напряженность есть силовая характеристика поля в точке, потенциал – его энергетическая характеристика. Они связаны друг с другом подобно тому, как связаны друг с другом консервативная сила, действующая на частицу, и потенциальная энергия частицы. Работа поля по перемещению заряда q на элементарном пути dl может быть вычислена так: dA=qE_ldl=-qdj, откуда получаем:

E_l = -dj /dl (7.4.6)

Эта формула означает, что проекция 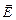на направление dl. равна производной со знаком «минус» от j по l. Если известен потенциал в каждой точке поля как функция координат j = j (х,у,z), то можно найти проекцию вектора напряженности на оси координат, а затем и вектор напряженности:

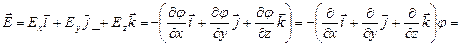-grad j (7.4.7)[25]

Из формулы (7.4.6), равно как из формул (7.4.1) и (7.4.2) следует:

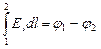(7.4.8)

Если перемещение происходит по замкнутому контуру, т.е. начальная точка 1 и конечная точка 2 пути совпадают, то криволинейный интеграл называют циркуляцией вектора по контуру и обозначают кружком на интеграле. Итак, в электростатическом поле циркуляция вектора напряженности по любому замкнутому контуру равна нулю:

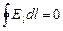(7.4.9)

Формула (7.4.9) математически выражает потенциальный характер поля.

2. Воспользуемся формулой (7.4.8) и получим формулу потенциала поля точечного заряда из формулы напряженности (см. формулы 7.2.2 и 7.2.3). Перемещение dl выберем вдоль направления вектора напряженности (dl= dr), тогда E_l=E=q/ (4p e₀r²). Положения точек 1 и 2 задано соответственно r₁ и r₂. 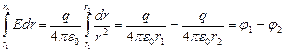. Получили формулу потенциала поля точечного заряда:

j =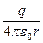 (7.4.10)

Используя принцип суперпозиции и учитывая, что потенциал – скаляр, получаем, что потенциал поля, созданного несколькими источниками, равен алгебраической сумме потенциалов, созданных в этой точке каждым источником независимо от всех прочих:

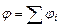(7.4.11)

3. Реальная или воображаемая поверхность в электрическом поле, все точки которой имеют одинаковый потенциал, называется эквипотенциальной поверхностью. Из формулы (7.4.8) видно, что эквипотенциальные поверхности поля точечного заряда – концентрические сферы, в центре которых находится источник поля. Обратите внимание, что силовые линии поля точечного заряда направлены радиально и перпендикулярны эквипотенциальным поверхностям. Убедитесь самостоятельно, что этот вывод справедлив для любого электростатического поля[26]. Сечение эквипотенциальных поверхностей плоскостью дает эквипотенциальные линии (эквипотенциали).

Электростатическое поле можно изображать не только линиями напряженности, но и эквипотенциальными поверхностями или эквипотенциальными линиями. На рис. 39 представлены три электростатических поля: точечного заряда, диполя и двух одинаковых положительных заряда. Эквипотенциали - синие линии, силовые линии – красные.

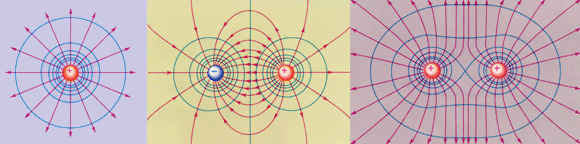Рис. 39

Эквипотенциали нарисованы с постоянным шагом Dj. Обратите внимание, что они, как и линии напряженности, сгущаются в области сильного поля. Вспомните, как на плоской топографической карте изображают рельеф местности, в частности, горы и возвышенности. На практике, исследуя топографию электростатического поля, легче измерить потенциалы (скаляр - одно число) разных точек поля, чем векторы напряженности (три числа), а затем, нарисовав эквипотенциали, построить линии напряженности (с таким способом Вы встретились в лабораторной работе N 22).

§ 7.6.Электростатическое поле в веществе.

1. Атомы вещества состоят из электронов и положительных ядер, и вещество в обычном состоянии электрически нейтрально. Однако под действием внешнего электрического поля 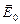его положительные и отрицательные заряды смещаются в противоположные стороны и создают свое собственное электрическое поле 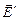. Поле в веществе 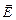=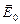+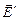отличается от поля в вакууме 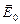. С точки зрения электрических свойств интересны два резко различающиеся класса веществ: диэлектрики (изоляторы) и проводники.

2. Диэлектрики используют для электрической изоляции проводящих тел друг от друга. В диэлектриках заряды под действием внешнего электрического поля 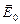смещаются в пределах атома и называются связанными. Созданное ими собственное поле направлено навстречу внешнему полю, так что напряженность поля в диэлектрике Е уменьшается по сравнению с Е₀. На рис.40 показан однородный неполярный диэлектрик. В неполярном диэлектрике в отсутствии внешнего электрического поля «центры тяжести» положительного и отрицательного зарядов молекулы совпадают, и ее дипольный момент равен нулю.

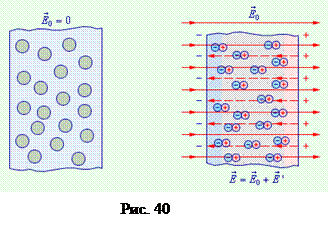Внешнее электрическое поле 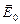(силовые линии сплошные) смещает эти «центры тяжести» в противоположные стороны. Каждая молекула превращается в электрический диполь. Внутри диэлектрика суммарный заряд всех диполей равен нулю, а на его противоположных поверхностях в тонком слое возникают нескомпенсированные разноименные связанные заряды (см. рис.40). Это явление называется поляризацией диэлектрика. Поляризованный диэлектрик создает собственное электростатическое поле 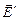(силовые линии штриховые), направленное навстречу 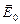. В диэлектриках другого типа (полярных, кристаллических) механизм поляризации носит другой характер. Однако возникшее в результате поляризации собственное поле 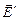все равно направлено навстречу внешнему полю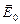. Густота силовых линий в диэлектрике уменьшается по сравнению с вакуумом. Относительная диэлектрическая проницаемость диэлектрика показывает, во сколько раз уменьшается поле в диэлектрике по сравнению с полем в вакууме, созданное одними и теми же внешними источниками:

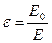(7.6.1)

Для многих однородных диэлектриков (кроме сегнетоэлектриков) ее значение не зависит от величины внешнего поля, и его можно найти в соответствующих таблицах физических свойств веществ. Заметим, что e₀E₀=e₀eE. Эту величину обозначают D, называют электрическим смещением или электрической индукцией. Это еще одна вспомогательная векторная характеристика электрического поля: в однородном диэлектрике

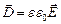(7.6.2)

Напряженность – силовая (физическая) характеристика поля. Она определяется как внешними, так и внутренними зарядами по отношению к диэлектрику. Электрическое смешение – вспомогательная (геометрическая) характеристика, связанная только с внешними по отношению к диэлектрику зарядами. Из формул (7.6.1) и (7.6.2) следует, что формулы для электростатического поля в вакууме становятся пригодными для поля в диэлектрике, если в них e₀ поменять на e₀e.

3. В проводниках имеются заряженные частицы, способные под действием сколь угодно малого электрического поля перемещаться в пределах объема тела. Такие заряды называются свободными. Хорошими проводниками являются металлы, например, медь, алюминий, серебро и другие, образованы из элементов первой и второй групп таблицы Менделеева. Их атомы в свободном состоянии имеют соответственно один или два валентных электрона. Взаимодействие атомов в металле приводит к тому, что валентные электроны покидают свой атом, становятся свободными и образуют своеобразный «электронный газ». Положительно заряженные ионы, получившиеся из атомов, образуют кристаллическую решетку, погруженную в электронный газ. В отсутствие внешнего электрического поля тепловое движение свободных электронов равномерно распределяет их по объему проводника. В результате в любой части объема проводника суммарный заряд равен нулю: положительный заряд кристаллической решетки и отрицательный заряд электронного газа компенсируют друг друга.

Поместим металлический проводник во внешнее электрическое поле или сообщим ему какой-нибудь заряд. В обоих случаях на заряды действует электрическое поле, и смещает свободные электроны против поля. Такое движение электронов (ток) приводит к перераспределению зарядов и наступлению равновесия. Этот процесс практически занимает доли секунды. Силы обращаются в ноль, следовательно, внутри проводника Е=0, и силовые линии не проникают внутрь проводника. Следовательно, поток вектора напряженности через любую замкнутую поверхность внутри проводника равен нулю. Из теоремы Гаусса следует, что суммарный заряд внутри проводника также равен нулю, и в статическом случае некомпенсированные заряды распределяются по поверхности проводника. Отсутствие поля внутри проводника означает, что проводник является эквипотенциальным телом: во всех его точках внутри и на поверхности j = const. Силовые линии суммарного поля прерываются на поверхности проводника, и перпендикулярны поверхности. В противном случае составляющая поля, параллельная поверхности, вызвала бы движение зарядов, а это противоречит условию равновесия.

На рис. 41-а[27] изображен проводник, которому сообщили избыточный положи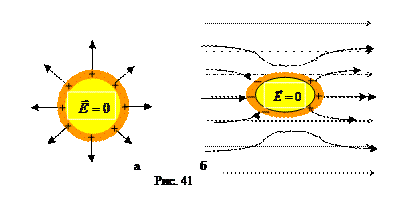тельный заряд, и этот заряд распределился в тонком поверхностном слое, создав вне проводника свое электрическое поле. На рис.41 – б в однородное электрическое поле (его силовые линии показаны тонкими пунктирными линиями) внесли незаряженный металлический проводник. Смещение свободных электронов против поля привело к возникновению на одной стороне поверхности нескомпенсированного отрицательного заряда, а на противоположной стороне – равного ему по величине положительного. Эти заряды называются индуцированными, а физическое явление их возникновения называется электростатической индукцией. Суммарное поле, разумеется, отличается от исходного. На рисунке его силовые линии изображены черными сплошными линиями. Если помещенный в поле проводник разделить на две части (левую и правую на нашем рисунке) и разъединить их, то получим два разноименно заряженных тела, даже если их удалить их внешнего поля.

4. Рассмотрим, как распределяются заряды по поверхности проводника в зависимости от ее формы. Пусть имеются два заряженных шарообразных (сферических) проводника разных радиусов, расстояние между которыми достаточно велико, чтобы можно было считать их уединенными заряженными сферами. Напомним, что заряженная сфера создает электрическое поле вне своего объема, причем, такое же, какое создает точечный заряд, равный заряду сферы и помещенный в ее центр, так что потенциал поверхности сферы j =q/ 4p e₀r=s S/ 4p e₀r=s r/e₀. Здесь s - поверхностная плотность заряда, S= 4p r² – площадь сферы. Соединим заряженные сферы тонким проводником, и получим единый проводник. Заряды перераспределятся на его поверхности в соответствии с условиями равновесия. Учитывая, что потенциалы во всех точках проводника внутри и на поверхности одинаковы, получили, что s r= const. Это значит, что поверхностная плотность заряда обратно пропорциональна радиусу кривизны поверхности. Особенно велика концентрация зарядов на остриях. Поэтому напряженность поля вблизи острия может быть такой большой, что возникает ионизация молекул воздуха вблизи него. Ионы противоположного знака, нежели заряд острия, притягиваются к нему и уменьшают заряд острия. Ионы одного знака с зарядом острия отталкиваются от него и увлекают за собой нейтральные молекулы газа. Возникает «электрический ветер», создающий эффект стекания заряда с острия.[28] Свойство зарядов концентрироваться на острие объясняет, почему во время грозы молния чаще всего ударяет в высокие деревья и в высокие постройки. Это свойство используют на практике, в частности, при устройстве громоотводов (точнее, молниеотводов).

5. Еще раз подчеркнем свойства электростатического поля в веществе:

· В электростатическом поле диэлектрик поляризуется и ослабляет поле.

· Электростатическое поле не проникает внутрь проводника. Если надо уберечь от воздействия внешнего электростатического поля какое-либо устройство, достаточно окружить его проводящим экраном (металлической сеткой). На практике такие экраны используют для электростатической защиты.

§ 7.7. Электроемкость. Конденсатор.

1. При сообщении проводнику избыточного электрического заряда он распределяется по поверхности проводника соответствии с ее формой. При наступлении равновесия проводник становится эквипотенциальным телом. Если проводнику сообщить дополнительный заряд, то он распределится подобно предыдущему, и поверхностная плотность заряда в каждой точке пропорционально увеличится. Соответственно увеличится созданное этими зарядами электрическое поле, так что j ~ q, и коэффициент пропорциональности является индивидуальной характеристикой проводника. Эта характеристика называется электрической емкостью (электроемкостью) проводника. Ее обозначают С. По определению

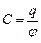(7.7.1)

Емкость уединенного проводника зависит от его геометрии (формы и размеров) и от диэлектрических свойств окружающей среды. Покажем это на примере уединенного шара (сферы). Для него j=q/ 4p e₀er, и электроемкость сферы

С= 4p e₀er (7.7.2)

В СИ единица измерения емкости называется фарад (Ф): 1Ф=1Кл/1В. Это довольно крупная единица измерения. Например, шар размером с Землю (радиус земли около 6400 км) имеет емкость С =4p^.8,85^.10^-12 6,4^.10⁶@0,7^.10^-3Ф=700 мкФ. На практике обычно используют дольные единицы: мФ, мкФ, пФ.

При приближении к заряженному проводнику другого незаряженного проводника на втором проводнике появятся индуцированные заряды, причем, заряды разноименного с первым проводником знака расположатся ближе к нему, нежели одноименные. Электрическое поле индуцированных зарядов складывается с полем заряженного проводника. Разноименные с зарядом первого проводника индуцированные заряды уменьшают его поле, одноименные увеличивают. Влияние разноименных сильнее – они ближе расположены к первому проводнику. В итоге потенциал первого проводника уменьшается, тогда как его заряд на изменяется, что означает увеличение емкости первого проводника. Таким образом, емкость проводника зависит не только от его геометрии, но и от окружающих его тел.

2. Электрический конденсатор представляет собой устройство для накопления электрического заряда и энергии электрического поля. Он состоит из двух изолированных проводников, заряженных разноименными зарядами одинаковой величины. Проводники называются обкладками конденсатора. Им придают такую форму, чтобы электрическое поле локализовалось в пространстве между обкладками. Его силовые линии выходят из одной обкладки и входят в другую. Наиболее распространены конденсаторы плоские, сферические и цилиндрические. Их обкладками являются соответственно две параллельных плоскости, две концентрические сферы разных радиусов и два соосных цилиндра разных радиусов.

Электроемкость конденсатора

С=q/U (7.7.3)

Здесь q - заряд конденсатора, он численно равен заряду каждой его пластины: q= q ₊=| q _-ç. U – напряжение на конденсаторе, оно равно разности потенциалов его обкладок U = j₊ -j_-.

Рассмотрим плоский конденсатор с площадью пластин S и расстоянием между пластинами d. Если расстояние между пластинами мало по сравнению с линейными размерами пластин, то поле такого конденсатора можно считать однородным (см. §7.3 пример в). Его напряженность E=s / e₀e. Напряжение на конденсаторе U=Еd==sd / e₀e.. Учитывая, что s = q/d, получаем формулу емкости плоского конденсатора:

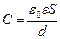(7.7.4)

3. При параллельном соединении конденсаторов их одноименно заряженные пластины соединяются между собой (рис. 42 а). Заряд батареи конденсаторов складывается из зарядов отдельных конденсаторов, напряжение на батарее и на каждом конденсаторе одно и то же, и емкости складываются:

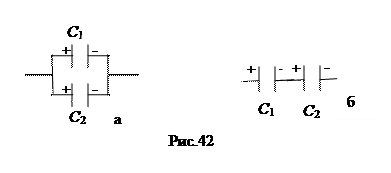С= S С_i (7.7.5)

При последовательном соединении конденсаторов (рис. 42 б) заряд батареи и каждого конденсатора один и тот же, напряжение батарей равно сумме напряжений на конденсаторах, и складываются обратные величины емкостей:

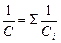(7.7.6)

Получите самостоятельно формулы (7.7.5) и (7.7.6).

§ 7.8. Энергия электрического поля.

1. Рассмотрим процесс зарядки конденсатора. Он связан с перемещением свободных электронов с одной обкладки на другую. Обкладка, с которой забирают свободные электроны, приобретает избыточный положительный заряд. Другая обкладка, куда добавляются свободные электроны, заряжается отрицательно. Уже первая порция заряда создает в конденсаторе электрическое поле, и перенос каждой новой порции заряда происходит против действующих на них сил. Работа этих сил отрицательная: dA=-Udq, и она идет на приращение потенциальной энергии зарядов в электростатическом поле: dW=Udq. Пользуясь формулой dq=CdU, получаем dW=UCdU. Интегрируя это выражение, находим: 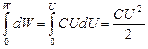. Учитывая, что q=CU, получаем формулы энергии заряженного конденсатора:

Дата добавления: 2014-01-06