Физические теории 3 страница

Для упругой деформации за нулевой уровень потенциальной энергии естественно принять недеформированное состояние, тогда формула потенциальной энергии упруго деформированного тела имеет вид:

Е_п=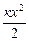 (2.4.6)

5. Полная механическая энергия тела Е (иногда ее называют механической энергией) состоит из кинетической и потенциальной энергий:

Е = Е_к + Е_п (2.4.7)

§ 2.5. Краткие итоги главы 2

• Динамическая характеристика тела (м.т.) – масса m.
• Характеристика внешнего воздействия – сила .
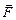• Уравнение движения м.т. – второй закон Ньютона.
• Динамические характеристики состояния м. т. – импульс 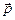, энергия Е.
• Алгоритм решения задачи динамики:
1. Выбрать систему отсчета, связать с ней систему координат, нарисовать тело (м.т.)
2. Нарисовать векторы сил, заменив ими воздействие на рассматриваемое тело окружающих тел.
3. Записать векторное уравнение движения.
4. Записать уравнение движения в проекциях на координатные оси, решить их.

Глава 3.Законы сохранения в механике.

§ 3.1.Фундаментальный характер законов сохранения

1. Законы сохранения утверждают, что некая физическая величина, характеризующая состояние физической системы, остается неизменной (сохраняется) при изменении состояния системы. В механике выполняются законы сохранения импульса, энергии и момента импульса. Содержание закона сохранения момента импульса подробно обсудим в следующей главе. Законы сохранения, как и принцип относительности (см. § 1.1), выделяются среди законов физики своей всеобщностью, фундаментальностью. Они выполняются для нерелятивистских и релятивистских движений в классической и в квантовой физике. Например, законы Ньютона, рассмотренные в предыдущей главе, выполняются только для нерелятивистских классических частиц.

2. Принцип относительности и законы сохранения вначале были получены экспериментально как обобщение опыта. Позднее, по мере развития научных знаний, стало понятно, что происхождение законов сохранения связано со свойствами симметрии природы, которые проявляются в однородности и изотропности пространства и однородности времени.

Однородность пространства, т.е. эквивалентность всех его точек, проявляется в том, что любое физическое явление, наблюдающееся в некоторой точке пространства, в точности повторится в любой другой точке при совпадении внешних условий. Именно однородность пространства обеспечивает воспроизводимость результатов одинаковых экспериментов, проведенных в разных лабораториях. На практике, оборудование, изготовленное в одном месте, нормально работает в любом другом месте при соблюдении условий эксплуатации. Однородность пространства приводит к закону сохранения импульса.

Однородность времени проявляется в физической эквивалентности разных его моментов и приводит к закону сохранения энергии.

Свойство изотропности пространства есть физическая эквивалентность разных направлений в пространстве: если не нарушены внешние условия (условия эксплуатации), то поворот установки не повлияет на результаты ее работы. Изотропность пространства приводит к закону сохранения момента импульса.

Подчеркнем, что в законах сохранения проявляются свойства симметрии пространства и времени, а не симметрии физических тел (например, симметрия кристаллов).

§ 3.2. Закон сохранения импульса.

1. Совокупность тел, взаимодействующих только между собой, образует замкнутую систему тел. Взаимодействие между телами создает внутренние силы, внешние силы отсутствуют. Импульс 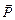системы n тел равен векторной сумме импульсов всех тел системы:

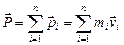(3.2.1)

2. Пусть замкнутая система состоит из двух взаимодействующих тел. Импульс каждого тела вследствие взаимодействия изменяется согласно второму закону Ньютона: 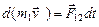, 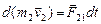. Учитывая, что силы взаимодействия подчиняются третьему закону Ньютона (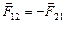), получаем: 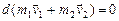, т.е. 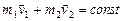. Полученный результат показывает, что импульс каждого тела в замкнутой системе вследствие взаимодействия может изменяться, но так, что их сумма остается неизменной. Этот результат легко обобщить не произвольное число тел замкнутой системы. Импульс замкнутой системы тел сохраняется – это формулировка закона сохранения импульса. В классической механике он имеет вид:

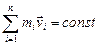(3.2.2)

Напомним, что одному векторному уравнению в трехмерной декартовой системе координат соответствуют три скалярных. Если на систему тел действуют внешние силы, но в некотором направлении система замкнута и внешние силы отсутствуют, то в этом направлении сохраняется ее импульс. На практике немало тому примеров: отдача при стрельбе, реактивное движение и т.п.

3. В классической механике законы Ньютона и закон сохранения импульса выражают одни и те же свойства окружающего мира, однако, как мы обсуждали в предыдущем параграфе, закон сохранения импульса имеет более широкую область применения и выполняется для квантовых систем.

4. Импульс тела имеет вышедшее из употребления, но более точно отражающее его физический смысл название – количество движения, т.е. «запас движения». Закон сохранения импульса является законом сохранения «запаса движения». Действительно, из практики мы знаем, что перекладывание, например, денег из одного кармана в другой или раскладывание их по разным карманам не изменяет их сумму. Об этом же говорит арифметическое правило: от перемены мест слагаемых сумма не изменяется. Природа едина, и ее законы универсальны.

§ 3.3. Закон сохранения механической энергии

1. Пусть тело (м.т.) движется под действием консервативной силы. Ее работа превращается в приращение кинетической энергии тела (см. формулу 2.4.3): 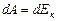и происходит за счет уменьшения потенциальной энергии (см. формулу 2.4.4): 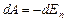. Отсюда следует: 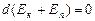, т.е. полная механическая энергия тела сохраняется. Совокупность сил, действующих на тело в каждой точке пространства, образует поле сил. Поле консервативных сил называется потенциальным силовым полем. Закон сохранения энергии для тела в потенциальном силовом поле имеет вид:

Е=Е_к+Е_п=const (3.3.1)

Примеры действия этого закона на практике нам хорошо известны. Мячик, выпущенный из рук, падая под действием силы тяжести, ускоряется, и его потенциальная энергия превращается в кинетическую. Ударившись о пол, мячик отскакивает и, замедляясь, движется вверх – его кинетическая энергия переходит в потенциальную. Если бы не было неконсервативной силы сопротивления воздуха, то идеально упругий мячик поднялся бы на исходную высоту, а затем его падения и подскоки продолжались бы бесконечно долго.

2. Закон сохранения механической энергии можно обобщить на замкнутую систему тел, взаимодействующих между собой консервативными силами. При этом полная механическая энергия системы складывается из кинетических энергий отдельных тел и потенциальная энергия взаимодействия всех тел системы, зависящей от их взаимного расположения.

3. Если на систему тел действуют внешние силы, или внутри нее есть неконсервативные силы, то их работа изменяет механическую энергию. Например, работа силы трения всегда отрицательна, в результате механическая энергия уменьшается, расходуется на работу сил трения. В этом случае можно говорить о законе изменения механической энергии

DЕ=Е₂ –Е₁=А (3.3.2)

Он утверждает, что изменение механической энергии незамкнутой неконсервативной системы тел, равное разности ее конечного и начального значений, равно работе внешних и неконсервативных сил. Формула (3.3.2) имеет большое практическое значение. Рассмотрим, например, как скорость влияет на длину тормозного пути: DЕ = mv²/ 2, А=F_трS, так что при увеличении скорости в 2 раза тормозной путь увеличивается в 4 раза.

4. Помимо механической энергии существуют другие формы энергии, связанные с другими видами движения материи: тепловая, электрическая и т.д., которые могут превращаться друга в друга в эквивалентных количествах. С учетом разных форм энергии закон сохранения энергии приобретает всеобщий характер и превращается в один из наиболее общих законов физики: он утверждает количественную неизменность энергии замкнутой системы при качественном изменении формы энергии при изменении формы движения.

§ 3.4. Столкновения тел

1. Столкновением (ударом) называется процесс, когда тела, первоначально удаленные друг от друга так, что их взаимодействием можно пренебречь, сближаются и непродолжительное время энергично взаимодействуют друг с другом. После удара взаимодействие тел прекращается. Столкновения подразделяются на упругие и неупругие. Как правило, силы, действующие во время удара, изменяются довольно сложным и не всегда известным образом, поэтому решить уравнения движения непросто. Но если речь ведется не о процессе взаимодействия, а об его результате, то законы сохранения легко дают ответ на этот вопрос. Изменение скоростей сталкивающихся тел происходит в результате их взаимодействия друг с другом, поэтому система тел является замкнутой, и ее импульс сохраняется. При упругом ударе внутренние силы консервативные, так что в этом случае выполняется закон сохранения механической энергии.

2. Упругий удар. При столкновении упругие тела деформируются, возникающие при этом упругие силы уменьшают скорость их относительного движения до нуля, превращая кинетическую энергию относительного движения в потенциальную энергию упругой деформации. В следующий момент упругие силы начинают расталкивать тела, у них опять появляется и растет скорость относительного движения вплоть до момента исчезновения деформаций. К этому времени тела опять движутся независимо друг от друга каждое со своей скоростью. После упругого удара внутренние состояния и формы тел (если нельзя пренебречь их размерами) не изменяются. Рассматриваемые тела образуют замкнутую консервативную систему, в ней выполняются законы сохранения импульса и механической энергии:

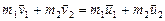(3.4.1)

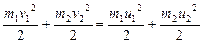(3.4.2)

Здесь индексы 1 и 2 указывают номера тел, v и u – скорости тел соответственно до и после удара. В начальный момент тела еще не столкнулись, в конечный момент столкновение уже закончилось, и механическая энергия состоит только из кинетической энергии, потенциальная энергия взаимодействия отсутствует. Система из двух уравнений позволяет найти две неизвестных величины, например, скорости обоих тел после упругого удара. Рассмотрим некоторые частные случаи.

а) Движущееся тело стакивается с покоящимся, массы тел одинаковы. Законы сохранения примут вид: 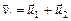; v₁²=u₁²+ u₂². Обратите внимание: один вектор равен сумме двух других (вспомните правило треугольника), и для этого треугольника выполняется теорема Пифагора. Вывод: после такого удара тела разлетаются под прямым углом. Такую ситуацию можно встретить на биллиардном столе, если удар не крученый.

б) Центральный удар. Удар шаров называется центральным, если их скорости до удара направлены по одной прямой, проходящей через их центры, и вращение шаров отсутствует. Такой удар может произойти, когда шары движутся навстречу друг другу, или один шар догоняет другого. После удара скорости по-прежнему направлены вдоль той же прямой, что до удара, и векторное уравнение закона сохранения импульса (3.4.1) превращается в скалярное:

m₁v₁+m₂v₂=m₁u₁+m₂u₂. (3.4.3)

Направление скоростей тел учитывается знаком: изменение направления движения отражается в изменении знака скорости на противоположный. Формула (3.4.2) закона сохранения энергии останется неизменной. Перепишем формулы (3.4.3) и (3.4.2) так:

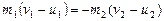(3.4.4)

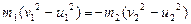(3.4.5)

Преобразуем эту систему из двух уравнений с двумя неизвестными, причем, первое оставим без изменения, а другое получим, поделив (3.4.5) на (3.4.4):

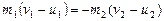
v₁+ u₁ = v₂+ u₂

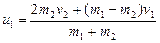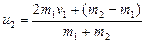Результат решения: и . Обратите внимание на симметрию полученных формул: замена индекса 1 на индекс 2 превращает одну формулу в другую. Заметим, что это следствие симметрии уравнений системы относительно замены индекса.

Проверим полученные результаты на простом примере, который хорошо известен из опыта: движущийся биллиардный шар ударяет покоящийся, удар центральный. Наши формулы дают ожидаемый результат: шары обменяются скоростями – первый остановится, зато второй начнет двигаться.

3. Неупругий удар. После столкновения тела движутся с одинаковыми скоростями 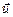, «сцепившись» друг с другом, но суммарный импульс сохранится – система замкнутая:

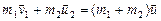(3.4.6)

При центральном неупругом ударе уравнение закона сохранения импульса превратится из векторного в скалярное:

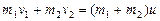(3.4.7)

Система тел неконсервативная, в ней действуют неупругие силы, работа которых частично превращает механическую энергию в тепло: .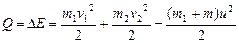

Потери механической энергии зависят от соотношения масс тел и их скоростей. Если движущееся тело неупруго сталкивается с покоящимся, то доля потерь механической энергии зависит только от соотношения их масс. Выведите формулу, какая доля механической энергии в этом случае превращается в тепло, и проанализируйте ее для двух случаев неупругого удара: забивание гвоздя или ковка детали. Тогда станет понятнее, почему молоток должен быть значительно массивней гвоздя, а наковальня значительно массивней детали.

Глава 4. Динамика вращательного движения.

§ 4.1. Кинетическая энергия вращающегося и катящегося тел

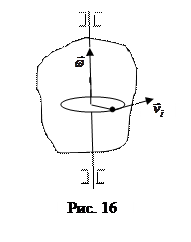
1. Найдем кинетическую энергию тела, вращающегося относительно неподвижной оси. Используем модель а.т.т. как сумму м.т. (рис.16). Все точки тела движутся по окружностям, траектория одной из них массой m_i, движущейся по окружности радиусом r_i со скоростью υ_i. указана на рисунке. Кинетическая энергия этой точки 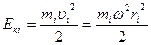. Найдем кинетическую энергию тела как сумму кинетических энергий образующих его точек: 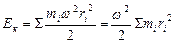. Полученный результат показывает, что кинетическая энергия вращающегося тела определяется двумя величинами: его угловой скоростью и еще одной индивидуальной характеристикой тела, зависящей от распределения его массы относительно оси вращения: 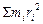. Ее называют моментом инерции тела относительно оси:

I = S m_ir_i² (4.1.1)

Формула кинетической энергии вращающегося тела имеет вид:

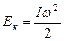(4.1.2)

2. В § 1.4 мы отмечали, что произвольное движение твердого тела можно представить как сумму двух движений: поступательного и вращательного. На практике часто встречается качение твердого тела – это вид плоского движения, т.е. такого движения, когда все точки тела перемещаются в параллельных плоскостях. Кинетическая энергия катящегося тела складывается из двух частей:

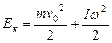(4.1.3)

Здесь v₀ - скорость поступательного движения центра инерции, I₀ – момент инерции тела относительно оси, проходящей через центр инерции тела перпендикулярно плоскостям перемещения его точек.

§ 4.2. Момент инерции

1. Из формул (4.1.2) и (4.1.3) следует, что момент инерции тела при вращательном движении является аналогом массы при его поступательном движении, а именно, служит мерой инертности тела, т.е. его способности сопротивляться изменению скорости: чем больше инертность тела, тем труднее изменить его скорость. Из определения момента инерции (см. формулу 4.1.1) следует, что инертность тела при вращении зависит от распределения его массы относительно оси вращения. Это означает, что одно и то же тело относительно разных осей вращения имеет разные моменты инерции. Это нам хорошо известно из опыта: чем дальше вращающаяся масса от оси вращения, тем труднее ускорить или замедлить ее вращение. Момент инерции, как и масса, скалярная величина, его единица измерения в СИ обозначается кг^.м².

Для сплошного однородного тела, рассматриваемого как совокупность м.т., с точки зрения математики удобно суммирование свести к интегрированию. Пусть dm – масса физически малого элемента объема dV [3], находящегося на расстоянии r от оси вращения, плотность вещества тела - r (кг/м³), тогда dm=r dV, и момент инерции этого элемента массы dI = r²dm = r²r dV. Формула для вычисления момента инерции сплошного тела примет вид:

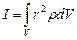(4.2.1)

Интегрирование проводят по всему объему тела, это обозначено ниже знака интеграла.

2. Приведем формулы моментов инерции некоторых тел, часто встречающихся в практике.

а) Обруч или тонкостенный цилиндр массой m и радиусом R, вращающийся относительно своей оси симметрии. Учитывая, что все элементы массы Dm находятся на одинаковом расстоянии от оси, получаем по формуле (4.1.1):

I = S m_ir_i² = R² S m_i = m R² (4.2.2)

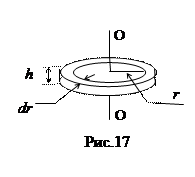б) Диск или сплошной цилиндр массой m и радиусом R, вращающийся относительно своей оси симметрии. Используем формулу (4.2.1), для этого диск разобьем на кольцевые слои. Один такой слой толщиной dr, высотой диска h и объемом dV= 2p rhdr показан на рис. 17. Момент инерции такого элементарного слоя в виде кольца dI= r²r dV= r²r 2p rhdr= 2p rhr³dr. Заметим, что в этом примере интегрирование по объему тела свелось к интегрированию по расстоянию r от оси до внешней поверхности цилиндра, так что 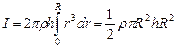. Учитывая, что объем цилиндра V=Sh=pR²h, а его масса m=rV, получили:

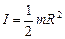(4.2.3)

Используя изложенный в этой главе материал, объясните, одновременно ли достигнут конца спуска два цилиндра одинаковых размеров, если один из них сплошной, а другой пустотелый, и они одновременно начали скатываться с вершины наклонной плоскости (вспомните лекционную демонстрацию).

в) Шар, вращающийся относительно своей оси (эту формулу нетрудно получить интегрированием, перейдя в сферическую систему координат):

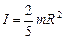(4.2.4)

г) Стержень длиной l, вращающийся относительно перпендикулярной к нему оси, проходящей через его середину (получите эту формулу самостоятельно):

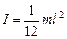(4.2.5)

д) Теорема Штейнера позволяет найти момент инерции тела относительно любой оси, если известен его момент инерции относительно параллельной оси, проходящей через центр инерции тела:

I=I₀+mb² (4.2.6)

Здесь I – момент инерции тела относительно рассматриваемой оси, I₀ - момент инерции этого же тела относительно оси, проходящей через центр инерции и параллельной рассматриваемой, b – расстояние между этими осями. Обратите внимание, что момент инерции тела относительно любых параллельных осей наименьший в случае, когда ось проходит через центр инерции. Самостоятельно получите формулу для момента инерции стержня, если ось вращения проходит через его конец и перпендикулярна стержню.

§ 4.3. Работа и мощность при вращательном движении. Момент силы относительно оси

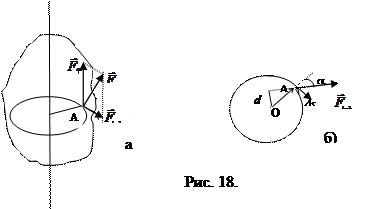
1. Тело может вращаться вокруг неподвижной оси. В точке А (рис.18 - а) к нему приложена сила 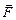. При вращении тела точка А описывает окружность радиусом r. Найдем работу силы, для чего разложим ее на две составляющие: одна параллельна оси вращения - 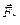, а другая лежит в плоскости, перпендикулярной оси вращения - 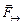. Очевидно, что 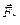не участвует во вращении тела. Она перпендикулярна перемещению, и ее работа равна нулю. Составляющая 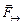лежит в плоскости траектории, описываемой точкой А (рис. 18-б), и образует угол a с радиусом окружности. Перемещение Ds направлено по касательной к траектории. Напомним, что касательная и радиус окружности взаимно перпендикулярны. Элементарная работа силы (см. формулу 2.4.2) dA=F_^ ds sin rdj. [4]. Учитывая, что ds = rdj, где dj -угловое перемещение тела, а rsina=d (см. рис 18-б). d – это длина перпендикуляра, опущенного из оси вращения (точка О) на линию действия силы F_^, называется плечом силы. Итак, dA=F_^d^.dj. Первые два сомножителя в этой формуле определяются силой и тем, где и как она приложена к телу. Их произведение называется моментом силы относительно оси:

M = F_^d (4.3.1)

Заметим, что при вращательном движении тела мерой внешнего воздействия на него служит момент силы.

2. Формула работы при вращении тела под действием момента силы из начального положения с угловой координатой j₁ в конечное положение с угловой координатой j₂ принимает вид:

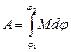(4.3.2)

Для постоянного момента силы:

A=MDj (4.3.3)

Мощность при вращении:

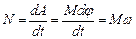(4.3.4)

3. Подробнее рассмотрим физический смысл характеристики внешнего воздействия на тело, имеющего ось вращения. Она называется моментом силы относительно оси. Представьте себе, что Вы хотите открыть дверь, прикладывая силу к ручке двери. Если эта сила параллельна оси или лежит в плоскости двери, то она не сдвинет дверь с места. Вы хорошо представляете, как надо приложить силу, чтобы получить нужный результат. Наибольшее воздействие оказывает сила, перпендикулярная плоскости двери. Если такую же силу приложить в точке, находящейся ближе к оси вращения, то эффект ее воздействия уменьшится. Таким образом, внешнее воздействие на вращающееся тело зависит не только от величины силы, но и от точки ее приложения и от направления по отношению к оси вращения. Совокупность этих факторов отражается в определении момента силы относительно оси вращения (формула 4.3.1): M = F_^d. Итак, мерой внешнего воздействия на вращающееся тело является момент силы. Его единица измерения в СИ называется ньютон-метр и обозначается Н^.м.

Рассматривая кинематику вращательного движения (§ 1.4), мы встретились с аксиальными (осевыми) векторами: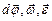. Момент силы относительно оси также аксиальный вектор: он направлен по оси вращения в соответствии с правилом правого винта. Посмотрите на рис.18 и определите направление вектора 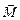: вниз по оси на рис.а) и перпендикулярно плоскости рисунка от нас на рис. б). На рис. 18-б) изображена траектория точки приложения силы при вращении тела - окружность радиуса r. Задав положение этой точки вектором 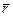, модуль которого равен радиусу окружности, получаем векторную формулу:

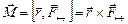(4.3.5)[5]

Самостоятельно убедитесь, что модуль вектора момента силы выражается уже знакомой нам формулой (4.3.1).

§ 4.4. Уравнение динамики вращательного движения.

1. Еще раз напомним, что уравнение динамики (его также называют основным законом динамики) позволяет рассчитать закон движения тела, если известно оказываемое на него внешнее воздействие и начальное состояние. Уравнением динамики поступательного движения (или м.т.) является второй закон Ньютона (§ 2.2). Получим аналогичный физический закон для вращательного движения.

2. Пусть а.т.т. вращается под действием внешней силы. Ее работа на элементарном перемещении dA=Mdj идет на приращение кинетической энергии тела dE=d (Iw²/ 2), его потенциальная энергия измениться не может – тело не изменяет свою высоту над землей и не деформируется. Для а.т.т. момент инерции I=const, так что dE=Iwdw. Учитывая, что dA= dE, получаем: Mdj =Iwdw. Поделим обе части полученного уравнения на рассматриваемый промежуток времени dt, и, используя формулы кинематики dj/dt =w, dw /dt =e, получаем:

Ie =M (4.4.1)

Эта формула выражает уравнение динамики вращательного движения или, его другое название, основной закон динамики вращательного движения. Он, как и уравнение динамики поступательного движения, констатирует, что причиной изменения скорости служит внешнее воздействие. Этому же закону можно придать другой вид: 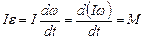, откуда следует:

d(Iw)=Mdt (4.4.2)

Mdt называют импульсом момента силы.

3. Уравнение динамики вращательного движения (4.4.1) применимо и тогда, когда на тело действует несколько моментов сил. В этом случае ускорение определяет их равнодействующая. Учитывая, что угловое ускорение и момент силы относительно оси – аксиальные векторы, запишем основной закон динамики в векторной форме:

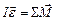(4.4.3)

Еще раз обсудим, почему формула (4.4.3) есть уравнение динамики вращательного движения. Знание моментов сил позволяет найти угловое ускорение, которое, по определению, есть вторая производная по времени от закона движения. Таким образом, уравнение (4.4.3) есть дифференциальное уравнение второго порядка. Дважды проинтегрировав это уравнение и зная начальное состояние тела (его местоположение и скорость в начальный момент времени), получим полную информацию о состоянии тела в любой момент времени.

§ 4.5. Закон сохранения момента импульса

1. Движущееся тело сразу остановиться не может, время торможения зависит от интенсивности внешнего воздействия и от «запаса движения». Для материальной точки или поступательно движущегося тела «запас движения» измеряется импульсом 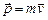. При вращении тела его «запас движения» также зависит от инертности тела и его скорости и называется моментом импульса:

Дата добавления: 2014-01-06